[color=var(--content-color)]

[color=var(--content-color)]只有一个分类型自变量X和一个因变量Y的方差分析称为单因素方差分析，例如要检验四种饲料喂猪对猪体重增加值的均值是否相等，只涉及“饲料类型”一个类别因子，这就是单因素方差分析。从[color=var(--dui-color-purple-p9)]试验设计的角度，一般采用的是完全随机设计。

[color=var(--content-color)]一、分析思路

[color=var(--content-color)]单因素方差分析思路如图 4‑8所示。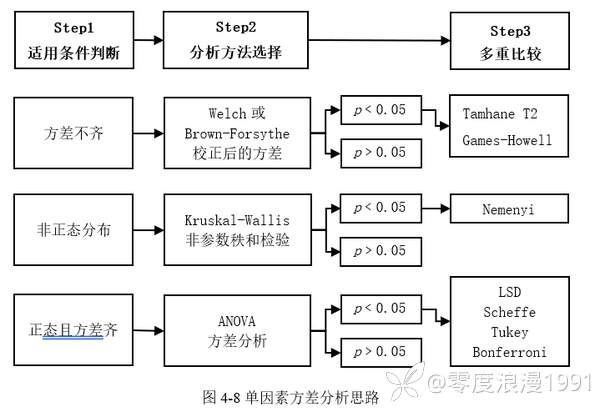

[color=var(--content-color)](1) 适用条件判断

[color=var(--content-color)]一般在单因素方差分析前，应检验各组数据是否满足正态性要求，以及是否满足[color=var(--dui-color-purple-p9)]方差齐性要求。

[color=var(--content-color)](2) 分析方法选择

[color=var(--content-color)]根据上一步正态性和方差齐性检验的结果，选择合适的分析方法。如果同时满足正态性与方差齐性，则进行单因素方差分析；如果方差不齐，可选择Welch或Brown-Forsythe检验对方差分析结果进行校正；如果数据[color=var(--dui-color-purple-p9)]非正态分布，则考虑转换数据使得满足正态性或当严重偏态时考虑采用Kruskal-Wallis[color=var(--dui-color-purple-p9)]秩和检验作为替代分析方法。

[color=var(--content-color)]方差分析、Welch以及Kruskal-Wallis秩和检验在结果解释和分析时，当检验的概率p值小于0.05时，认为差异显著或因素对因变量的影响有统计学意义；反之p值大于0.05时，因子的影响无意义。

[color=var(--content-color)](3) 多重比较

[color=var(--content-color)]方差分析单因素[color=var(--dui-color-purple-p9)]主效应结果有显著性后，根据具体情况选择合适的多重比较方法进行组间的两两比较。常见的多重比较方法比如LSD、Scheffe、Tukey、Bonferroni、Sidak等可用于方差齐性的情形。当方差不齐时，可使用Tamhane T2、Games-Howell等方法。如果采用了Kruskal-Wallis秩和检验，可采用Nemenyi法进行多重比较。

[color=var(--content-color)]二、实例分析

[color=var(--content-color)]【例4-7】研究显示DON([color=var(--dui-color-purple-p9)]脱氧雪腐镰刀菌烯醇)可能对幼鼠关节软骨代谢产生影响。将30只健康幼鼠完全随机分配至对照组、DON低剂量组和[color=var(--dui-color-purple-p9)]高剂量组，每组10只。高、低剂量组分别给予0.25μg/g、0.06μg/g的DON，对照组给予相同容量生理盐水灌胃，连续80天后免疫组法检测小鼠软骨内Ⅱ型胶原含量，含量降低提示关节软骨损伤。实验结果数据见表 4‑13，试分析DON对关节软骨代谢是否存在影响。案例数据来源于李晓松(2017)，并对数据有修改编辑，数据文档见“例4-7.xls”。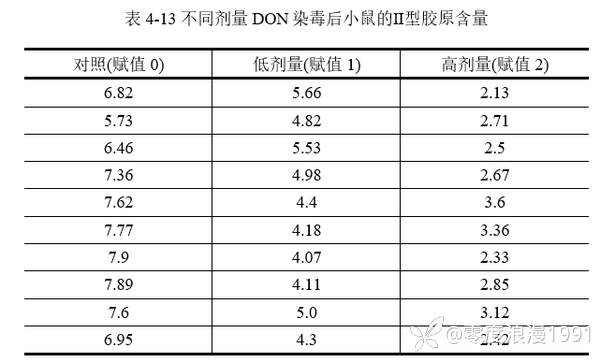

[color=var(--content-color)](1) 数据与[color=var(--dui-color-purple-p9)]案例分析

[color=var(--content-color)]数据文档中的“group”为分组组别，编码0表示对照组，编码1表示DON[color=var(--dui-color-purple-p9)]低剂量组，编码2表示DON高剂量组。本例为完全随机设计，多组均值的差异比较应考虑使用单因素方差分析。

[color=var(--content-color)](2) 正态性与方差齐性条件判断

[color=var(--content-color)]通过【通用方法】→【正态性检验】模块进行[color=var(--dui-color-purple-p9)]正态检验，三组胶原含量数据服从整体分布(均p﹥0.05)。通过【通用方法】→【方差】→【方差齐检验】模块进行方差齐性检验，F=1.16，p=0.329﹥0.05，说明数据满足方差齐性要求，结果见表 4‑14。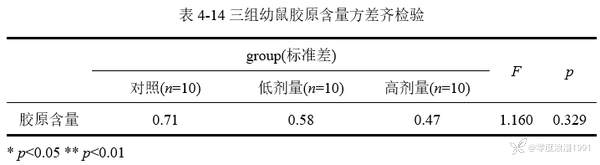

[color=var(--content-color)]本例数据满足正态性、方差齐性要求，根据上述分析思路，接下来进行单因素方差分析。

[color=var(--content-color)](3) 单因素方差分析

[color=var(--content-color)]依次选择【通用方法】→【方差】模块。将[color=var(--dui-color-purple-p9)]组别变量“group”拖拽至右侧【X(定类)】框内，因变量“胶原含量”拖拽至右侧【Y(定量)】框内。复选框框内选择【方差分析】，操作界面见图 4‑9，最后单击【开始分析】。

[color=var(--content-color)]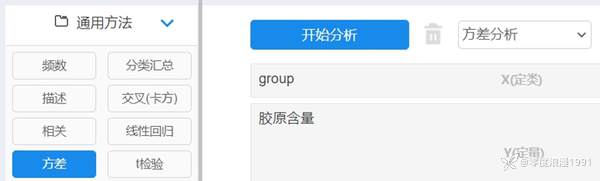

[color=var(--content-color)]表 4‑15为常规的[color=var(--dui-color-purple-p9)]方差分析表，其中平方和、自由度、均方为F检验中间计算的过程值，通常可不做解读分析，主要关注的结果是F[color=var(--dui-color-purple-p9)]统计量值与显著性p值。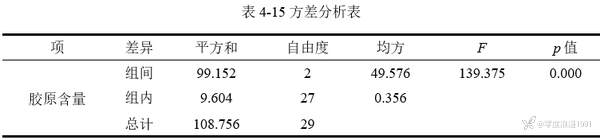

[color=var(--content-color)]在科研写作时，常见用于结果报告的表格，如表 4‑16所示。

[color=var(--content-color)]三组胶原含量依次为：对照组(7.21±0.71)μg/g、DON低剂量组(4.71±0.58)μg/g、DON高剂量组(2.77±0.47)μg/g。方差分析结果显示，F=139.375，p﹤0.01，在α=0.01水平下，表明不同剂量DON分组的胶原含量差异具有统计学意义，或者说DON不同剂量对[color=var(--dui-color-purple-p9)]关节软骨损伤有影响。

[color=var(--content-color)](4) 多重比较

[color=var(--content-color)]单因素方差分析在主效应显著的前提下，即当F检验的p值小于0.05时应继续考察因素各水平之间对因变量影响的差异，可以通过【事后多重比较】模块完成。

[color=var(--content-color)]依次选择【进阶方法】→【事后多重比较】。将组别自变量“group”拖拽至右侧【X(定类)】框内，因变量“胶原含量”拖拽至右侧【Y(定量)】框内。本例[color=var(--dui-color-purple-p9)]多重比较方法选项框选择【Bonferroni校正】，同时勾选【字母标记法】。如果在研究中还需要报告多重比较结果的[color=var(--dui-color-purple-p9)]效应量，可勾选【效应量】选项，平台将输出Cohens´d值效应量，一般可根据研究需要进行输出和解释分析，本例不做选择。操作界面见图 4‑10，最后单击【开始分析】。

[color=var(--content-color)]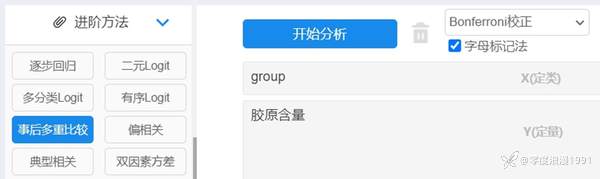

[color=var(--content-color)]【事后多重比较】模块输出的结果比较丰富，包括了方差分析以及多重比较结果。此处主要介绍多重比较，见表 4‑17。

[color=var(--content-color)]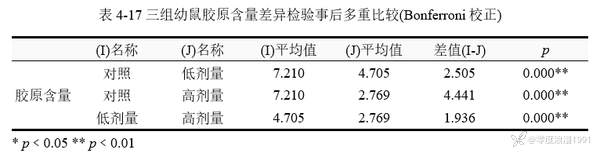

[color=var(--content-color)]高剂量组的胶原含量显著低于其他两组(Bonferroni p﹤0.01)，低剂量组的胶原含量也显著低于对照组(Bonferroni p﹤0.01)。

[color=var(--content-color)]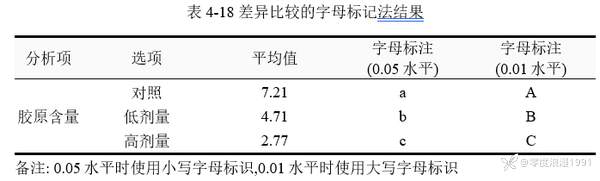

[color=var(--content-color)]幼鼠胶原含量两两组间差异比较的字母标记结果见表 4‑18，上表中包括显著性水平α=0.05和α=0.01两个标准的字母标记。各水平字母相同则表示差异不显著，字母不同则表示差异有统计学意义。例如在α=0.05水平下，对照组标记字母a，而其他两组标记字母b和c，三个不同字母即表明对照、低剂量组、高剂量组的胶原含量两两之间的差异有统计学意义。

[color=var(--content-color)]以上内容摘自《SPSSAU科研数据分析方法与应用》第4章——差异关系研究，书中不仅涵盖了数据清理、统计分析和模型构建等内容，还提供了丰富的案例，以便于读者在实际研究中应用。