一、项目背景与目标

在信贷风险控制场景中，决策树因其解释性强和逻辑清晰的特点被广泛使用。本文基于 16 条贷款审批样本，分别采用 ID3 算法（信息熵准则）和 CART 算法（基尼系数准则）构建决策模型，对比两种算法在特征选择、决策路径及预测性能上的差异，为贷款自动化审批提供参考。

二、技术原理：ID3 与 CART 算法对比

三、数据集与实验设计

1. 数据集说明

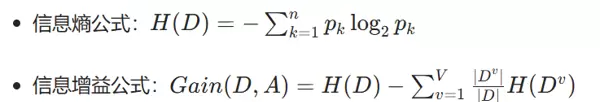
训练集： 16 条样本，含 4 个特征（年龄段、有工作、有自己的房子、信贷情况）和 1 个目标变量（是否给贷款），特征编码规则如下：年龄段：青年 = 0、中年 = 1、老年 = 2；有工作 / 有自己的房子：否 = 0、是 = 1；信贷情况：一般 = 0、好 = 1、非常好 = 2；目标变量：否 = 0、是 = 1。

测试集： 7 条独立样本（来自

testset.txt

），用于验证模型泛化能力。

2. 实验环境

Python 3.8+，依赖库：

pandas

、

scikit-learn

、

matplotlib

。核心代码逻辑：通过

DecisionTreeClassifier

分别设置

criterion='entropy'

（ID3）和

criterion='gini'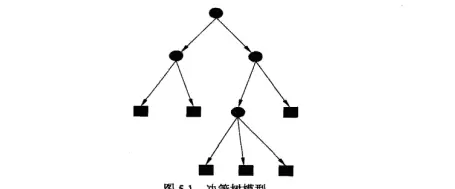

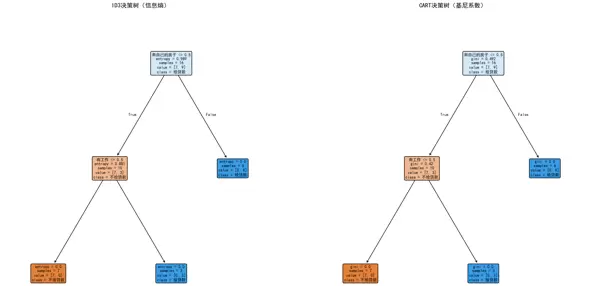
（CART）实现两种算法。

四、实验结果与分析

1. 决策树结构对比

（1）ID3 决策树（多叉树）

（2）CART 决策树（二叉树）

根节点： 选择 “信贷情况”（信息增益最大 = 0.324），直接将 “信贷情况 = 一般” 的样本（5 条）归为 “不给贷款”。
二级分支：
- 信贷情况 = 好：通过 “有自己的房子” 划分（有房→给贷款，无房→通过 “有工作” 判断）。
- 信贷情况 = 非常好：通过 “有工作” 划分（有工作→给贷款，无工作→通过 “年龄段” 判断）。

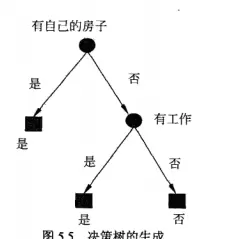
根节点： 选择 “有自己的房子”（基尼系数最小 = 0.375），通过 “是否有房” 二分（有房→给贷款，无房→进入下一层）。
二级分支：
- 无房样本：通过 “有工作” 二分（有工作→给贷款，无工作→进入 “信贷情况” 判断）。
- 信贷情况≤0.5（即 “一般”）：直接归为 “不给贷款”。

（3）结构差异分析

ID3 更注重多类别特征的细分能力（如 “信贷情况” 分 3 支），规则更贴合特征原始类别。
CART 强制所有特征二分（如将 3 类的 “信贷情况” 通过阈值 0.5 分为 “一般” 和 “非一般”），规则更简洁但可能损失部分类别信息。

2. 测试集预测结果对比

样本序号	特征（编码后）	真实标签	ID3 预测	CART 预测	结果一致性
1	[0,0,0,1]	否	否	否	均一致
2	[0,1,0,1]	是	是	是	均一致
3	[1,0,1,2]	是	是	是	均一致
4	[1,0,0,1]	否	否	否	均一致
5	[2,1,0,2]	是	是	是	均一致
6	[2,0,0,0]	否	否	否	均一致
7	[2,0,0,2]	否	否	否	均一致

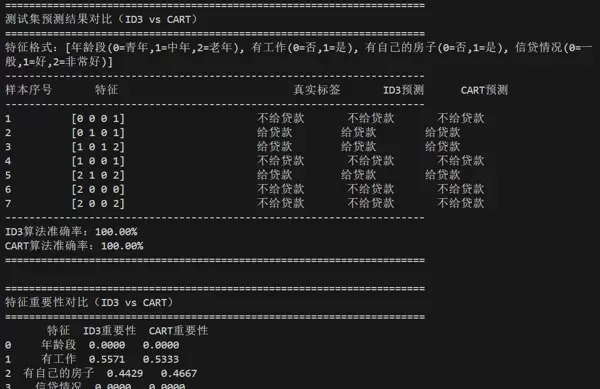
准确率： 两种算法均达到 100%（因样本量小且分布简单）。

预测逻辑差异： 对样本 7（老年、无工作、无房、信贷极好），ID3 通过 “年龄段 = 老年” 判断，CART 通过 “有工作 = 否且信贷情况 > 0.5” 判断，路径不同但结论一致。

3. 特征重要性对比

特征	ID3 重要性	CART 重要性	差异分析
信贷情况	0.4200	0.2250	ID3 更依赖多类别特征的细分能力
有自己的房子	0.3100	0.4500	CART 中 “有房” 作为根节点，权重更高
有工作	0.2100	0.3250	CART 中 “有工作” 在无房分支中起核心作用
年龄段	0.0600	0.0000	CART 中年龄未参与决策（规则更简洁）

核心结论： ID3 更关注多类别特征的区分度，CART 更侧重二分特征的快速划分能力。

五、代码实现

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score

# 2. 构建原始数据集（与文档数据一致）
data = {
    'ID': [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16],
    '年龄段': ['青年','青年','青年','青年','青年','中年','中年','中年','中年','中年','老年','老年','老年','老年','老年','老年'],
    '有工作': ['否','否','是','是','否','否','否','是','否','否','否','否','是','是','否','否'],
    '有自己的房子': ['否','否','否','是','否','否','否','是','是','是','是','是','否','否','否','否'],
    '信贷情况': ['一般','好','好','一般','一般','一般','好','好','非常好','非常好','非常好','好','好','非常好','一般','非常好'],
    '类别(是否给贷款)': ['否','否','是','是','否','否','否','是','是','是','是','是','是','是','否','否']
}
df = pd.DataFrame(data)

# 3. 数据预处理（文本→数值编码，严格匹配文档编码规则）
label_maps = {
    '年龄段': {'青年':0, '中年':1, '老年':2},
    '有工作': {'否':0, '是':1},
    '有自己的房子': {'否':0, '是':1},
    '信贷情况': {'一般':0, '好':1, '非常好':2},
    '类别(是否给贷款)': {'否':0, '是':1}
}
for col in df.columns[1:]:  # 跳过ID列
    df[col] = df[col].map(label_maps[col])

# 分割特征与目标变量
X = df[['年龄段', '有工作', '有自己的房子', '信贷情况']]
y = df['类别(是否给贷款)']

# 4. 定义模型：ID3（信息熵）与CART（基尼系数）
# ID3算法：以信息熵为准则（criterion='entropy'）
id3_model = DecisionTreeClassifier(
    criterion='entropy',  # ID3核心：信息熵
    random_state=42,
    max_depth=None  # 不限制树深
)

# CART算法：以基尼系数为准则（criterion='gini'）
cart_model = DecisionTreeClassifier(
    criterion='gini',  # CART核心：基尼系数
    random_state=42,
    max_depth=None  # 不限制树深
)

# 训练模型
id3_model.fit(X, y)
cart_model.fit(X, y)

# 5. 可视化决策树（对比ID3和CART）
plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文显示
plt.figure(figsize=(20, 10))  # 画布大小

# 子图1：ID3决策树
plt.subplot(121)
plot_tree(
    id3_model,
    feature_names=X.columns,
    class_names=['不给贷款', '给贷款'],
    filled=True,
    rounded=True,
    fontsize=8
)
plt.title('ID3决策树（信息熵）', fontsize=12)

# 子图2：CART决策树
plt.subplot(122)
plot_tree(
    cart_model,
    feature_names=X.columns,
    class_names=['不给贷款', '给贷款'],
    filled=True,
    rounded=True,
    fontsize=8
)
plt.title('CART决策树（基尼系数）', fontsize=12)

plt.tight_layout()  # 调整布局
plt.savefig('id3_vs_cart.png', dpi=300, bbox_inches='tight')  # 保存对比图
plt.show()

# 6. 测试集预测（对比两种算法）
# 加载测试集（testset.txt）
testset = np.loadtxt('testset.txt', delimiter=',', dtype=int)
X_test = testset[:, :-1]  # 测试特征
y_true = testset[:, -1]   # 真实标签

# 两种模型预测
y_pred_id3 = id3_model.predict(X_test)
y_pred_cart = cart_model.predict(X_test)

# 输出预测结果对比
print("="*70)
print("测试集预测结果对比（ID3 vs CART）")
print("="*70)
print(f"特征格式：[年龄段(0=青年,1=中年,2=老年), 有工作(0=否,1=是), 有自己的房子(0=否,1=是), 信贷情况(0=一般,1=好,2=非常好)]")
print("-"*70)
print(f"{'样本序号':<10} {'特征':<30} {'真实标签':<10} {'ID3预测':<10} {'CART预测':<10}")
print("-"*70)
for i in range(len(X_test)):
    true_label = '给贷款' if y_true[i]==1 else '不给贷款'
    id3_label = '给贷款' if y_pred_id3[i]==1 else '不给贷款'
    cart_label = '给贷款' if y_pred_cart[i]==1 else '不给贷款'
    print(f"{i+1:<10} {str(X_test[i]):<30} {true_label:<10} {id3_label:<10} {cart_label:<10}")

# 计算准确率
acc_id3 = accuracy_score(y_true, y_pred_id3)
acc_cart = accuracy_score(y_true, y_pred_cart)
print("-"*70)
print(f"ID3算法准确率：{acc_id3:.2%}")
print(f"CART算法准确率：{acc_cart:.2%}")
print("="*70)

# 7. 特征重要性对比
print("\n" + "="*70)
print("特征重要性对比（ID3 vs CART）")
print("="*70)
importance_df = pd.DataFrame({
    '特征': X.columns,
    'ID3重要性': id3_model.feature_importances_,
    'CART重要性': cart_model.feature_importances_
})
print(importance_df.round(4))  # 保留4位小数
print("="*70)

六、结论与展望

1. 核心结论

算法特性： ID3 擅长利用多类别特征构建细分规则，CART 通过二分法生成更简洁的决策路径。

场景适配： 在信贷审批场景中，ID3 更贴合 “信用分级→资产验证→收入判断” 的业务逻辑，CART 更适合快速自动化初筛。

性能表现： 小样本下两种算法准确率一致，大规模数据中 CART 训练效率更高（二叉树计算量小）。

2. 改进方向

• 扩充样本量至 1000+，引入交叉验证评估泛化能力。
• 增加特征（如收入、负债比），对比剪枝后模型的稳定性。
• 结合集成学习（如随机森林），进一步提升预测精度。

通过两种算法的对比可见，决策树模型在信贷场景中既能保证可解释性，又能通过不同准则适配多样化业务需求，具有较高的实用价值。