数据结构

什么是置换选择排序？置换选择排序是用来干啥的？

在数据处理领域，尤其是面对大量无序数据时，如何高效地进行排序成为了一个重要的课题。置换选择排序正是这样一种用于外部排序的技术，其目的是将大量的无序数据转换成有序数据，以便于后续的归并操作。

通常情况下，归并排序涉及将多个已排序的子数组合并成一个更大的有序数组。然而，当我们手头的数据是完全无序的，如何生成这些有序的子数组就成了关键问题。外部排序的基本方法之一是通过逐步合并单个元素开始，逐步形成更大的有序段落，从而构建初始的归并段。

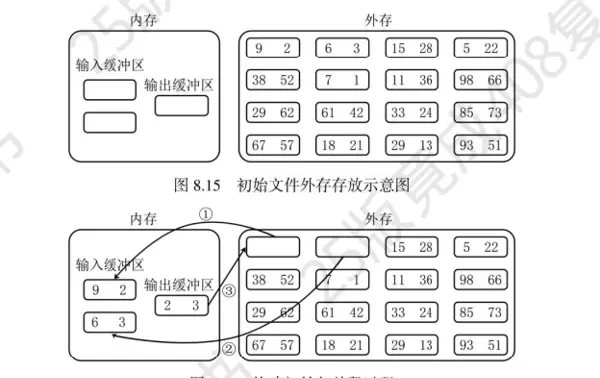
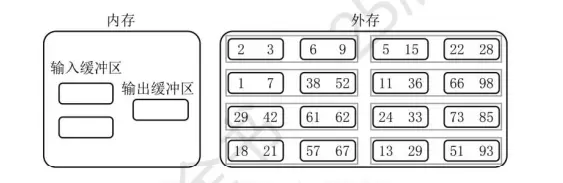
尽管这种方法直观易懂，但它存在明显的缺陷——归并段的数量过多。在外部排序中，每一次归并都会导致大量的I/O操作，这是影响性能的主要因素。为了减少归并过程中的I/O次数，置换选择排序应运而生。该方法通过增加每个归并段的长度，有效减少了所需的归并段数量，从而提高了外部排序的整体效率。

具体来说，置换选择排序通过特定的策略生成更长的归并段，从而减少了归并过程中的I/O操作次数，提高了排序的效率。

什么是最佳归并树？最佳归并树是用来干什么的？

在多路归并过程中，合理地组织归并段可以显著提高排序效率。最佳归并树，即哈夫曼树，是一种用于优化多路归并过程的树形结构。当需要将多个有序段合并成一个更大的有序数组时，尤其是在受限于系统资源（如只能支持有限路数的归并）的情况下，最佳归并树可以帮助我们找到最优的归并策略。

例如，假设我们有四个长度分别为2、3、5、100的有序归并段，需要将它们合并成一个大的有序数组，但系统仅支持三路归并。在这种情况下，我们需要通过多次三路归并来完成任务。不同的归并策略会导致不同的总比较次数，而我们的目标是找到一种策略，使总比较次数最少。

根据三路归并的比较次数公式：总比较次数 = (总元素数 - 1) × (k - 1)，其中k表示归并的路数。通过构建哈夫曼树，我们可以确保每次归并的比较次数最小化，从而优化整个归并过程。

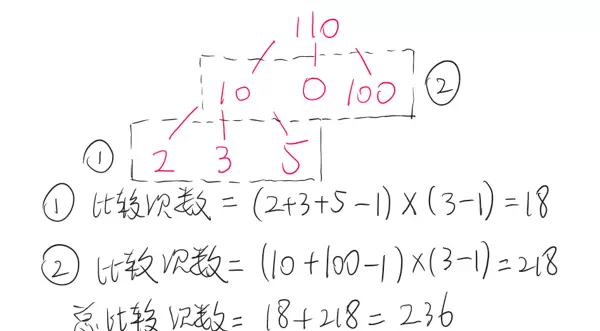
哈夫曼树通过最小化加权路径长度（WPL）来实现这一目标，即使得归并过程中所有元素的比较次数之和最小。为了确保构建的哈夫曼树具有最小的WPL，有时需要添加虚拟的0节点，以确保树的结构符合要求。

什么是败者树？败者树是用来干什么的？

败者树是一种用于优化多路归并过程中每轮比较次数的数据结构。在多路归并中，通常需要从多个有序子序列中选择最小的元素。传统的做法是使用for循环遍历所有子序列的首元素，时间复杂度为O(n)。而败者树通过构建一棵特殊的树形结构，可以在O(log n)的时间内完成这一操作，大大提高了效率。

例如，假设有4个有序子序列，每个子序列都是递增的。通过败者树，我们可以快速地从这4个子序列中选出最小的元素，然后将其加入到最终的有序序列中，同时更新败者树，以准备下一次的选择。

什么是十字链表？什么是多重邻接表？二者有啥区别？

十字链表和多重邻接表是两种用于存储稀疏矩阵或图的数据结构，它们各有特点，适用于不同的应用场景。

十字链表： 十字链表是一种用于存储稀疏矩阵的数据结构。每个非零元素由一个节点表示，每个节点包含行指针、列指针、值以及指向同一行和同一列的下一个非零元素的指针。这种结构使得在稀疏矩阵中查找、插入和删除非零元素变得非常高效。

多重邻接表： 多重邻接表主要用于图的存储。每个顶点有一个邻接表，记录与其相邻的所有顶点。此外，每个边还包含一个额外的指针，指向与该边关联的另一个顶点的相同边。这种结构使得在图中查找和操作边变得更为方便。

两者的区别在于：
- 应用范围： 十字链表主要用于稀疏矩阵的存储，而多重邻接表主要用于图的存储。
- 节点信息： 十字链表的节点包含行指针和列指针，而多重邻接表的节点包含邻接顶点的信息和指向另一端点的指针。
- 操作效率： 十字链表在稀疏矩阵的操作中更为高效，而多重邻接表在图的边操作中更为高效。

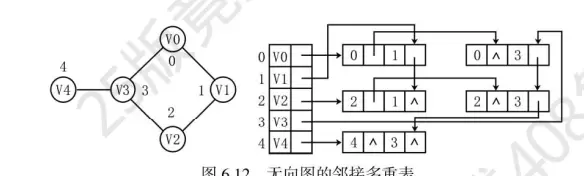
图这种数据结构的基本存储方式主要包括邻接矩阵和邻接表两种。此外，十字链表和多重邻接表可以视为邻接表的变化形式，前者适用于有向图，后者则用于无向图。

十字链表详解

十字链表的头部节点由三个字段构成：

• data: 保存与顶点相关的资料。
• firstIn: 指向入边列表中的首个边节点。
• firstOut: 指向出边列表中的首个边节点。

而十字链表的边节点则由四至五个字段构成：

• tailVex: 表示弧尾（即边的起点）在顶点列表中的索引，对应于邻接矩阵元素 edges[i][j] 中的行索引 i。
• headVex: 表示弧头（即边的终点）在顶点列表中的索引，对应于邻接矩阵元素 edges[i][j] 中的列索引 j。
• hLink: 指向弧头为顶点 headVex 的下一条边，即邻接矩阵中该列的下一个元素。
• tLink: 指向弧尾为顶点 tailVex 的下一条边，即邻接矩阵中该行的下一个元素。
• info (可选): 可选字段，用于存储边的相关信息，如在加权有向图中，info 可存放边的权重。

多重邻接表解析

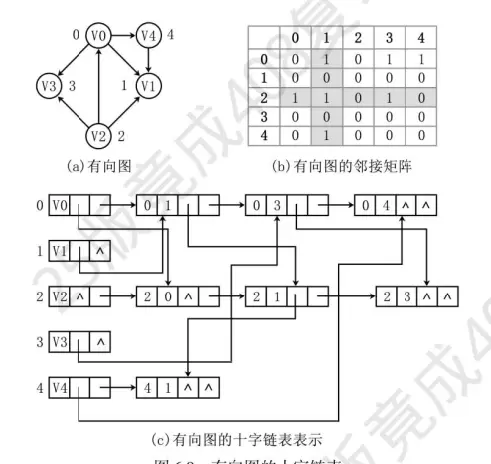
多重邻接表的头部节点由两个字段构成：

• data: 保存顶点的相关信息。
• firstEdge: 指向与该顶点相连的第一条边。

边节点由四到六个字段构成：

• mark (可选): 可选字段，可用于标记该边节点是否已被访问。
• iVer 和 jVer: 分别表示一条边的两个端点在顶点列表（数组）中的索引。
• iLink: 指向与顶点 iVer 相连的下一条边。
• jLink: 指向与顶点 jVer 相连的下一条边。
• info (可选): 可选字段，用于存储边的相关信息，例如在加权有向图中，info 可存放边的权重。

迪杰斯特拉算法概述

迪杰斯特拉算法采用贪婪策略来解决图中单源最短路径的问题。为了更好地理解这一算法，让我们来看一个具体的例子。假设你需要找出图中 V1 顶点到图中其它各个顶点的最短路径。

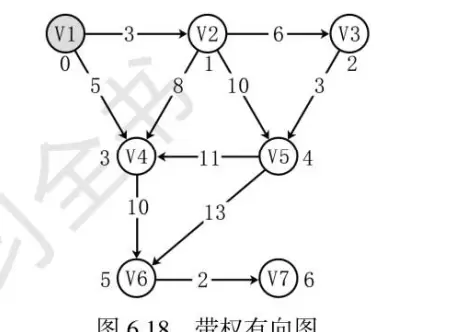
首先，我们找到离 v1 最近的 v2 点，并将其纳入考虑范围。接下来，允许 v1 通过 v2 到达其他节点。再次选择距离 v1 最短的 v4 点（已选过的 v2 不再考虑）。随后，允许 v1 经过 v2 和 v4 到达其他节点，依此类推。

弗洛伊德算法解析

弗洛伊德算法基于动态规划的思想，用于计算图中任意两点之间的最短路径。该算法的核心在于，对于任意两个顶点，存在两种最短路径的可能性：直接从一个顶点到达另一个顶点，或者通过某个中间顶点到达目标顶点。

i

算法的具体步骤如下：

1. 在初始阶段，不允许通过其他节点到达目标节点，只有直接到达或距离为无穷大。
2. 第二轮开始，允许通过顶点 v1 到达其他节点，逐步更新任意两点间最短路径。
3. 第三轮继续，允许通过顶点 v1 和 v2 到达其他节点，持续更新任意两点间的最短路径。
4. 如此循环，直至允许绕过任何一个节点，最终确定两点间最短路径。

动态规划的状态定义为：允许经过前 k 个中间节点时，顶点 i 到顶点 j 的最短路径长度。状态转移方程则基于是否通过第 k 个节点来决定最短路径的选择。

为了减少空间占用，可以将原本的三维数组压缩为二维数组，从而将空间复杂度从 O(n^3) 降低到 O(n^2)。

弗洛伊德算法通常应用于有向图或无向图中所有顶点间的最短路径求解；支持图中包含负权边（但不允许存在负权回路）。该算法更适合顶点数量较少的情况，因为其时间复杂度为 O(n^3)，当 n 较大时，计算效率会显著下降。

j

i

j

k

i → ... → k → ... → j

n

n-1

dp[k][i][j]

dp[k][i][j] = min( dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j] )

dp[k-1][i][j]

dp[k-1][i][k] + dp[k-1][k][j]

O(n?)

dp[k][...]

dp[k-1][...]

dist[i][j]

dist[i][j] = min( dist[i][j], dist[i][k] + dist[k][j] )

n

O(n?)

以下代码实现了弗洛伊德算法，包括路径长度的计算和路径的重建（通过矩阵记录中间节点）：

        INF = float('inf')

        def floyd_warshall(n, edges):
            """
            参数：
            n: 顶点数量（顶点编号0~n-1）
            edges: 边列表，格式为 [(i, j, weight), ...]
            返回：
            dist: 最短路径长度矩阵，dist[i][j]表示从i到j的最短距离
            path: 路径记录矩阵，path[i][j]表示从i到j的最短路径中的中间节点
            """
            # 1. 初始化dist和path矩阵
            dist = [[INF] * n for _ in range(n)]
            path = [[-1] * n for _ in range(n)]  # -1表示没有中间节点

            # 顶点到自身的距离为0
            for i in range(n):
                dist[i][i] = 0

            # 初始化边的权重
            for i, j, w in edges:
                dist[i][j] = w
                path[i][j] = -1  # 直接路径没有中间节点

            # 2. 核心弗洛伊德算法：遍历中间节点k，更新所有i,j
            for k in range(n):
                for i in range(n):
                    for j in range(n):
                        # 如果i→k和k→j可达，且路径更短，则更新
                        if dist[i][k] != INF and dist[k][j] != INF and dist[i][j] > dist[i][k] + dist[k][j]:
                            dist[i][j] = dist[i][k] + dist[k][j]
                            path[i][j] = k  # 记录中间节点k

            return dist, path

        # 3. 路径重建函数（递归）
        def get_path(path, i, j):
            """重建从i到j的最短路径"""
            k = path[i][j]
            if k == -1:  # 没有中间节点，直接返回[i,j]
                return [i, j] if i != j else [i]

            # 递归获取i→k和k→j的路径，合并（去掉重复的k）
            return get_path(path, i, k)[:-1] + get_path(path, k, j)

        # ------------------- 测试 -------------------
        if __name__ == "__main__":
            n = 3  # 3个顶点
            edges = [
                (0, 1, 2),
                (1, 2, 3),
                (0, 2, 5),
                (2, 1, -1)
            ]
            dist, path = floyd_warshall(n, edges)

            # 打印最短路径长度矩阵
            print("最短路径长度矩阵：")
            for row in dist:
                print([f"{x:2d}" if x != INF else "∞" for x in row])

            # 打印具体路径（例如0→2）
            i, j = 0, 2
            print(f"\n{i}到{j}的最短路径：", get_path(path, i, j))
            print(f"{i}到{j}的最短距离：", dist[i][j])
    

path

代码输出结果如下：

最短路径长度矩阵：
['0 ', '2 ', '5 ']
['∞', '0 ', '3 ']
['∞', '-1', '0 ']

0到2的最短路径： [0, 2]
0到2的最短距离： 5

弗洛伊德算法复杂度分析

O(n?)

k

i

j

n

O(n?)

dist

path

n×n

弗洛伊德算法与迪杰斯特拉算法的比较

O(n?)

O(n?)

O(m log n)

m

O(n?)

O(n?)

O(n+m)

n<1000

总结来说，弗洛伊德算法是一种全源最短路径算法，特别适用于小规模图场景，也适用于需要考虑负权边的情况；而当图的规模较大或仅需单源路径时，推荐使用迪杰斯特拉算法。

对于大规模图，且仅需单源路径，同时图中存在负权边的情况，建议使用贝尔曼-福特算法（支持负权边的单源算法）。