一、算法原理与核心流程
BP神经网络架构说明:
- 输入层:接收故障特征数据,例如振动频谱、电流时域参数等维度信息。
- 隐藏层:一般设置为1到3层,每层节点数量建议为输入层节点数的1.5至2倍,以平衡模型复杂度与学习能力。
- 输出层:根据任务类型选择激活函数——Softmax适用于多分类问题,Sigmoid则用于二分类场景。
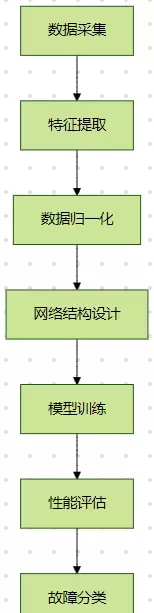
主要运行流程如下图所示:
二、实现代码详解
%% 清除工作空间
clear; clc; warning off;
%% 加载电机故障数据集
load('fault_data.mat'); % 数据包含特征矩阵X和标签向量Y
%% 数据预处理阶段
% 划分训练集(70%)、验证集(15%)和测试集(15%)
cv = cvpartition(size(X,1),'HoldOut',0.3);
X_train = X(training(cv),:);
Y_train = Y(training(cv),:);
X_val = X(test(cv),:);
Y_val = Y(test(cv),:);
% 对特征进行归一化处理
[X_train,norm_params] = mapminmax(X_train',0,1);
X_val = mapminmax('apply',X_val',norm_params);
X_test = mapminmax('apply',X_test',norm_params);
% 将类别标签转换为独热编码格式
Y_train = ind2vec(Y_train');
Y_val = ind2vec(Y_val');
Y_test = ind2vec(Y_test');
%% 构建前馈神经网络结构
input_neurons = size(X_train,2); % 输入层节点数量
hidden_neurons = 12; % 隐藏层节点数(经验取值:约2倍输入维数)
output_neurons = size(Y_train,2); % 输出层节点数由类别总数决定
net = feedforwardnet(hidden_neurons, 'traingdx'); % 使用带动量项的梯度下降法
net.trainParam.epochs = 1000; % 最大训练轮次
net.trainParam.goal = 1e-5; % 设定收敛目标误差
net.trainParam.lr = 0.01; % 学习率设定
net.trainParam.showWindow = 0; % 关闭可视化训练窗口
%% 模型训练执行
[net,tr] = train(net,X_train',Y_train');
%% 性能评估与结果分析
% 在测试集上进行预测
Y_pred = net(X_test');
[~,Y_pred_class] = max(Y_pred);
[~,Y_test_class] = max(Y_test);
% 计算混淆矩阵并统计准确率
C = confusionmat(Y_test_class,Y_pred_class);
accuracy = sum(diag(C))/sum(C(:));
disp(['分类准确率: ', num2str(accuracy*100, '%.2f'), '%']);
% 绘制混淆矩阵图像
figure;
plotconfusion(Y_test_class,Y_pred_class);
title('混淆矩阵分析');
%% 可选:误差分布可视化
figure;
ploterrhist(Y_test_class - Y_pred_class);
title('分类误差分布');
xlabel('预测误差'); ylabel('频数');
三、参数调优策略
1. 网络结构优化方法
- 隐藏层设计:通过交叉验证方式确定最优节点数量,常见范围在8至20之间。
- 激活函数配置:
- 隐藏层推荐使用 tansig 函数提升非线性表达能力。
- 输出层根据分类任务选择 softmax 或 sigmoid。
2. 训练参数调整建议
| 参数名称 |
推荐取值范围 |
优化方法 |
| 学习率 (lr) |
0.001 - 0.1 |
采用自适应学习率算法(如 traingda) |
| 动量因子 (mc) |
0.5 - 0.9 |
使用动量梯度下降(traingdm)加速收敛 |
| 正则化系数 |
0.0001 - 0.01 |
引入 L2 正则化防止过拟合现象 |
3. 正则化技术实现方式
net.performFcn = 'mse'; % 定义性能函数为均方误差
net.performParam.regularization = 0.001; % 设置正则化强度
四、典型问题及应对方案
1. 过拟合现象处理
2. 收敛速度缓慢的改进措施
- 调整学习率至合适区间,避免过大或过小。
- 引入动量项提高梯度下降稳定性。
- 确保输入数据已完成标准化处理,消除量纲影响。
- 尝试更换训练函数,如使用 'trainlm' 或 'traingdx' 提升效率。
采用Levenberg-Marquardt算法进行训练,可通过以下方式设置网络参数:
net = feedforwardnet(hidden_neurons, 'trainlm');
该方法结合特征工程、神经网络结构优化及正则化手段,在确保分类精度的基础上有效增强了模型的泛化性能。
在实际故障诊断应用中,应依据具体的故障类别对隐藏层神经元数量、训练函数等超参数进行适当调整。推荐融合专业领域知识,开展合理的特征选取与模型评估工作。
参考示例代码实现了基于BP神经网络的故障数据分类任务,并可在MATLAB环境中完成建模与仿真分析。

 扫码加好友,拉您进群
扫码加好友,拉您进群