基于MATLAB的PID闭环控制系统设计

本设计涵盖完整的系统设计报告与仿真程序，构建了一个由控制器、测量元件及变送器、执行器（调节阀）以及调节对象（被控过程）组成的单回路闭环负反馈控制系统。该结构在自动化控制领域中具有基础性地位，广泛应用于各类工业过程控制场景。

系统结构解析

此闭环控制系统可视为一个协同运作的整体机制。其中，控制（调节）器扮演核心角色，依据来自测量元件和变送器的反馈信号，实时计算并输出控制指令至执行机构——即调节阀。调节阀据此对被控过程施加影响，从而实现对系统输出的精确调控。

整个回路通过持续比较设定值与实际测量值之间的偏差，并利用PID算法进行动态修正，确保系统响应快速、稳定且误差最小化。这种负反馈机制是保证控制精度和鲁棒性的关键所在。

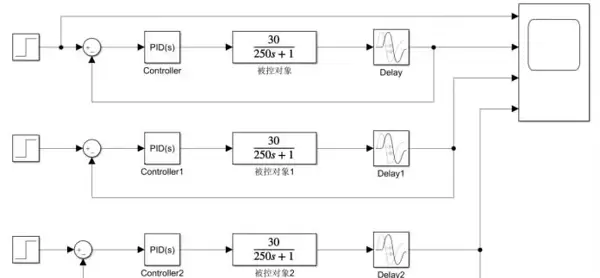
PID控制原理与MATLAB实现

为了直观展示PID控制的工作流程，以下提供一段典型的MATLAB仿真代码示例，用于模拟系统在给定输入下的动态响应过程。

% 定义系统参数
Kp = 2; % 比例系数
Ki = 0.5; % 积分系数
Kd = 0.1; % 微分系数
t = 0:0.01:10; % 时间向量，从0到10秒，步长0.01秒
setpoint = ones(size(t)); % 设定值，这里设为常数1

% 初始化变量
error = zeros(size(t));
integral = 0;
derivative = 0;
output = zeros(size(t));

for i = 2:length(t)
    error(i) = setpoint(i) - output(i - 1); % 计算误差
    integral = integral + error(i) * 0.01; % 积分项，这里简单的用误差和时间步长累积
    derivative = (error(i) - error(i - 1)) / 0.01; % 微分项，用前后误差差除以时间步长近似
    output(i) = Kp * error(i) + Ki * integral + Kd * derivative; % PID控制律计算输出
end

% 绘图
figure;
plot(t, setpoint, 'r--', 'LineWidth', 1.5); hold on;
plot(t, output, 'b', 'LineWidth', 1.5);
xlabel('Time (s)');
ylabel('Output');
legend('Setpoint', 'PID Output');
grid on;

参数定义与作用分析

在代码实现中，首先设定PID控制器的三个核心参数：

• 比例系数

  Kp

  ：负责对当前误差做出即时响应，提升系统的反应速度，使输出迅速趋近目标值；
• 积分系数

  Ki

  ：通过对误差的累积作用，有效消除稳态偏差，提高控制精度；
• 微分系数

  Kd

  ：根据误差变化率进行预判性调节，抑制超调，增强系统稳定性。

仿真设置与变量初始化

时间向量由

t

setpoint

• 误差变量

  error

• 积分项

  integral

• 微分项

  derivative

• 系统输出

  output

控制循环与结果可视化

在主循环中，程序逐时刻更新误差值，累加积分项，计算微分变化，并结合PID公式生成控制输出。最终通过绘图函数将设定值与实际输出随时间的变化曲线绘制出来，便于观察系统的动态性能，如上升时间、超调量、调节时间等指标。

借助MATLAB强大的数值计算与图形显示能力，用户可以高效地搭建模型、调试参数、验证控制策略的有效性。在实际工程应用中，可根据具体被控对象特性反复优化PID参数，以达到最佳控制效果。

本文旨在帮助读者深入理解基于MATLAB平台的PID闭环控制系统的设计思路与实现方法，掌握从理论建模到仿真验证的完整流程。