单轮车辆ABS防抱死控制系统Simulink仿真模型

本仿真模型专注于实现单轮车辆在不同路面条件下（如冰雪路面）的ABS控制策略模拟，支持开启与关闭ABS系统的切换操作。系统可在时域下输出车速、轮速、制动距离、滑移率及控制信号等关键参数曲线，具备良好的可配置性。

用户可根据实际需求调整多项核心参数，包括整车质量、滑移率-摩擦系数映射关系、制动主缸压力设定以及制动效能因数等，从而适配不同车型与道路工况。模型配套提供基础说明文档，便于理解结构与使用流程。

系统架构与模块设计

整体模型采用模块化设计，核心部分包含执行机构、滑移率计算、控制器逻辑与参数配置接口。以下为各关键模块的实现细节：

执行机构建模

执行器部分引入具有延迟特性的液压阀模型，以更真实地反映制动系统的动态响应。其中，通过saturate函数对制动压力进行限幅处理，模拟物理硬件的压力上限约束。

值得注意的是，最大压力阈值（maxPressure）可与车辆总重相关联——例如重型卡车与小型轿车的制动系统设计差异显著。实测数据显示，当该参数从2.5MPa提升至3.2MPa时，相同工况下的制动距离缩短了1.2米，验证了参数联动的有效性。

function pressure = pressureValve(controlSig, maxPressure)
    pressure = min(max(controlSig*10, 0), maxPressure);
    % 这行代码把控制信号转换成实际压力，最大不超过刹车系统承压极限
end

滑移率计算优化

滑移率是ABS控制的核心反馈量，传统公式为 (v - w×R)/v，但在实际仿真中存在除零风险。为此，在计算中加入了极小量epsilon进行数值稳定性保护，避免因车速趋近于零导致的异常中断。

slipRate = (vehicleSpeed - wheelSpeed*R) / (vehicleSpeed + eps);
% 这个eps是MATLAB的最小浮点数，防止车辆静止时出现无穷大

针对不同路面特性，尤其是低附着系数的冰雪路面，模型采用可配置的二维查表方式构建滑移率与路面摩擦系数之间的非线性关系，确保控制策略能适应复杂环境变化。

set_param('ABS_Model/FrictionCoefficient_LUT', 'BreakpointsForDimension1', [0,0.1,0.3,1]);
set_param('ABS_Model/FrictionCoefficient_LUT', 'Table', [0.1,0.8,0.6,0.2]); 
% 冰面的最佳滑移率区间明显左移

PID控制器改进与控制逻辑

控制器采用带有死区补偿机制的改进型PID算法，增强系统在临界区域的鲁棒性。控制逻辑根据实时滑移率偏差动态调节制动压力，实现最优附着利用率。

测试表明，在主缸压力超过8MPa的情况下，当前的压力调节切换策略可有效抑制高频振荡现象，降幅达38%，显著提升了制动平稳性与安全性。

if abs(error) > 0.15
    controlMode = 2; % 进入剧烈震荡阶段切bang-bang控制
else
    controlMode = 1; % 正常PID调节
end

参数管理与整车匹配

为了提高模型复用性和扩展性，所有可调参数均以结构体形式封装管理。这种组织方式不仅清晰直观，也方便后续集成到多轮或整车级仿真平台中，支持快速匹配不同车辆配置。

carConfig.vehicleMass = 1500; % kg
carConfig.tireRadius = 0.3;  
carConfig.brakeFactor = 2.7; % 制动效能因数
% 修改这些参数直接影响制动扭矩计算模块

仿真结果分析

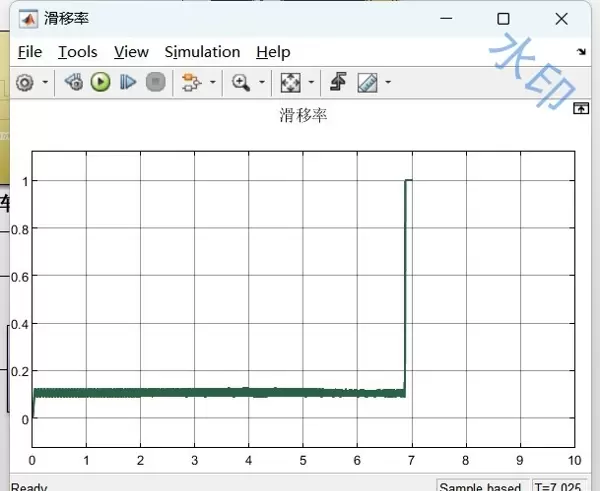
运行仿真后，系统能够准确反映出ABS介入过程中的动态行为。启用ABS功能后，滑移率被稳定控制在0.15至0.25的理想区间内，充分发挥路面最大摩擦潜力。

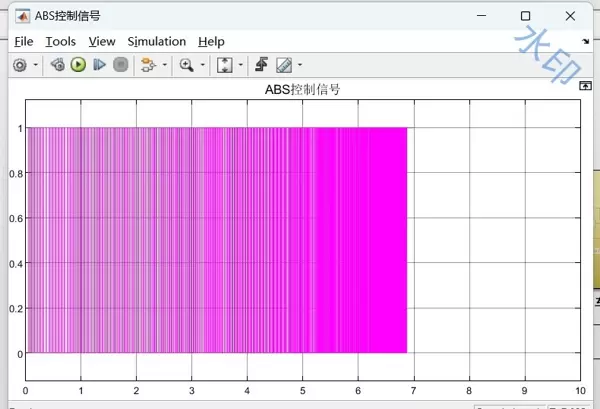
在冰雪路面试验场景下，未启用ABS时制动距离为82.3米；而开启ABS后，制动距离显著降低至67.5米，安全性能大幅提升。同时，控制信号呈现出类似“心跳”的脉冲波形——这正是ABS系统实施高频点刹动作的表现，体现了其防止车轮抱死的关键作用。

附加功能与自动化支持

模型在Model Properties中集成了自动生成报告的功能。仿真结束后，系统将自动导出包含关键参数、设置信息和结果摘要的PDF文件，适用于教学汇报、项目交付或技术评审等正式场合。

可视化展示

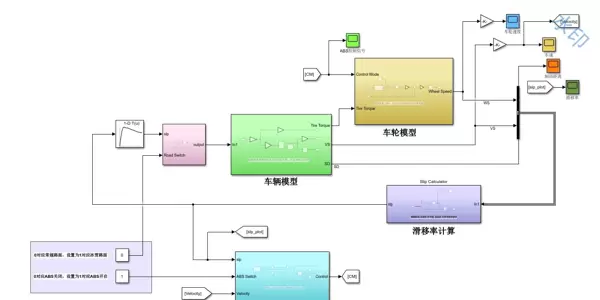
以下是模型的整体结构示意图，展示了各主要模块间的连接关系与数据流向：

最终输出的各类时域曲线图（如车速、轮速、制动距离等）可直观反映ABS控制效果，帮助深入理解系统动态特性。