归并排序算法详解

归并排序（Merge Sort）是一种典型的基于分治策略的高效排序方法，最早由

约翰·冯·诺依曼

于1945年提出。该算法通过“分而治之”的思想，将一个复杂的排序问题逐步拆解为多个更小、更容易处理的子问题，待子问题解决后，再将结果有序地合并起来。

其最显著的优势在于具备稳定的 O(n log n) 时间复杂度，无论在最好、平均还是最坏情况下都能保持高效的运行性能。同时，归并排序是一种稳定排序算法，即相等元素的相对位置不会在排序过程中发生改变，因此被广泛应用于对稳定性有要求的场景中。

核心原理：分解、解决与合并

归并排序的执行过程可归纳为以下三个关键步骤：

• 分解：将原始数组不断递归地划分为两部分，直到每个子数组仅包含单个元素为止。
• 解决：单个元素的数组天然有序，无需进一步操作。
• 合并：将两个已排序的子数组按序合并成一个新的有序数组，此过程持续向上回溯，直至整个数组恢复完整并完全有序。

原始数组: [38, 27, 43, 3, 9, 82, 10]

分解过程:
[38, 27, 43, 3, 9, 82, 10]
        ↓
[38, 27, 43]  [3, 9, 82, 10]
        ↓
[38] [27, 43]  [3, 9] [82, 10]
        ↓
[38] [27] [43] [3] [9] [82] [10]

合并过程:
[27, 38] [43] [3, 9] [10, 82]
        ↓
[27, 38, 43] [3, 9, 10, 82]
        ↓
[3, 9, 10, 27, 38, 43, 82]

逆序对问题及其与归并排序的关系

在许多算法题目中，常会遇到“逆序对”相关的问题。所谓逆序对，指的是数组中满足索引 i < j 且 arr[i] > arr[j] 的元素对 (i, j)。统计此类元素对的数量是常见的任务之一。

若采用暴力枚举所有可能的元素对进行判断，时间复杂度将达到 O(n)，在数据规模较大时效率极低。而借助归并排序的分治结构和合并机制，可以在完成排序的同时高效统计逆序对数量，整体时间复杂度优化至 O(n log n)。

利用归并过程统计逆序对的关键逻辑

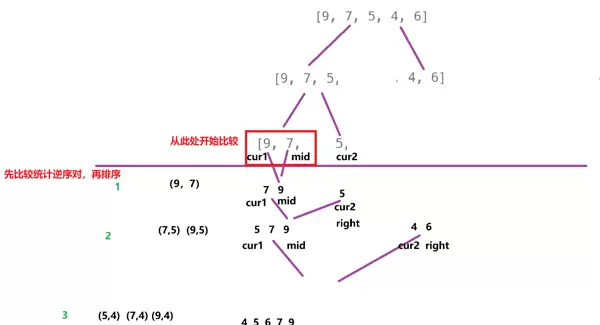
在归并排序的合并阶段，假设左侧子数组 L 和右侧子数组 R 均已按升序排列。当比较 L 中的元素 l_i 与 R 中的 r_j 时，若出现 l_i > r_j，则说明从当前 l_i 开始到 L 末尾的所有元素均大于 r_j（因为 L 本身有序），从而可以一次性累加 mid - cur1 + 1 个逆序对。

这一特性使得在每次合并操作中都能以线性时间 O(n) 完成局部逆序对的统计。结合整体递归深度为 O(log n) 的特点，最终实现总时间复杂度为 O(n log n)，远优于暴力法的 O(N)。

在整个递归划分过程中，每层都将数组分为左右两个区域。在对这两个区域进行排序和合并的同时，实际上也完成了对该区间内逆序对的统计。由于每一层合并时都利用了子数组的有序性，因此能够在线性时间内快速完成计数，极大提升了整体效率。

典型应用题型一：交易逆序对的总数

该问题要求计算数组中所有逆序对的总数。通过改造归并排序的合并逻辑，在合并两个有序子数组的过程中同步统计跨区间的逆序对数量，即可高效求解。

具体实现思路如下：每当左半部分的某个元素大于右半部分的当前元素时，意味着左半部分从该位置到末尾的所有元素都会与右半部分当前元素构成逆序对。利用这一单调性质，可在合并过程中直接累加贡献值。

C++ 实现代码示例

class Solution {
    int tmp[50001]; // 辅助数组，用于归并过程中的临时存储
public:
    int reversePairs(vector<int>& record) {
        // 利用归并排序的思想统计逆序对
        // 排序的同时提升统计效率
        return mergeSort(record, 0, record.size() - 1);
    }

    int mergeSort(vector<int>& nums, int left, int right) {
        if (left >= right) return 0;

        int ret = 0; // 当前递归层级的逆序对数量，避免使用全局变量
        int mid = left + (right - left) / 2;

        // 递归处理左右两部分
        ret += mergeSort(nums, left, mid);
        ret += mergeSort(nums, mid + 1, right);

        // 双指针合并，并统计逆序对
        int cur1 = left, cur2 = mid + 1, i = left;
        while (cur1 <= mid && cur2 <= right) {
            if (nums[cur1] <= nums[cur2]) {
                tmp[i++] = nums[cur1++];
            } else {
                // 出现逆序：左半部分从cur1到mid的所有元素都与nums[cur2]构成逆序对
                ret += mid - cur1 + 1;
                tmp[i++] = nums[cur2++];
            }
        }

        // 处理剩余元素
        while (cur1 <= mid) tmp[i++] = nums[cur1++];
        while (cur2 <= right) tmp[i++] = nums[cur2++];

        // 将排序结果复制回原数组
        for (int j = left; j <= right; ++j) {
            nums[j] = tmp[j];
        }

        return ret;
    }
};

扩展题型：翻转对

“翻转对”是逆序对的一种变体问题，通常定义为满足 i < j 且 nums[i] > 2 * nums[j] 的元素对。虽然条件更为严格，但仍可通过修改归并排序的比较逻辑来高效求解——在合并前先扫描一遍左半部分，统计满足条件的特殊逆序关系，再进行正常归并。

这种基于归并排序框架的拓展方法，体现了分治思想在复杂数组问题中的强大适应能力。

可以沿用翻转对的解题思路。由于条件 i < j 且 nums[i] > 2*nums[j] 的存在，无法在归并排序的合并过程中同时完成统计与合并操作，因此需要先进行翻转对的统计，再执行归并操作。

需要注意的是，在比较时应避免整数溢出问题，建议使用除法或类型转换来处理数值比较。

示例代码如下：

class Solution  
{  
    int tmp[50001];  
public:  
    int reversePairs(vector<int>& nums)  
    {  
        return mergeSort(nums, 0, nums.size() - 1);  
    }  

    int mergeSort(vector<int>& nums, int left, int right)  
    {  
        if (left >= right) return 0;  

        int ret = 0; // 用于记录翻转对的数量  
        int mid = (left + right) >> 1;  

        ret += mergeSort(nums, left, mid);  
        ret += mergeSort(nums, mid + 1, right);  

        int cur1 = left, cur2 = mid + 1, i = left;  

        // 统计阶段：查找满足 nums[i] > 2 * nums[j] 的数量  
        while (cur1 <= mid && cur2 <= right)  
        {  
            if (nums[cur1] / 2.0 > nums[cur2])  
            {  
                ret += mid - cur1 + 1;  
                ++cur2;  
            }  
            else  
            {  
                ++cur1;  
            }  
        }  

        // 归并阶段：将两个有序子数组合并  
        cur1 = left;  
        cur2 = mid + 1;  
        i = left;  

        while (cur1 <= mid && cur2 <= right)  
        {  
            if (nums[cur1] <= nums[cur2])  
                tmp[i++] = nums[cur1++];  
            else  
                tmp[i++] = nums[cur2++];  
        }  

        while (cur1 <= mid)  
            tmp[i++] = nums[cur1++];  

        while (cur2 <= right)  
            tmp[i++] = nums[cur2++];  

        for (int j = left; j <= right; ++j)  
            nums[j] = tmp[j];  

        return ret;  
    }  
};

题目：计算右侧小于当前元素的个数



此问题本质上仍是逆序对的变种。不同之处在于，要求统计每个元素右侧比它小的元素个数，并将结果按原数组中对应位置输出。为了追踪每个元素在排序过程中的原始下标，需引入一个辅助数组 index 来记录元素的初始索引。

在归并排序的过程中，同步维护值数组和下标数组的对应关系。每次将左侧元素加入临时数组时，若其大于右侧某元素，则说明从该位置到右区间末尾的所有元素均构成有效计数，累加至结果数组中对应原始下标的位置。

注意：此处采用降序排列更便于统计右侧较小值的数量。

实现方式如下：



class Solution  
{  
    vector<int> ret;         // 存储最终结果  
    vector<int> index;       // 记录各元素原始下标  
    int numstmp[100001];      // 临时数组，存放排序后的数值  
    int indextmp[100001];     // 临时数组，存放对应的下标  

public:  
    vector<int> countSmaller(vector<int>& nums)  
    {  
        int n = nums.size();  
        ret.resize(n);  
        index.resize(n);  

        for (int i = 0; i < n; ++i)  
        {  
            index[i] = i;  
        }  

        mergerSort(nums, 0, n - 1);  
        return ret;  
    }  

    void mergerSort(vector<int>& nums, int left, int right)  
    {  
        if (left >= right) return;  

        int mid = left + (right - left) / 2;  
        mergerSort(nums, left, mid);  
        mergerSort(nums, mid + 1, right);  

        int cur1 = left, cur2 = mid + 1, i = left;  

        while (cur1 <= mid && cur2 <= right)  
        {  
            if (nums[cur1] <= nums[cur2])  
            {  
                numstmp[i] = nums[cur2];  
                indextmp[i++] = index[cur2++];  
            }  
            else  
            {  
                ret[index[cur1]] += right - cur2 + 1;  
                numstmp[i] = nums[cur1];  
                indextmp[i++] = index[cur1++];  
            }  
        }  

        while (cur1 <= mid)  
        {  
            numstmp[i] = nums[cur1];  
            indextmp[i++] = index[cur1++];  
        }  

        while (cur2 <= right)  
        {  
            numstmp[i] = nums[cur2];  
            indextmp[i++] = index[cur2++];  
        }  

        for (int j = left; j <= right; ++j)  
        {  
            nums[j] = numstmp[j];  
            index[j] = indextmp[j];  
        }  
    }  
};

归并排序是一种解决逆序对问题的高效算法，其核心优势在于利用分治思想与有序子数组合并的过程。在合并两个已排序的子区间时，可以在 O(n) 的时间复杂度内完成逆序对的统计。

通过递归地将数组不断二分，直到每个子段仅含一个元素，再逐步向上合并并统计，最终实现整体的排序与计数。整个过程的时间复杂度为 O(n log n)，虽然需要额外开辟 O(n) 的辅助空间来存储临时数组和索引映射，但相较暴力枚举法在大规模数据下的 O(n) 表现，性能提升显著。

该方法不仅适用于标准逆序对的计算，还可灵活扩展至多种变体问题，例如“右侧小于当前元素的个数”或“翻转对”（即满足 nums[i] > 2×nums[j] 的数对）。在处理这些变体时，关键是在合并阶段调整判断条件，如引入倍率关系进行比较。

实际编码中需注意边界情况的处理，比如左右区间的划分、索引越界检查以及临时数组的正确回填。同时，确保索引数组与原数组同步更新，以准确追踪原始位置的信息。

综上所述，归并排序凭借其稳定的时间效率和良好的可扩展性，成为处理逆序相关问题的首选方案。合理调整合并逻辑后，能够高效应对多种变形题型。