第一章 函数

幂函数

幂函数的一般表达式为：

y = x^μ（其中 μ ∈ ）

其常见的运算性质包括：

• y = x^1/n = √[n]{x}
• y = xⁿ = 1 / xⁿ
• y = xⁿ x^m = x^n+m
• y = (xⁿ)^m = x^mn

以下是一些典型的幂函数及其图像表现：

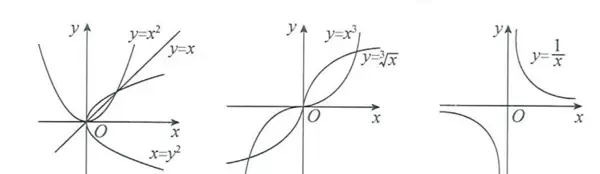
• y = x
• y = x
• y = √x
• y = x
• y = x
• y = 1/x

对数函数

对数函数的标准形式为：

y = log_ax（其中 a > 0 且 a ≠ 1）

定义域与值域：
定义域为 (0, +∞)，值域为 (∞, +∞)

单调性分析：

• 当 a > 1 时，函数 y = log_ax 单调递增。
• 当 0 < a < 1 时，函数 y = log_ax 单调递减。

典型对数函数的图像如下所示：

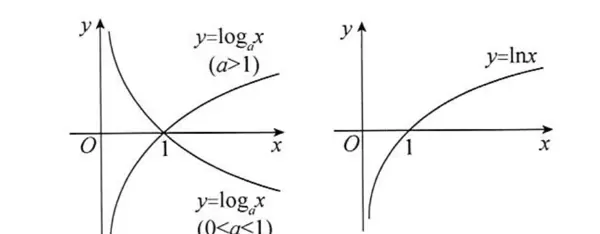
• 函数 y = log_ax（a > 1）呈现单调递增趋势，而 y = log_ax（0 < a < 1）则单调递减，两条曲线均经过点 (1, 0)。
• 自然对数函数 y = lnx 是单调递增的，且通过点 (1, 0)。

极限特性：
当 x 趋向正无穷时，lnx → +∞；
当 x 从右侧趋近于 0 时，lnx → ∞。
即：
lim_x→+∞ lnx = +∞，
lim_x→0 lnx = ∞

特殊取值：
log_a1 = 0，
log_aa = 1，
ln1 = 0，
lne = 1

常用恒等式：

• x = e^lnx（适用于 x > 0）
• u^v = e^vlnu（适用于 u > 0）

三角函数

正弦函数与余弦函数

基本形式为：

y = sinx，y = cosx

定义域和值域：
定义域：(∞, +∞)
值域：[1, 1]

奇偶性特征：

• 正弦函数 y = sinx 在对称区间上是奇函数。
• 余弦函数 y = cosx 在对称区间上是偶函数。

常见三角函数图像展示如下：

• y = sinx 的图像是周期为 2π 的波形，经过原点 (0, 0)，最大值和最小值分别为 ±1。
• y = cosx 同样具有 2π 周期，图像经过点 (0, 1)，极值也为 ±1。

基本恒等式 —— 平方关系：
sinx + cosx = 1

在三角函数的恒等变换中，掌握基本公式是解决各类问题的关键。以下是对常用公式的整理与说明，内容包括二倍角、降幂、诱导、和角以及和差化积等相关公式，并对表达顺序进行了合理调整，以增强逻辑连贯性。

一、和角公式

和角与差角公式是三角恒等变形的基础，常用于展开或合并三角表达式：

sin(α + β) = sinα cosβ + cosα sinβ

sin(α β) = sinα cosβ cosα sinβ

cos(α + β) = cosα cosβ sinα sinβ

cos(α β) = cosα cosβ + sinα sinβ

二、二倍角公式

由和角公式可推导出二倍角形式，适用于角度加倍的情形：

sin2x = 2sinx cosx

cos2x = cosx sinx = 1 2sinx = 2cosx 1

三、降幂公式

将平方项转化为一次三角函数的形式，便于积分或化简：

sinx = (1 cos2x)/2

cosx = (1 + cos2x)/2

四、诱导公式

口诀：“奇变偶不变，符号看象限”。

对于 sin(kπ/2 + x) 的处理：

• 当 k 为偶数时，结果为 ±sinx；
• 当 k 为奇数时，结果为 ±cosx。

其中，正负号取决于将 x 视为锐角时，sin(kπ/2 + x) 所在象限的符号。

示例：

sin(π x) = sinx

sin(π + x) = sinx

sin(π/2 ± x) = cosx

对于 cos(kπ/2 + x) 的处理：

• 当 k 为偶数时，结果为 ±cosx；
• 当 k 为奇数时，结果为 ±sinx。

同样，± 号由 x 作为锐角时代入后，cos(kπ/2 + x) 的实际符号决定。

示例：

cos(π ± x) = cosx

cos(π/2 + x) = sinx

cos(π/2 x) = sinx

五、和差化积

将两个三角函数的和或差转化为乘积形式，有助于进一步简化运算（此处未列出具体公式，但其本质基于上述和角关系进行逆向推导）。

以下是三角函数中常见的和差化积与积化和差公式，以及正切、余切函数的基本性质整理。

一、和差化积公式

将两个三角函数的和或差转化为乘积形式，有助于简化运算：

• \(\sin\alpha + \sin\beta = 2\sin\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha - \beta}{2}\right)\)
• \(\sin\alpha - \sin\beta = 2\cos\left(\frac{\alpha + \beta}{2}\right)\sin\left(\frac{\alpha - \beta}{2}\right)\)
• \(\cos\alpha + \cos\beta = 2\cos\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha - \beta}{2}\right)\)
• \(\cos\alpha - \cos\beta = -2\sin\left(\frac{\alpha + \beta}{2}\right)\sin\left(\frac{\alpha - \beta}{2}\right)\)

二、积化和差公式

将两个三角函数的乘积转化为和或差的形式，常用于积分与恒等变换：

• \(\sin\alpha\cos\beta = \frac{1}{2}[\sin(\alpha + \beta) + \sin(\alpha - \beta)]\)
• \(\cos\alpha\sin\beta = \frac{1}{2}[\sin(\alpha + \beta) - \sin(\alpha - \beta)]\)
• \(\cos\alpha\cos\beta = \frac{1}{2}[\cos(\alpha + \beta) + \cos(\alpha - \beta)]\)
• \(\sin\alpha\sin\beta = -\frac{1}{2}[\cos(\alpha + \beta) - \cos(\alpha - \beta)]\)

三、正切函数与余切函数的基本性质

1. 一般表达式：

\(y = \tan x\)，\(y = \cot x\)

2. 定义域：

• 对于 \(y = \tan x\)，定义域为：\(x \neq k\pi + \frac{\pi}{2},\ k \in \mathbb{Z}\)
• 对于 \(y = \cot x\)，定义域为：\(x \neq k\pi,\ k \in \mathbb{Z}\)

3. 值域：

两者值域均为 \((-\infty, +\infty)\)。

4. 奇偶性：

在各自对称的定义区间内，\(y = \tan x\) 与 \(y = \cot x\) 均为奇函数。

5. 图像特征：

正切函数图像具有周期性，周期为 \(\pi\)，以直线 \(x = k\pi + \frac{\pi}{2}\) 为垂直渐近线，并经过原点。

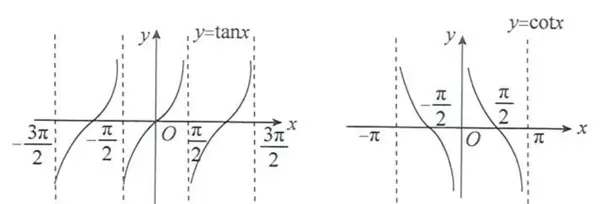
函数 y = cot x 的图像具有周期性，其基本周期为 π。该函数以直线 x = kπ（k 为整数）作为垂直渐近线，在每个区间 (kπ, (k+1)π) 内连续且单调递减。由于余切函数是正切函数的倒数，因此在正切为零的位置出现无穷间断点。

在三角恒等变换中，常用的平方关系式包括：

tanx + 1 = secx，以及 cotx + 1 = cscx

这两个公式分别由正弦与余弦的基本恒等式推导而来，广泛应用于积分、微分及表达式化简过程中。

关于倍角的运算，存在如下恒等式：

tan(2x) = (2 tan x) / (1 - tanx)，

cot(2x) = (cotx - 1) / (2 cot x)

这些公式可用于将双倍角度的三角函数表示为单角函数的形式，便于计算和分析。

对于两个角度之和或差的正切，适用以下和角公式：

tan(α ± β) = (tan α ± tan β) / (1 tan α tan β)

这一公式在解决复合角问题时非常关键，尤其在物理和工程中的波动分析中有广泛应用。

反三角函数部分

反三角函数是对基本三角函数进行反函数定义的结果，主要用于求解已知比值对应的角度。

1. 反正弦与反余弦函数

它们的一般形式为：y = arcsin x 和 y = arccos x。

这两个函数的定义域均为闭区间 [-1, 1]，而值域有所不同：

• arcsin x 的值域为 [-π/2, π/2]
• arccos x 的值域为 [0, π]

从对称性来看，y = arcsin x 是一个奇函数，即满足 arcsin(-x) = -arcsin(x)，在整个定义域内呈现中心对称特性。

此外，arcsin x 与 arccos x 均为有界函数，其输出值不会超出各自指定的范围。

一个重要且常用的关系式为：

arcsin x + arccos x = π/2

这表明对于任意 x ∈ [-1, 1]，反正弦与反余弦的和恒等于 π/2。

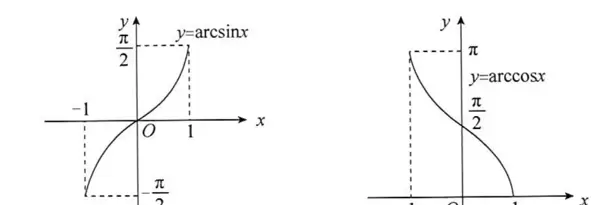
图像特征方面：

y = arcsin x 的曲线经过原点，定义域为 [-1, 1]，值域为 [-π/2, π/2]，整体呈单调上升趋势。

y = arccos x 则从点 (-1, π) 下降到 (1, 0)，同样定义在 [-1, 1] 上，值域为 [0, π]，单调递减。

2. 反正切与反余切函数

其标准表达式为：y = arctan x 与 y = arccot x。

这两者的定义域均为全体实数，即 (-∞, +∞)。

对应的值域分别为：

• arctan x ∈ (-π/2, π/2)
• arccot x ∈ (0, π)

其中，y = arctan x 是定义域内的奇函数，满足 arctan(-x) = -arctan(x)，图像关于原点对称。

两个函数都具有有界性，尽管输入可以趋向无穷大，但输出始终被限制在有限区间内。

一个重要的恒等关系为：

arctan x + arccot x = π/2

此式说明，对于任意实数 x，反正切与反余切的函数值之和恒为 π/2。

常见三角函数值表格：

x	0	π/6	π/4	π/3	π/2
sin x	0	1/2	√2/2	√3/2	1
cos x	1	√3/2	√2/2	1/2	0
tan x	0	√3/3	1	√3	不存在

指数函数的基本形式为：y = a^x，其中 a > 0 且 a ≠ 1。

定义域与值域：
定义域为 (∞, +∞)，值域为 (0, +∞)。

单调性特征：
当 a > 1 时，函数 y = a^x 单调递增；
当 0 < a < 1 时，函数 y = a^x 单调递减。

常见函数图像：

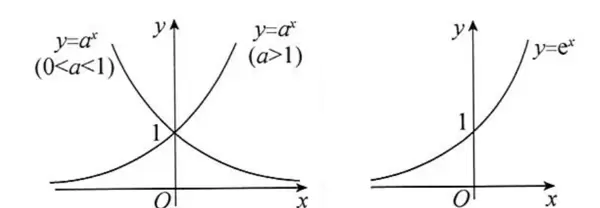
• y = a^x（0 < a < 1）：图像位于第一象限，随着 x 的增大而逐渐减小。
• y = a^x（a > 1）：图像位于第一象限，随 x 增大而上升。
• y = e^x：自然指数函数，图像在第一象限，x 增大时增长迅速。

极限行为：
当 x → +∞ 时，lim_x→+∞ e^x = +∞；
当 x → ∞ 时，lim_x→∞ e^x = 0。

特殊函数值：
a = 1，e = 1。

反三角函数的重要恒等式：

arctan x ± arctan y = arctan((x ± y)/(1 xy))

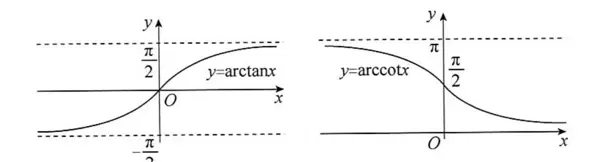
常见反三角函数图像及性质：
y = arctan x 的图像经过原点，定义域为 (∞, +∞)，值域为 (π/2, π/2)。
y = arccot x 的定义域为 (∞, +∞)，值域为 (0, π)。

极限特性：
lim_x→+∞ arctan x = π/2，
lim_x→∞ arctan x = π/2。