题目

给定一个二叉树的根节点，请你实现一个算法，用于计算该二叉树的垂序遍历序列。

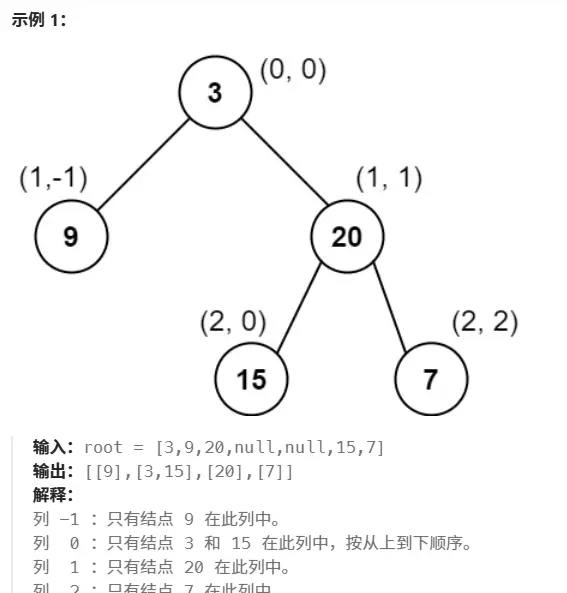
对于位于坐标 (row, col) 的任意节点，其左子节点位于 (row + 1, col - 1)，右子节点位于 (row + 1, col + 1)。根节点初始位置为 (0, 0)。

垂序遍历的规则如下：

• 从最左侧的列开始，依次处理每一列，直到最右侧的列；
• 每一列中的节点按照所在行的位置从上到下排列；
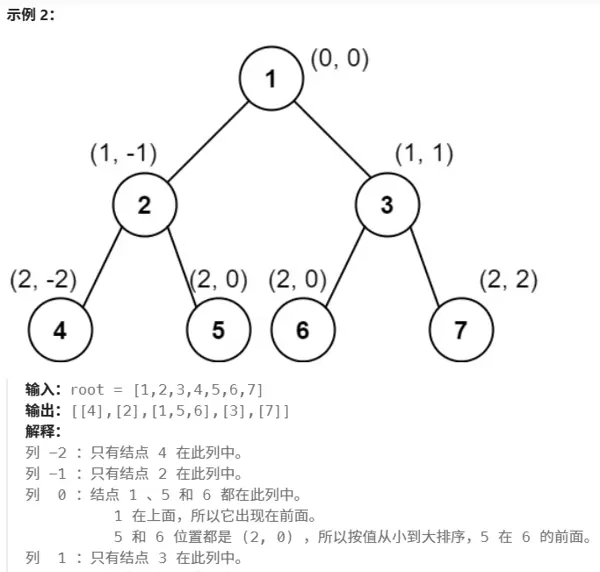
• 若多个节点处于同一行且同一列，则按节点值的大小升序排列；
• 最终返回每列中节点值的列表集合。

root

(row, col)

(row + 1, col - 1)

(row + 1, col + 1)

(0, 0)

解析

如何通过递归实现？

采用深度优先搜索（DFS）策略，遍历每一个节点，并在递归过程中传递当前节点的行号和列号：

• 左子树的行号为父节点行号加1，列号减1；
• 右子树的行号为父节点行号加1，列号加1。

使用一个哈希表（Map）来存储遍历过程中的节点信息：键为列号，值为该列中所有节点对应的 [行号, 节点值] 对组成的列表。

在完成整棵树的遍历后，对哈希表进行处理：

• 按照列号从小到大排序；
• 对每个列内的 [行号, 节点值] 列表进行排序：优先按行号升序，行号相同时按节点值升序；
• 提取排序后的节点值，组成新的列表，并加入结果集中。

最终返回结果集，即为所求的垂序遍历序列。

答案

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var verticalTraversal = function(root) {
    let res = [];
    const map = new Map();
    function dfs(node, row, col) {
        if(node === null) return;
        let list = map.get(col) || [];
        list.push([row, node.val]);
        map.set(col, list);
        dfs(node.left, row + 1, col - 1);
        dfs(node.right, row + 1, col + 1);
    }
    dfs(root, 0, 0);
    const cols = Array.from(map.keys()).sort((a, b) => a - b);
    for (const col of cols) {
        const nodes = map.get(col);
        nodes.sort((a, b) => a[0] - b[0] || a[1] - b[1]); 
        // 先按行号，行号相同按值
        const values = nodes.map(node => node[1]);
        res.push(values);
    }
    return res;
};

复杂度分析

• 时间复杂度：O(n log n)，其中 n 是二叉树的节点数量。主要开销来源于对各列中节点的排序操作；
• 空间复杂度：O(n)，用于存储所有节点的信息以及递归调用栈的空间消耗。