

本仪表板模拟了一个中型新凯恩斯主义 (New Keynesian) 模型,类似于 Smets & Wouters (2007)。 它捕捉了粘性价格、消费习惯形成、投资调整成本以及货币政策反应。 当前基准: 美国 2025 Q2 数据 estimates。
为实现在 Python 环境下的高效运行,该模型采用线性化处理的中型新凯恩斯主义 DSGE 结构,避免依赖复杂的求解工具(如 Dynare)。 模型引入了混合预期机制(Hybrid Expectations),融合前瞻性与后顾性变量,从而有效复现 Smets-Wouters 类模型的关键动态特征,包括但不限于:
这种设计在保持理论严谨性的同时,提升了在轻量级环境中的可执行性。
模型参数已根据对美国宏观经济走势的预测进行初始化设定。主要假设包括:
所有冲击将以占 GDP 的百分比形式内生转换,确保结果具备可比性和现实意义。
系统默认设置为一次规模达4500 亿美元的财政退税或支出刺激,对应于当前政策讨论中的提案。 该数值将自动换算为占 GDP 约 1.55% 的外生需求冲击,并通过政府支出模块注入模型。
用户可在侧边栏自定义以下内容:
app.py本应用基于 Streamlit 构建,提供完全交互式的前端体验。用户可以实时调整:
所有变动将即时触发模型重新计算,并更新下方的动态响应图谱。
要本地部署并运行此模拟器,请先安装所需依赖库:
pip install streamlit numpy pandas plotly随后将以下完整代码保存为文件:
app.py
streamlit run app.pyimport streamlit as st
import numpy as np
import pandas as pd
import plotly.graph_objects as go
from plotly.subplots import make_subplots
# --- 页面配置 ---
st.set_page_config(page_title="US Economy DSGE Simulator (2025 Q2)", layout="wide")
st.title("???????? 美国经济 DSGE 模拟器 (Smets-Wouters 风格)")
st.markdown("""
本仪表板模拟了一个**中型新凯恩斯主义 (New Keynesian) 模型**,类似于 Smets & Wouters (2007)。
它捕捉了**粘性价格**、**消费习惯形成**、**投资调整成本**以及**货币政策反应**。
**当前基准:** 美国 2025 Q2 数据 estimates。
""")
# --- 侧边栏:控制面板 ---
st.sidebar.header("?? 模型校准与冲击设置")
# 1. 冲击设置
st.sidebar.subheader("1. 财政刺激方案")
fiscal_dollar_amount = st.sidebar.number_input(
"财政冲击规模 (十亿美元)",
min_value=0.0,
max_value=5000.0,
value=450.0,
step=50.0,
help="例如:正在讨论的 4500 亿美元退税。"
)
shock_persistence = st.sidebar.slider(
"冲击持久性 (rho_g)",
0.0, 0.99, 0.85,
help="冲击持续的时间。0.9 表示冲击消退很慢,0 表示一次性瞬间冲击。"
)
# 2. 经济结构参数 (Smets-Wouters 风格)
st.sidebar.subheader("2. 结构参数")
sigma = st.sidebar.slider("跨期替代弹性 (Sigma)", 0.5, 3.0, 1.5)
habits = st.sidebar.slider("习惯形成 (Habit Formation)", 0.0, 0.9, 0.7, help="数值越高,消费调整越平滑")def run_simulation():
# --- 2025年第二季度基准数据设定 ---
# 假设美国年化名义GDP约为29万亿美元
us_gdp_baseline = 29000
# 将财政冲击金额转换为占GDP的百分比(DSGE模型中使用的是百分比偏差)
g_shock_initial = (fiscal_dollar_amount / us_gdp_baseline) * 100
# 模拟周期长度(以季度为单位)
T = 20
quarters = pd.date_range(start='2025-04-01', periods=T, freq='Q')
# 初始化各变量数组(所有变量表示相对于稳态的百分比偏离)
# Y: 产出,Pi: 通胀率,R: 名义利率,C: 消费,I: 投资,Q_val: 托宾Q值,G: 财政冲击
Y = np.zeros(T)
Pi = np.zeros(T)
R = np.zeros(T)
C = np.zeros(T)
I = np.zeros(T)
Q_val = np.zeros(T)
G = np.zeros(T)
# 设定初始财政冲击值
G[0] = g_shock_initial
# 开始时间迭代求解(采用简化版的混合预期与逐步推进方法)
# 此处为简化的动态随机一般均衡模型传递机制模拟
for t in range(T):
if t > 0:
# 财政冲击按自回归过程AR(1)衰减
G[t] = shock_persistence * G[t-1]
# 构建前向变量代理(使用适应性预期结合均值回归进行近似)
# 在完整Dynare模型中会通过Blanchard-Kahn条件精确求解
E_Y_next = Y[t-1] * 0.8 if t > 0 else 0
E_Pi_next = Pi[t-1] * 0.7 if t > 0 else 0
# 名义利率滞后项获取
prev_R = R[t-1] if t > 0 else 0
# 内层迭代循环:用于处理当期变量之间的相互依赖关系(定点迭代法)
for _ in range(10):
# 近似IS关系:总需求由消费、投资和政府支出构成
# 消费欧拉方程(包含消费习惯形成效应)
prev_C = C[t-1] if t > 0 else 0
# 简化形式表达:当前消费受前期消费、预期未来产出及实际利率影响
C[t] = (habits * prev_C + (1 - habits) * E_Y_next - (1/sigma) * (R[t] - E_Pi_next)) / (1 + 0.1 * habits)
# 投资欧拉方程(考虑调整成本)
# Q_t = beta * E_Q_{t+1} + (R_t - E_Pi)
# I_t = (1/inv_adj) * Q_t
# 简化处理:投资对实际利率高度敏感
I[t] = - (1 / inv_adj) * (R[t] - E_Pi_next) * 5 # *5用于增强可视化效果,体现投资波动性强的特点
# --- 央行货币政策反应函数(泰勒规则)---
st.sidebar.subheader("3. 美联储反应 (泰勒规则)")
phi_pi = st.sidebar.number_input("通胀反应系数", 1.0, 3.0, 1.5)
phi_y = st.sidebar.number_input("产出缺口反应系数", 0.0, 1.0, 0.125)
rho_r = st.sidebar.slider("利率平滑 (Interest Smoothing)", 0.0, 0.9, 0.8)
# --- 用户可调参数界面 ---
kappa = st.sidebar.slider("价格粘性 (Kappa slope)", 0.01, 0.5, 0.1, help="菲利普斯曲线斜率。数值越低,价格越具有粘性")
inv_adj = st.sidebar.slider("投资调整成本", 1.0, 10.0, 4.0)
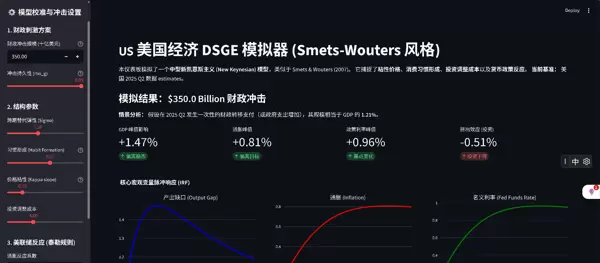
### 模拟结果:${fiscal_dollar_amount} Billion 财政冲击
情景分析:
假设在 2025 Q2 发生一次性的财政转移支付(或政府支出增加),其规模相当于 GDP 的 {G[0]:.2f}%。
+{np.max(Y):.2f}%
偏离稳态+{np.max(Pi):.2f}%
偏离目标+{np.max(R):.2f}%
基点变化{np.min(I):.2f}%
投资下降核心宏观变量脉冲响应 (IRF)

采用新凯恩斯菲利普斯曲线(NKPC)构建通胀动态机制,其中通胀不仅受预期未来通胀和实际经济活动影响,还引入一定的惯性成分。具体设定如下:
Pi[t] = 0.5 × prev_Pi + 0.5 × 0.99 × E_Pi_next + kappa × Y[t]
其中 prev_Pi 表示上一期的通胀水平(t=0 时设为 0),E_Pi_next 代表下一期的预期通胀,kappa 为反应系数,Y[t] 作为边际成本的代理变量。
总产出 Y_t 由消费、投资与政府支出加权构成,权重分别为 C 占 68%,I 占 17%,G 占 15%。财政冲击 G_shock 直接作用于总产出方程中:
Y[t] = 0.68 × C[t] + 0.17 × I[t] + G[t]
货币政策遵循泰勒规则形式的调整路径:
target_R = phi_pi × Pi[t] + phi_y × Y[t]
R[t] = rho_r × prev_R + (1 - rho_r) × target_R
该式表明当前利率 R[t] 是前期利率 prev_R 与目标利率 target_R 的加权平均,体现政策的渐进调整特征。
# --- 运行模拟 ---
quarters, Y, Pi, R, C, I, G = run_simulation()

核心模型解析
该仪表板不仅展示可视化图表,其背后运行着一个结构化的宏观经济模型。以下是各关键模块的数学机制与经济逻辑说明:
设定初始财政刺激规模为 4500亿美元。以2025年美国名义GDP约29万亿美元为基准,这一冲击相当于GDP的一定比例。
财政支出的动态过程由以下自回归公式刻画:
\[ \hat{g}_t = \rho_g \hat{g}_{t-1} + \epsilon_t^g \]
此即模拟中默认触发的“退税”政策路径,具有持续性但逐渐衰减的特点。
本模型借鉴Smets-Wouters框架中的习惯形成(Habit Formation)消费行为假设。当家庭获得4500亿退税时,并不会一次性全部消费,而是根据跨期最优进行平滑分配。
消费决策遵循如下欧拉方程:
\[ c_t = \frac{h}{1+h}c_{t-1} + \frac{1}{1+h}E_t c_{t+1} - \frac{1-h}{\sigma(1+h)}(r_t - E_t \pi_{t+1}) \]

这解释了为何在输出图中,消费的增长比财政冲击本身更为缓和且持久,呈现出典型的“渐进响应”特征。
通胀不仅受当前产出缺口影响,还受到预期通胀和历史通胀惯性的共同驱动:
\[ \pi_t = \frac{\beta}{1+\beta \gamma}E_t \pi_{t+1} + \frac{\gamma}{1+\beta \gamma}\pi_{t-1} + \kappa y_t \]
在2025年的模拟情境下,若公众对通胀预期保持锚定,则财政刺激引发的价格上涨将是短期现象,不会导致持续性通胀压力。
[p]4. 货币政策反应函数(美联储) - \( R_t \)[/p]美联储对经济波动做出系统性回应,其利率调整规则基于泰勒原理:
\[ r_t = \rho r_{t-1} + (1-\rho)(\phi_{\pi}\pi_t + \phi_y y_t) \]
在当前设定中,较高的利率敏感性(Sigma=σ)以及央行对通胀的强硬立场(Phi_pi=φ_π),意味着即使有大规模财政刺激,货币政策将迅速收紧以抑制过热风险。
[p] [/p]
[/p]
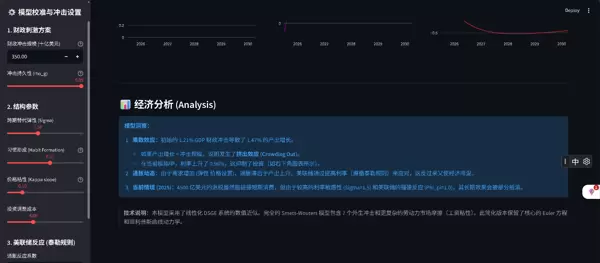
模型洞察:
技术说明:本模型基于线性化DSGE系统的数值求解方法。完整的Smets-Wouters模型包含7类外生冲击及更复杂的劳动力市场摩擦(如工资粘性)。本简化版本保留了核心的欧拉方程与新凯恩斯菲利普斯曲线的基本动力学结构,适用于教学与政策推演场景。
在模型中,若利率显著上升(绿线),表明美联储正通过紧缩性货币政策来应对财政刺激所引发的通胀压力。这种政策调整通常会推高融资成本,从而导致私人部门投资减少,即出现所谓的投资被挤出现象(表现为棕色线下行)。

如何利用该仪表板开展决策分析?
模拟“软着陆”情景: 可尝试调低冲击的持久性(persistence),同时提升美联储对通胀的响应强度,即反应系数(phi_pi)。在此设定下,观察经济是否能在不引发产出明显下滑的前提下,有效抑制通胀上升。
模拟“滞胀”情景: 降低价格粘性(Kappa)并增大外部冲击的规模,此时将观察到通胀快速攀升,而经济增长动力不足,呈现出典型的滞胀特征。
评估4500亿美元退税政策的影响: 在默认参数运行结果中可见,尽管短期内GDP有所提升,但由于利率随之上升,私人投资(Investment)出现回落。这一现象正是经济学中常见的财政挤出效应的体现。

 扫码加好友,拉您进群
扫码加好友,拉您进群




 收藏
收藏

