一、图神经网络在传感器网络中的核心思想

将传感器网络类比为一个“社交网络”，是理解图神经网络（GNN）应用的关键视角。

设想一个由温度、湿度和气压等多种传感器构成的监测系统：

传统方式处理模式

每个传感器被视为彼此独立的数据源，单独进行数据分析。例如：“传感器A显示25°C，传感器B记录到26°C”……这种做法忽略了它们之间可能存在的物理联系与相互影响。

GNN的全新视角：构建传感器“社交圈”

• 每个人 = 一个传感器节点
• 朋友关系 = 传感器之间的空间关联（如距离远近、风向传播路径或物理连接）
• 聊天内容 = 各传感器采集的数据（如温度、湿度等）
• 影响力传播 = 某个传感器出现异常时，其“邻居”也会受到波及

技术本质解析

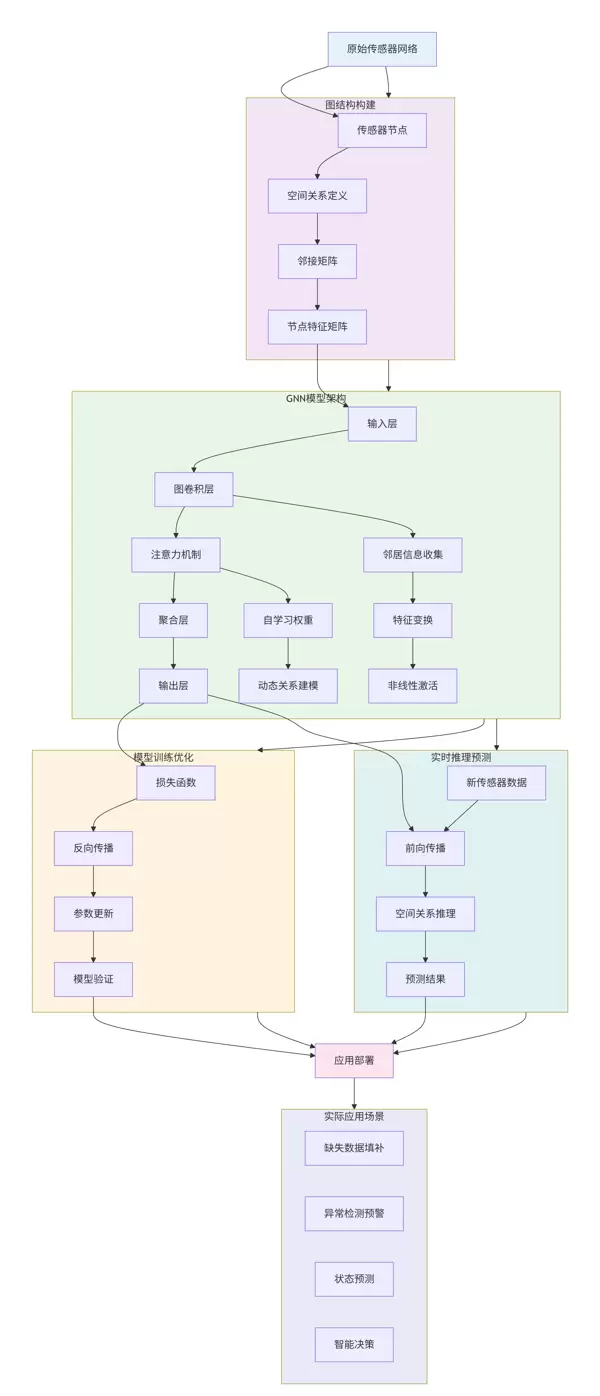
图神经网络的核心在于：将现实世界中分布式的传感器网络抽象成图结构（Graph），并通过节点间的信息传递机制，学习每个传感器在其局部空间环境下的增强特征表示。

三大构成要素：

1. 节点：代表单个传感器，携带自身的观测数据作为特征输入。
2. 边：反映传感器之间的空间关系，包括地理距离、连通性以及物理约束条件。
3. 信息传递：通过邻接节点间的交互，实现特征聚合与上下文感知。

二、为何选择GNN来建模传感器空间关系？

传统方法面临的挑战

1. 独立性假设缺陷

忽视了传感器之间的空间相关性。例如，上游某点发生污染，下游区域很快会受到影响，但传统模型无法自动捕捉此类动态传播过程。

# 传统机器学习方法
for sensor in sensors:
    predict(sensor.data)  # 每个传感器独立预测

2. 手工特征工程复杂且低效

• 需人为定义哪些传感器属于“相邻”范围
• 必须手动构造“空间权重矩阵”
• 难以表达非线性、复杂的依赖关系

3. 难以应对动态变化

• 传感器网络可能随时间调整（新增、移除或故障）
• 空间影响关系并非固定不变（如风向改变导致扩散路径变化）

GNN带来的突破性优势

自动学习空间依赖关系

无需人工设定权重，GNN能够从数据中自主推断出传感器之间的相互影响强度。

支持不规则拓扑结构

现实中传感器往往呈非均匀分布，而非理想化的网格布局。GNN天然适用于任意图结构，灵活适应各种部署场景。

强大的泛化能力

训练完成的模型可迁移至不同规模或布局的新网络，并能快速接纳新加入的传感器节点。

实现端到端的学习流程

直接从原始传感数据映射到最终预测结果，减少中间环节造成的信息损失。

三、具体实施步骤详解

步骤1：构建传感器图结构

首先需要明确两个关键部分：

• 节点特征定义：将每个传感器的实时读数（如温度、湿度）作为节点属性。
• 邻接矩阵设计：基于空间距离、方向性因素或其他物理规律建立边连接关系。

import torch
import numpy as np

# 假设有5个温度传感器
num_sensors = 5

# 节点特征矩阵：每个传感器的历史数据
# 形状：[节点数, 特征维度]
node_features = torch.tensor([
    [25.0, 65, 1013],  # 传感器0: [温度, 湿度, 气压]
    [26.0, 62, 1012],  # 传感器1
    [24.5, 68, 1014],  # 传感器2
    [25.8, 63, 1013],  # 传感器3
    [23.9, 70, 1015]   # 传感器4
], dtype=torch.float)

print(f"节点特征形状: {node_features.shape}")  # [5, 3]

# 基于距离的空间关系
# 假设传感器间的距离矩阵
distance_matrix = torch.tensor([
    [0, 1.0, 2.5, 1.8, 3.2],  # 传感器0到其他传感器的距离
    [1.0, 0, 1.8, 0.9, 2.5],
    [2.5, 1.8, 0, 2.0, 1.2],
    [1.8, 0.9, 2.0, 0, 1.8],
    [3.2, 2.5, 1.2, 1.8, 0]
])

# 将距离转换为连接关系（距离越小，连接越强）
threshold = 2.0  # 距离阈值
adjacency_matrix = (distance_matrix > 0) & (distance_matrix <= threshold)
adjacency_matrix = adjacency_matrix.float()

print("邻接矩阵:")
print(adjacency_matrix)
# 输出：
# tensor([[0., 1., 0., 1., 0.],
#         [1., 0., 1., 1., 0.],
#         [0., 1., 0., 0., 1.],
#         [1., 1., 0., 0., 1.],
#         [0., 0., 1., 1., 0.]])

步骤2：设计合适的GNN模型架构

根据任务需求选择图卷积网络（GCN）、图注意力网络（GAT）或其他变体，确保模型具备足够的表达能力和可解释性。

import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
import torch_geometric

class SensorGNN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(SensorGNN, self).__init__()
        # 图卷积层
        self.conv1 = GCNConv(input_dim, hidden_dim)
        self.conv2 = GCNConv(hidden_dim, hidden_dim)
        # 预测层
        self.predictor = nn.Linear(hidden_dim, output_dim)
        
    def forward(self, x, edge_index):
        # x: 节点特征 [num_nodes, input_dim]
        # edge_index: 边索引 [2, num_edges]
        
        # 第一层图卷积 + 激活函数
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        
        # 第二层图卷积
        x = self.conv2(x, edge_index)
        x = F.relu(x)
        
        # 最终预测
        output = self.predictor(x)
        return output

# 将邻接矩阵转换为边索引（GNN需要的格式）
edge_index = torch_geometric.utils.dense_to_sparse(adjacency_matrix)[0]

print(f"边索引形状: {edge_index.shape}")  # [2, num_edges]

步骤3：完整的训练与推理流程

包含数据预处理、图构建、前向传播、损失计算与参数优化等阶段，形成闭环学习体系。

class SensorNetworkGNN:
    def __init__(self, num_sensors, feature_dim):
        self.num_sensors = num_sensors
        self.model = SensorGNN(
            input_dim=feature_dim, 
            hidden_dim=64, 
            output_dim=1  # 预测温度
        )
        self.optimizer = torch.optim.Adam(self.model.parameters(), lr=0.01)
        self.loss_fn = nn.MSELoss()
        
    def prepare_graph_data(self, sensor_data, distance_matrix):
        """准备图数据"""
        # 节点特征：传感器数据
        node_features = torch.tensor(sensor_data, dtype=torch.float)
        
        # 构建邻接矩阵（基于距离）
        adjacency_matrix = (distance_matrix > 0) & (distance_matrix <= 2.0)
        adjacency_matrix = adjacency_matrix.float()
        
        # 转换为边索引
        edge_index = torch_geometric.utils.dense_to_sparse(adjacency_matrix)[0]
        
        return node_features, edge_index, adjacency_matrix
    
    def train(self, train_data, distance_matrix, epochs=100):
        """训练模型"""
        node_features, edge_index, _ = self.prepare_graph_data(
            train_data, distance_matrix
        )
        
        self.model.train()
        for epoch in range(epochs):
            self.optimizer.zero_grad()
            
            # 前向传播
            predictions = self.model(node_features, edge_index)
            
            # 计算损失 - 假设预测下一个时间步的温度
            targets = torch.tensor(train_data[:, 0] + 0.1, dtype=torch.float).unsqueeze(1)
            loss = self.loss_fn(predictions, targets)
            
            # 反向传播
            loss.backward()
            self.optimizer.step()
            
            if epoch % 20 == 0:
                print(f'Epoch {epoch}, Loss: {loss.item():.4f}')
    
    def predict(self, new_sensor_data, distance_matrix):
        """使用训练好的模型进行预测"""
        self.model.eval()
        with torch.no_grad():
            node_features, edge_index, _ = self.prepare_graph_data(
                new_sensor_data, distance_matrix
            )
            predictions = self.model(node_features, edge_index)
            return predictions.numpy()

# 使用示例
if __name__ == "__main__":
    # 模拟传感器数据 [温度, 湿度, 气压]
    sensor_data = np.random.rand(5, 3) * 10 + 20  # 5个传感器，3个特征
    
    # 模拟距离矩阵
    dist_matrix = torch.tensor([
        [0, 1.2, 2.1, 1.8, 2.9],
        [1.2, 0, 1.5, 0.8, 2.3],
        [2.1, 1.5, 0, 1.9, 1.1],
        [1.8, 0.8, 1.9, 0, 1.7],
        [2.9, 2.3, 1.1, 1.7, 0]
    ])
    
    # 创建并训练GNN模型
    gnn_model = SensorNetworkGNN(num_sensors=5, feature_dim=3)
    gnn_model.train(sensor_data, dist_matrix)
    
    # 进行预测
    new_data = sensor_data + np.random.normal(0, 0.1, sensor_data.shape)
    predictions = gnn_model.predict(new_data, dist_matrix)
    print("预测结果:", predictions.flatten())

步骤4：引入高级技巧——动态空间关系建模

使用动态图机制（如时间感知注意力）让模型能适应随时间演变的空间依赖结构，提升对突发情况的响应能力。

# 对于动态变化的空间关系，可以使用注意力机制
class AttentionSensorGNN(nn.Module):
    def __init__(self, input_dim, hidden_dim):
        super(AttentionSensorGNN, self).__init__()
        # 使用图注意力层
        self.attention_conv = GATConv(input_dim, hidden_dim, heads=1)
        
    def forward(self, x, edge_index):
        # 自动学习传感器间的重要性权重
        x = self.attention_conv(x, edge_index)
        return x

# 这样模型可以自动学习：
# - 在刮风天，上风向的传感器更重要
# - 在炎热天，阴凉处的传感器更可靠

四、典型应用场景展示

1. 环境监测网络

• 填补缺失传感器数据
• 识别异常读数节点
• 模拟并预测污染物扩散路径

2. 工业设备状态监控

• 预警设备故障的连锁传播
• 优化现有传感器布设方案
• 融合多源传感信息提升判断精度

3. 智能交通系统

• 精准预测城市交通流量趋势
• 分析交通事故的影响范围
• 动态优化红绿灯控制策略

4. 智慧农业领域

• 预测农田微气候变化
• 制定高效灌溉计划
• 提前预警病虫害传播风险

总结：GNN如何重塑传感器网络能力

对比维度	传统方法	GNN方法
分析模式	传感器独立分析	网络协同分析
空间关系处理	人工定义	自动学习
适用结构	规则网格	任意拓扑
关系性质	静态不变	动态自适应

核心优势归纳：

• 空间感知能力：模型清楚知道“谁靠近谁”，具备地理上下文意识。
• 信息聚合机制：每个节点的输出都融合了周边邻居的信息，提升决策质量。
• 系统鲁棒性强：即使个别传感器失效，整体仍可通过邻域补偿维持功能。
• 具有一定可解释性：借助注意力权重等机制，可以可视化分析各传感器间的实际影响程度。

通过引入图神经网络，原本分散孤立的传感器群体被转化为一个具备协作智能的整体系统，显著增强了环境感知、异常检测与未来趋势预测的准确性与可靠性。