描述性分析用于描述定量数据的整体情况，例如研究消费者对于某商品的购买意愿情况，可用到描述性分析对样本的年龄、收入、消费水平等各指标进行初步分析，以了解掌握消费者总体的特征情况。

描述分析应用场景

通过描述性分析计算数据的集中性特征（平均值）和波动性特征(标准差值),以了解数据的基本情况。因此在研究中经常是首先进行描述性分析，再次基础之上再进行深入的分析。

描述性分析还可用于查看数据是否有异常情况（最小值或最大值查看），比如数据中出现-2，-3等异常情况。

常见的描述指标

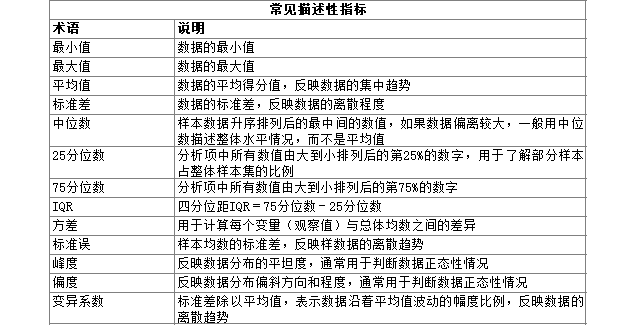
常见描述性指标说明

• 最大值、最小值可用来检验数据是否存在异常情况。
• 平均值、中位数是用于描述数据的集中趋势指标。
• 标准差是用于描述数据的离散趋势指标。如果比较单位不同（或数值相差太大）的两组数据时，采用变异系数比较离散程度。
• 峰度和偏度通常用于判断数据正态性情况，峰度的绝对值越大，说明数据越陡峭，峰度的绝对值大于3，意味着数据严重不正态。同时偏度的绝对值越大，说明数据偏斜程度越高，偏度的绝对值大于3，意味着严重不正态（可通过正态图查看数据正态性情况）。

案例应用

目标：对各类居民消费指数进行统计描述

Step1：将分析项拖拽至选框中，点击“开始描述分析”

描述性分析界面

Step2：生成分析结果

基础指标

深入指标

Step3：结果分析

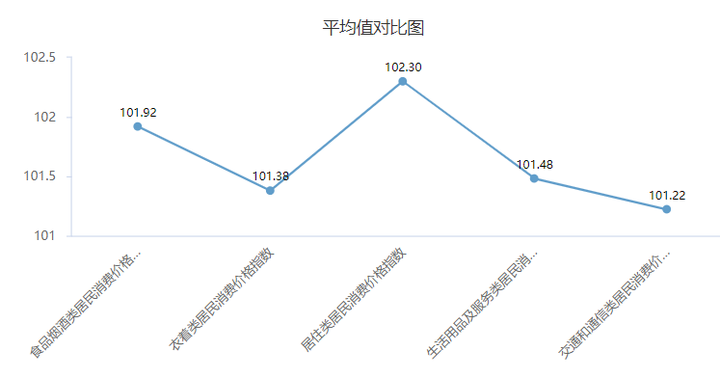
以‘食品烟酒类居民消费价格指数’为例（以下简称食品类消费指数），对上表数据进行分析可知：

1. 集中趋势指标：可见食品类消费指数均值为101.923，中位数为102.000，两者差异不大。
2. 离散趋势指标：食品类消费指数方差为0.832，最大值为103.500，最小值为100.700，，两者之差为全距2.8，说明数据较为稳定。
3. 参数估计：可见食品类消费指数均数的标准误为0.253，相应的总体均数95%置信区间为101.427~102.419
4. 分布特征指标：总指标峰度为-1.160，偏度为0.186。

其他说明

1、一般采用平均值加标准差来描述数据的整体情况。

2、当数据呈现严重偏态时，采用中位数描述数据的整体水平情况，而不是平均值。

3、除了使用描述性分析外，也建议使用箱线图直观展示数据分布情况。