一、应用
通俗地讲,熵权TOPSIS法是先使用熵权法得到新数据newdata(数据成熵权法计算得到的权重),然后利用新数据newdata进行TOPSIS法研究。
二、操作
SPSSAU操作
(1)点击SPSSAU综合评价里面的‘熵权TOPSIS’按钮。如下图
(2)拖拽数据后点击开始分析
三、数据处理
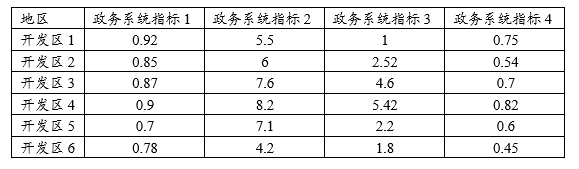
四、案例背景
当前有6个国家经济技术开发区,分别在政务系统的4个指标上的评分值。数字越大表示指标越优。当前希望利用熵权TOPSIS法评价出6个开发区的政务系统排名情况。本例子的数据已经全部是正向指标,因此不需要进行正向化或逆向化处理;如果说指标中有负向指标;则需要让数据全部‘正向化’,针对正向指标做正向处理,负向指标做逆向处理。原始数据如下:
五、分析结果
SPSSAU生成的分析结果如下
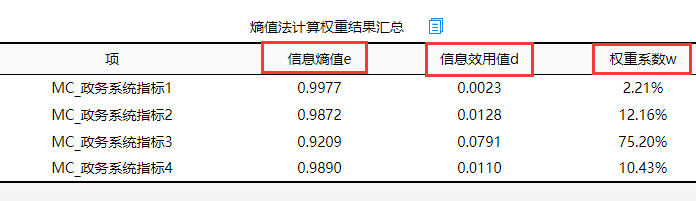
1.熵值法计算权重结果汇总
(1)信息熵值_e_
计算第j项指标下第i个样本值占比重
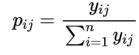
计算各指标的信息熵(列)
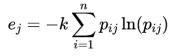
式中,k=1/ln(n);
(2)信息效用值d
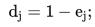
(3)权重系数
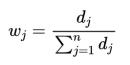
分析1
上表格展示出4个政务系统指标的权重值,明显可以看出指标3的权重更大。但权重大小仅仅是过程值,熵值TOPSIS分析重心在于TOPSIS法计算出相对接近度。权重值与数据相乘,得到新数据newdata,这一过程是SPSSAU自动完成,利用newdata进行TOPSIS法计算。
- TOPSIS评价计算结果
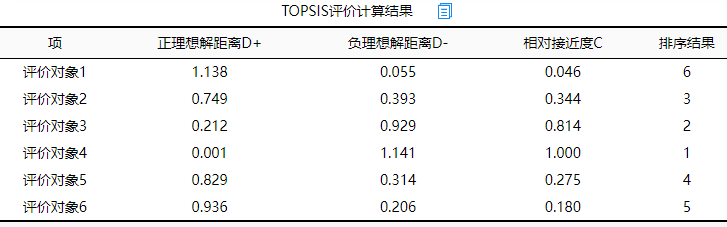
(1)正理想解距离D+
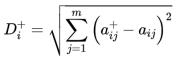
式中,最优方案 ![[公式]](https://www.zhihu.com/equation?tex=+%5Cmathbf%7BA%7D%5E%7B%2B%7D%3D%5Cleft%28a_%7Bi+1%7D%5E%7B%2B%7D%2C+a_%7Bi+2%7D%5E%7B%2B%7D%2C+%5Ccdots%2C+a_%7Bi+m%7D%5E%7B%2B%7D%5Cright%29%EF%BC%9Ba_%7Bi+j%7D) 为矩阵A中元素。
为矩阵A中元素。
(2)负理想解距离D-
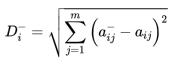
式中,最劣方案 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmathbf%7BA%7D%5E%7B-%7D%3D%5Cleft%28a_%7Bi+1%7D%5E%7B-%7D%2C+a_%7Bi+2%7D%5E%7B-%7D%2C+%5Ccdots%2C+a_%7Bi+m%7D%5E%7B-%7D%5Cright%29)
(3)相对接近度C
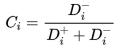
分析2
最终从上表可知:评价对象4,即开发区4,它的相对接近度C值最高,因而说明开发区4在政务系统上的表现最优;其次是开发区3,相对接近度C起来0.814。开发区1的政务系统表现最差。
- 正负理想解
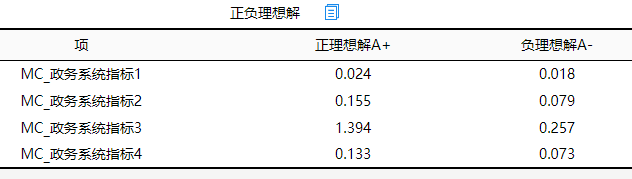
(1)正理想解A+
指标数据中最大值;例:MC_政务系统指标1为0.024;
(2)负理想解A-
指标数据中最大值;例:MC_政务系统指标1为 0.018;
分析3
正负理想解为计算正负理想距离值的过程值,一般不用过多关注。其代表某指标对应的最优或最劣值,在这里即为最大值或最小值。

 扫码加好友,拉您进群
扫码加好友,拉您进群