通过欧式距离计算出点与点的远近，圆点代表待分类的点，方点与三角点代表训练数据中已经分好成两类的数据。可以看出，在指定的半径1中，三角点个数比方点个数多一个，K最邻近算法会将圆点分成三角点一类，在指定半径2中，方点比三角点多一个，所以K最邻近算法会将圆点分成方点一类。

K最近邻算法的使用会存在一些假设。首先假设在相同类型中的客户拥有同样的行为，其次假设需要判别的点会做与其邻居相同的事情。如果这些假设条件不满足的话，KNN的效果也会大打折扣的。

另外把K最近邻算法归入到基本的数据挖掘技术，是因为KNN本身并不是一个可以自行学习的算法，它只是机械的计算与周围邻居的距离，所以这个算法本身的效率比较低。比如最开始的数据集有100万条，对于一条待分类的数据，KNN会计算所有100条数据的距离，在进行排序，取前k个邻居，再进行类别判断。对于下一条待分类的数据也是如此计算。我们在对实例实施K最近邻的算法之前，首先要注意，我们需要对数据的量纲进行处理。K最近邻算法主要计算实例间的距离远近，如果实例中的变量单位不同或者量纲差别很大，会影响到距离计算的结果。如下图所示，Income的单位是万，而Age的单位是十，如果在单位量纲不变的情况下直接计算距离，由于这两个属性的量纲差距很大，Age这个单位量纲较小的属性在距离计算中的权重太小，甚至被忽略，这个情况显然不是我们所期望的。

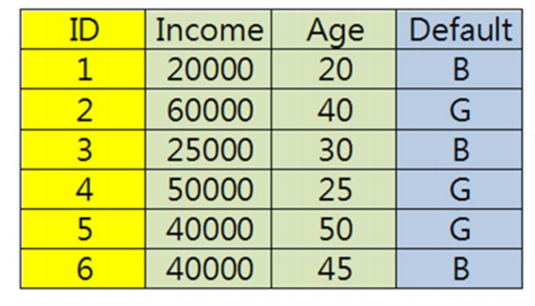
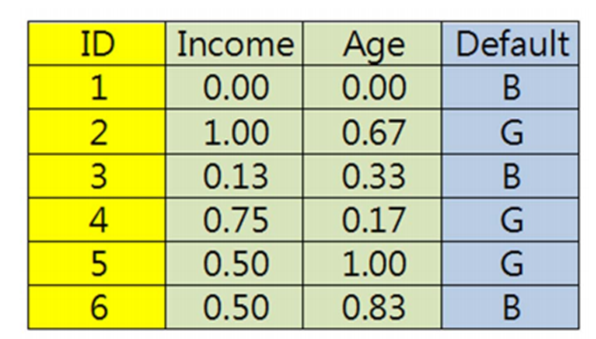
所以首先我们先要对变量中的属性进行极值正规化，进行计算的公式也很简单，就是（原始值-该属性中的最小值/属性中的最大值-最小值）如下图所示。

那我们举例来说，比如原数据中Income为25000，那极值正规化的结果为25000-20000/60000-20000=0.125，根据变量精度要求，四舍五入为0.13，如下图所示。Income以及其他需要极值正规化处理的属性中的其他值也如此带入公式，求出结果。