1深度学习概述

what深度学习

• 深度学习是一种机器学习方法，通过多层次的神经网络学习数据的表示和特征。它着重于使用具有多个层次的神经网络模型来学习复杂的表征，这些层次从原始数据中提取并组合出越来越抽象和高级的特征。
• 神经网络这一术语来自于神经生物学，虽然其一些核心概念是从人们对大脑的理解中汲取部分灵感而形成的，但深度学习模型不是大脑模型。 没有证据表明大脑的学习机制与现代深度学习模型所使用的相同 。
  

why深度学习

• 自动特征提取
  

：传统机器学习依赖于手工提取特征，而其能够自动学习数据的特征，省去了复杂的特征提取和选择过程。处理复杂数据：深度学习擅长处理非结构化数据

• ，如图像、视频和文本，可以从中提取复杂的模式和关系。
• 提高准确性：随着数据量的增加，深度学习模型的性能会持续提高。
  

how深度学习

深度学习的学习的三个层次

• what：深度学习有哪些技术，以及哪些技术可以帮你解决问题。
  
  • AI相关人员：掌握What，知道名词，能干什么。
    
• how：如何实现（产品 or paper）和调参（精度or速度）。
  
  • 数据科学家、工程师：掌握What、How，手要快，能出活。
    
• why：背后的原因（直觉，数学）。
  
  • 研究员、学生：掌握What、How、Why，除了知道有什么和怎么做，还要知道为什么，思考背后的原因，做出新的突破
    

深度学习的理解

经典程序设计和机器学习的区别

机器学习：一种新的编程范式

机器学习和深度学习的区别

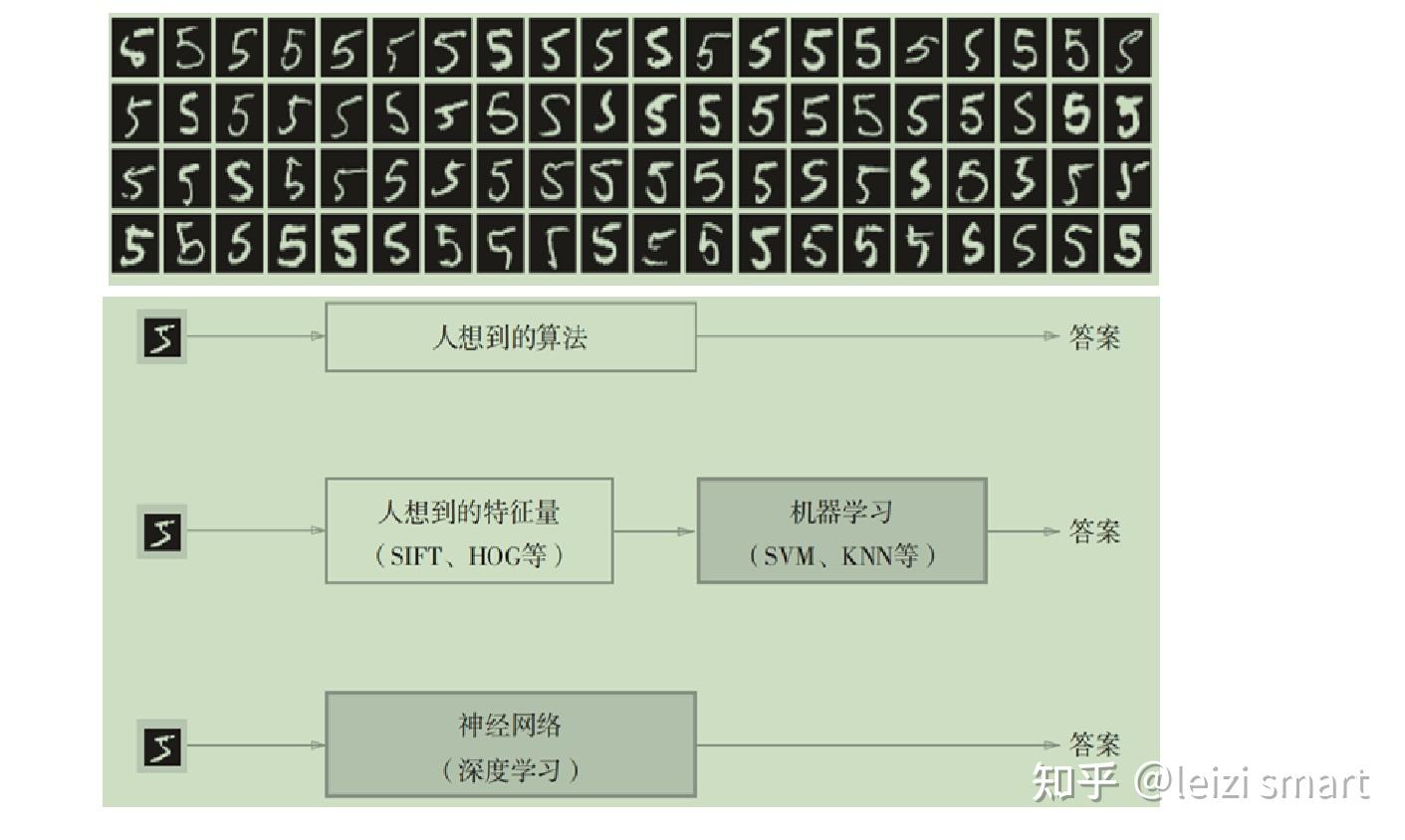
深度学习原理

• 权重：神经网络是由其权重来参数化（权重weight，其本质是一串数字）。开始权重随机赋值，因此网络只是实现了一系列随机变换。其输出结果自然也和理想值相去甚远，相应地，损失值也很高。
• 损失函数：用来衡量该输出与预期值之间的距离。具有最小损失值的神经网络，其输出值与目标值尽可能地接近，这就是一个训练好的神经网络
• 优化器：深度学习是利用这个距离值作为反馈信号来对权重值进行微调，以降低当前示例对应的损失值。 这种调节由优化器（optimizer）来完成，它实现了所谓的反向传播（backpropagation）算法。
• 随着网络处理的示例越来越多，权重值也在向正确的方向逐步微调，损失值也逐渐降低。这就是训练循环（training loop），将这种循环重复足够多的次数（通常对数千个示例进行数十次迭代），得到的权重值可以使损失函数最小。具有最小损失的网络，其输出值与目标值尽可能地接近，这就是训练好的网络。
• 通常模型的收敛条件可以有以下3个：（1）loss小于某个预先设定的较小的值；（2）两次迭代之间权值的变化已经很小了；（3）设定最大迭代次数，当迭代次数超过最大迭代次数时停止
  

网络、层、损失函数和优化器之间的关系

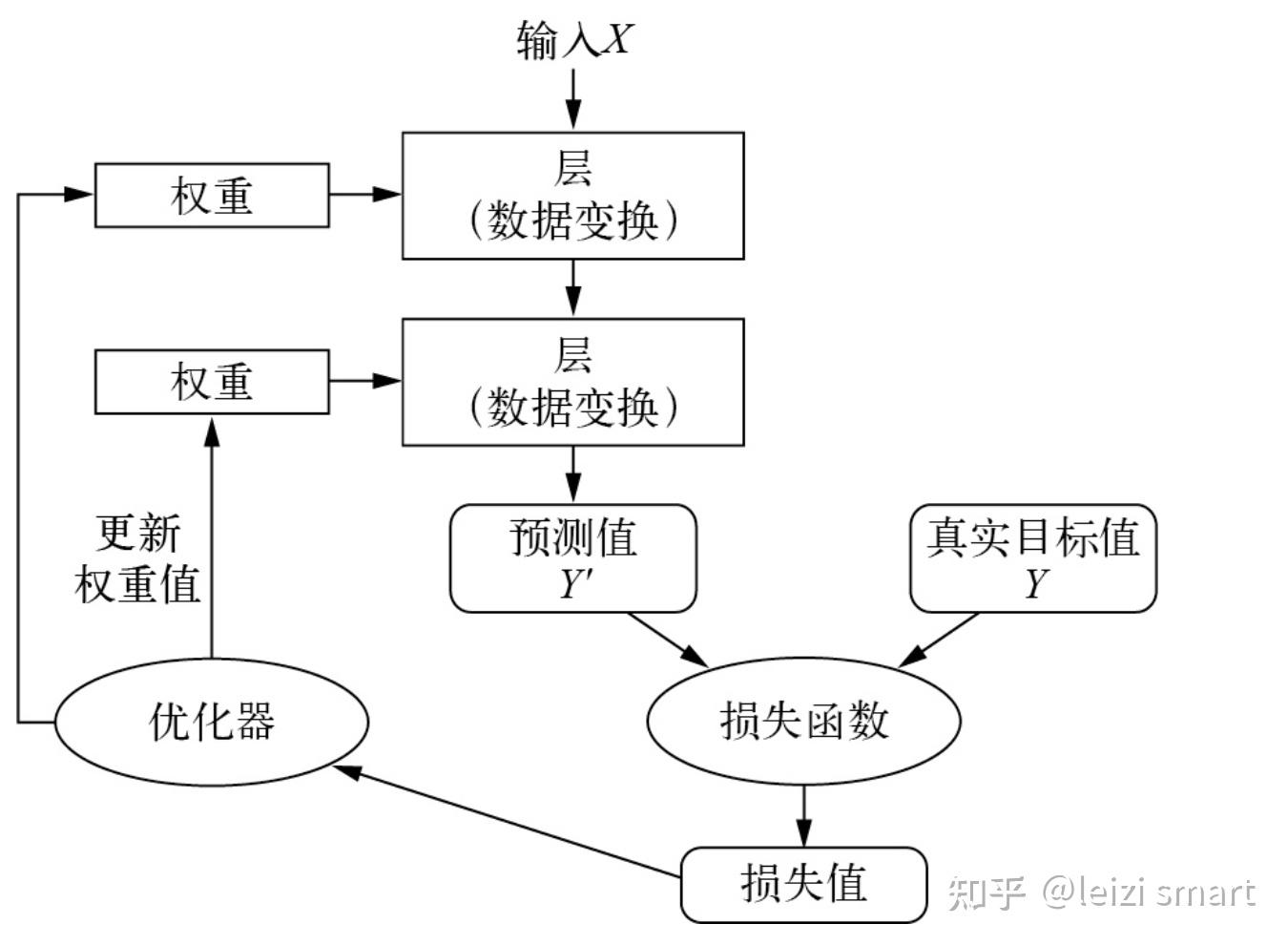
学习就是为神经网络的所有层找到一组正确的权重值，训练神经网络主要围绕以下四个方面。

• 层，多个层组合成网络（或模型）。
• 输入数据和相应的目标。
• 损失函数，即用于学习的反馈信号。
• 优化器，决定学习过程如何进行
• 多个层链接在一起组成了网络，将输入数据映射为预测值。然后损失函数将这些预测值与目标进行比较，得到损失值，用于衡量网络预测值与预期结果的匹配程度。优化器使用这个损失值来更新网络的权重。
  

从机器学习scikit-learn到深度学习pytorch

pytorch概述

what-pytorch

PyTorch是由Facebook的AI研究团队开发的基于 Python 的科学计算包，是一个高灵活性、速度快的深度学习平台。基于以下两个目的而开发的python深度学习框架：

• pytorch和Numpy许多功能类似，无缝替换NumPy，利用GPU加速神经网络的运算。
• 通过自动微分机制，来让神经网络的实现变得更加容易。
  

why-pytorch

• 简洁易懂：Pytorch的API设计的相当简洁一致。tensor与NumPy功能类似，方便学习。
• 便于调试：Pytorch采用动态图，可以像普通Python代码一样进行调试。
• 强大高效：有丰富的模型组件，可以快速实现想法、运行速度很快。
• 自动求导，GPU加速，资源多arXiv 中新论文的算法大多有 PyTorch 实现
• 感觉PyTorch是在学术界占据主导地位，让科研工作者感到满意，新模型都是PyTorch实现的，工业界的开发者总不能不用最新的算法、模型，只能纷纷转向PyTorch了。【Facebook的pytorch，百度的paddle，谷歌的TensorFlow，华为的mindspore】
  

how-pytorch

• 要理解深度学习，需要熟悉很多简单的数学概念：张量、张量运算、微分、梯度下降等。
• 通过对比numpy学习pytorch ：从 NumPy 到 PyTorch：不仅是数值计算的进阶
  

pytorch概述，代码实现

########################################################## pytorch概述########################################################import torchprint(torch.__version__)  # 2.1.0print("pytorch和Numpy许多功能类似，无缝替换NumPy，利用GPU加速神经网络的运算")print("自动微分机制让神经网络的实现变得容易")# print("#"*56)# dir(torch)# dir(torch.nn)# help(torch.arange)
pytorch模块介绍

1. torch

这个模块是PyTorch的核心模块，提供了多维数组（张量）的操作，这些操作在很多方面类似于NumPy，但可以在GPU上运行以加速计算。

• 张量操作：创建和操作多维数组。
• 数学运算：提供了广泛的数学运算支持，如加法、减法、线性代数运算等。
• CUDA支持：允许张量操作在NVIDIA GPU上运行，显著提高性能。
  

2. torch.nn

这个模块提供了构建神经网络所需的所有构建块。它定义了一系列预制的层，如全连接层、卷积层、激活函数等，以及用于构建自定义网络的工具。

• 预定义层：包括线性层、卷积层、循环层等。
• 激活函数：如ReLU、Sigmoid和Tanh。
• 损失函数：如均方误差、交叉熵等。
• 容器：如nn.Sequential，用于组合多个层。
  

3. torch.optim

优化器在训练过程中用于更新网络权重。torch.optim模块提供了各种优化算法，如SGD、Adam和RMSprop。

• 优化算法：不同类型的优化算法支持不同的训练需求。
• 学习率调整：可以调整学习率以改进训练过程。
  

4. torch.autograd

自动微分是PyTorch的一个核心特性，允许自动计算神经网络中的梯度。这对于实现反向传播至关重要。

• 自动梯度计算：简化了反向传播的实现。
• 动态计算图：即时创建和修改计算图。
  

5. torch.utils.data

这个模块提供了处理和加载数据的工具，是构建高效、可扩展的数据输入管道的关键。

• Dataset：定义了一个数据集接口。
• DataLoader：用于批量加载数据，支持多线程和数据混洗。
  

6. torchvision

虽然不是PyTorch核心库的一部分，但torchvision常用于处理图像数据。它提供了常见的数据集、模型架构和图像转换工具。

• 预训练模型：如ResNet、VGG等。
• 数据集：如CIFAR、ImageNet等。
• 图像转换：进行图像预处理，如裁剪、缩放等。
  

其他与深度学习相关的工具和库，如：

• torchvision：用于计算机视觉任务的数据集和模型。
• torchtext：用于自然语言处理任务的数据集和预处理工具。
• torchaudio：用于音频处理的工具包。
• PyTorch Lightning：一种简化 PyTorch 代码的高层库，专注于研究和实验的快速迭代。
  

2张量

张量是多维数组，目的是把向量、矩阵推向更高的维度。

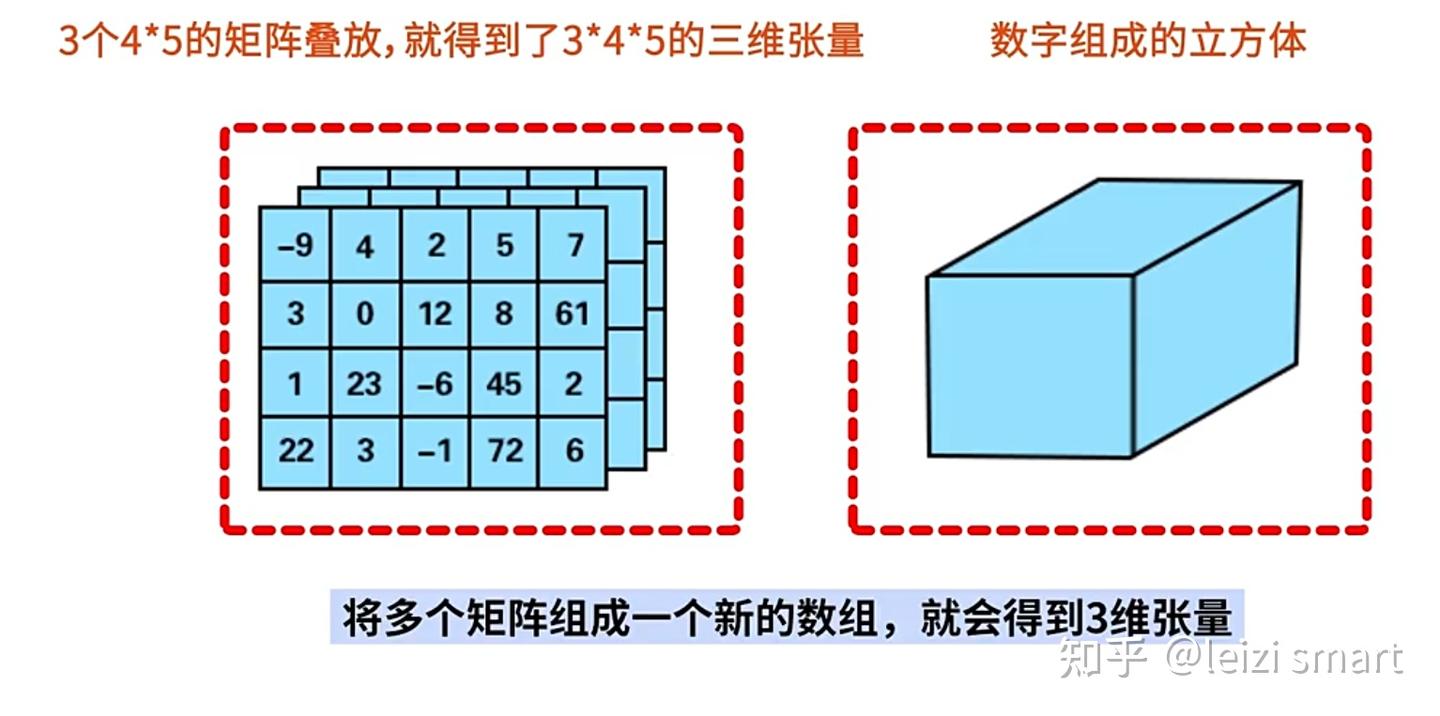
张量的维度：有几层中括号，就是多少维的张量

张量维度	内容
0维张量	标量
1维张量	向量
2维张量	矩阵
3维张量	彩色图像有rgb三个通道
4维张量	视频

实践：

• 张量创建
• 张量属性
• 张量操作：
  
  • 张量创建
  • 数学操作，如加法、乘法
  • 维度变化
  • 广播机制
  • 矩阵svd分解
    

1张量创建代码实现

########################################################## 1张量创建########################################################import torch# torch.randint(0,10,(2,3)) # [low,high),sizetensor1 = torch.rand(2, 3)print("1随机数值在0到1之间，均匀分布的张量:")print(tensor1)tensor2 = torch.zeros(2, 3)print("2全零张量:")print(tensor2)tensor3 = torch.ones(2, 3)print("3全一张量:")print(tensor3)import numpy as npnumpy_array = np.array([1, 2, 3])tensor4 = torch.from_numpy(numpy_array)print("4NumPy数组创建张量:")print(tensor4)list_data = [4, 5, 6]tensor5 = torch.tensor(list_data)print("5列表创建张量:")print(tensor5)

2张量属性代码实现

################################################################### 2张量属性：维度，形状，数据类型，存储和计算设备# 张量6个属性# data: 被包装的 Tensor# ndim: 张量的维度，有几层中括号，就是多少维的张量# dtype: 张量的数据类型，如 torch.FloatTensor，torch.cuda.FloatTensor# shape: 张量的形状。如 (2,3)# device: 张量所在设备 (CPU/GPU)，GPU 是加速计算的关键# grad: data的梯度。# requires_grad: 指示是否需要梯度，并不是所有的张量都需要计算梯度。################################################################### 张量操作：张量支持各种数学操作，如加法、乘法、卷积、池化等import torchscalar = torch.tensor(5)print("零阶张量（标量）:")print(scalar)vector = torch.tensor([1, 2, 3])print("一阶张量（向量）:")print(vector)matrix = torch.tensor([[1, 2, 3], [4, 5, 6]])print("二阶张量（矩阵）:")print(matrix)# 创建一个从0到5，步长为1，形状为(2, 3),数据类型为float32的类型张量tensor = torch.arange(6, dtype=torch.float32).reshape(2, 3)print(tensor)# 输出张量的维度、形状、数据类型、存储设备print("维度 (Number of dimensions):", tensor.dim(), tensor.ndim)print("形状 (Shape):", tensor.shape, tensor.size())print("数据类型 (Data Type):", tensor.dtype)print("存储设备 (Device):", tensor.device)# 类型转换tensor = torch.randint(1,5,(2,3))tensor_float = tensor.float()print(tensor.dtype, tensor_float.dtype)

3.1张量操作：数学操作，如加法、乘法代码实现

################################################################### 3.1张量操作：数学操作，如加法、乘法################################################################### 创建张量tensor1 = torch.tensor([1, 2, 3], dtype=torch.float32)tensor2 = torch.tensor([4, 5, 6], dtype=torch.float32)addition_result = tensor1 + tensor2print("张量加法addition_result:", addition_result)multiplication_result = tensor1 * tensor2print("张量乘法multiplication_result:", multiplication_result)division_result = tensor1 / tensor2print("张量除法division_result:", division_result)squared_tensor = torch.square(tensor1)print("逐元素平方squared_tensor:", squared_tensor)mean_value = torch.mean(tensor1)print("均值mean_value:", mean_value)variance = torch.var(tensor1)print("方差variance:", variance)min_value = torch.min(tensor1)print("最小值min_value:", min_value)print("最小值min_value的位置（索引）:", torch.argmin(min_value).item())

3.2张量操作：访问张量中的元素，索引和切片，代码实现

################################################################### 3.2张量操作：访问张量中的元素，索引和切片##################################################################tensor3 = torch.arange(6, dtype=torch.float32).reshape(2, 3)# 访问张量中的特定元素element = tensor3[1, 1].item()print(element)element = tensor3[1, 1]print(element)# 张量索引和切片element = tensor3[1]  # 获取索引为2的元素print(element)sliced_tensor = tensor3[:,1:2]  # 切片获取部分张量print(sliced_tensor)

3.3张量操作：维度变化，代码实现

################################################################### 3.3张量操作：维度变化################################################################### 增加新的维度，在0轴前添加新维度tensor = torch.arange(4, dtype=torch.float32).reshape(2, 2)new_tensor = tensor.unsqueeze(0)print(new_tensor, new_tensor.shape)# 删除维度，删除0轴维度new_tensor = new_tensor.squeeze(0)print(new_tensor, new_tensor.shape)# 更改张量的形状new_tensor = tensor.view(1, 4)  # 改为形状为(1, 4)的张量print(new_tensor, new_tensor.shape)# 按0维分成两块tensor1, tensor2 = torch.split(tensor, split_size_or_sections=1, dim=0)print(tensor1, tensor2)# 沿着新的轴（0轴）叠加stacked_tensor = torch.stack((tensor1, tensor2), dim=0)print(stacked_tensor)

3.4张量操作：广播机制，代码实现

################################################################### 3.4张量操作：广播机制# Pytorch的广播规则和numpy是一样的:广播要满足两个条件：# 每一个张量只有有一个一维的维度# 满足右对齐，m*n * 1*n; m*1 * 1*n##################################################################tensor1 = torch.tensor([1,2,3])tensor2 = torch.tensor([[0,0,0],[1,1,1],[2,2,2]])print(tensor1 + tensor2)

3.5张量操作：矩阵svd分解，代码实现

################################################################### 3.5张量操作：矩阵svd分解# svd分解可以将任意一个矩阵分解为一个正交矩阵u,一个对角阵s和一个正交矩阵v.t()的乘积# svd常用于矩阵压缩和降维##################################################################a=torch.tensor([[1.0,2.0],[3.0,4.0],[5.0,6.0]])u,s,v = torch.svd(a)print(u,"\n")print(s,"\n")print(v,"\n")print(u@torch.diag(s)@v.t())

注意

t.tensor和t.Tensor的区别

代码实现

import torch as t#使用小写的tensor函数 #根据传入的整型数据，创建整型的张量a = t.tensor([1, 2, 3, 4, 5])print(a)        # tensor([1, 2, 3, 4, 5])print(a.type()) # torch.LongTensor#使用大写的tensor类，会创建浮点类型b=t.Tensor([1, 2, 3, 4, 5])print(b)        # tensor([1., 2., 3., 4., 5.])print(b.type()) # torch.FloatTensor

3激活函数

常见激活函数

激活函数

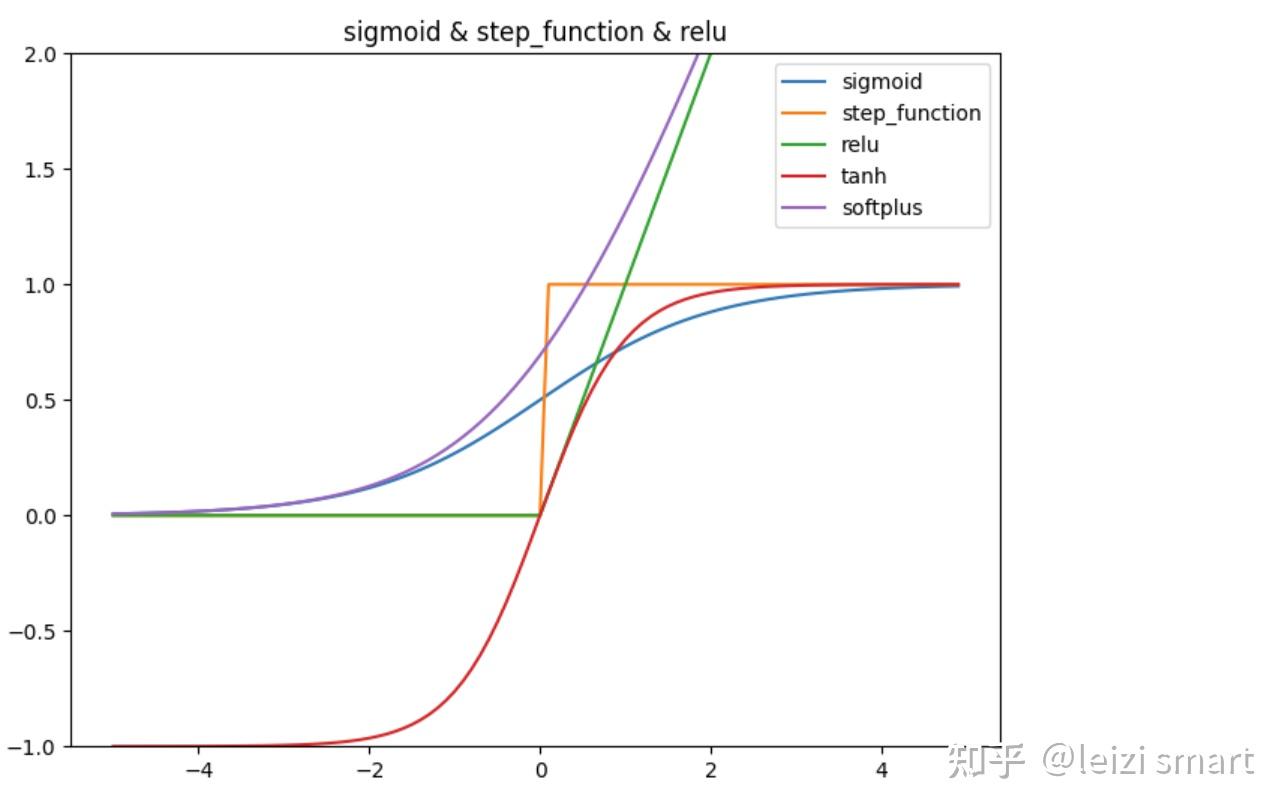
手动实现激活函数，代码实现

import numpy as npimport matplotlib.pylab as pltdef sigmoid(x):    return 1 / (1 + np.exp(-x))def step_function(x):    return np.where(x > 0, 1, 0) #np.array(x > 0, dtype=int)def relu(x):    return np.maximum(0, x)def tanh(x):    return np.tanh(x)def softplus(x):    return np.log(1 + np.exp(x))X = np.arange(-5.0, 5.0, 0.1)Y1 = sigmoid(X)Y2 = step_function(X)Y3 = relu(X)Y4 = tanh(X)Y5 = softplus(X)plt.figure(figsize=(8, 6))plt.plot(X, Y1, label="sigmoid")plt.plot(X, Y2, label="step_function")plt.plot(X, Y3, label="relu")plt.plot(X, Y4, label="tanh")plt.plot(X, Y5, label="softplus")plt.ylim(-1, 2)plt.title('sigmoid & step_function & relu')plt.legend()plt.show()

pytorch中的激活函数

调用pytorch中的激活函数，代码实现

import torchimport matplotlib.pyplot as plt# 定义绘制激活函数图表的函数def plot_activation_function(ax, function, name):    x = torch.linspace(-5, 5, 100)    y = function(x).numpy()    ax.plot(x.numpy(), y, label=name)    ax.set_title(name + ' Activation Function')    ax.set_xlabel('Input')    ax.set_ylabel('Output')    ax.grid(True)    ax.legend()# 创建一个包含多个子图的画布fig, axes = plt.subplots(1, 3, figsize=(18, 6))  # 1行，3列# 可视化不同的激活函数# ReLU 激活函数plot_activation_function(axes[0], torch.nn.ReLU(), 'ReLU')# Sigmoid 激活函数plot_activation_function(axes[1], torch.nn.Sigmoid(), 'Sigmoid')# Tanh 激活函数plot_activation_function(axes[2], torch.nn.Tanh(), 'Tanh')# 调整布局并显示图像plt.tight_layout()plt.show()

4自动求导

• 标量梯度计算
• 非标量梯度计算
• 利用自动微分和优化器求最小值
• 求偏导数
• 具体参考：优化方法-梯度下降法
  

1标量梯度计算，代码实现

################################################################### 梯度计算：1标量的反向传播##################################################################import matplotlib.pyplot as pltimport numpy as npimport torch # 1 准备数据 y=f(x)x = np.linspace(1, 10, 200)  # 生成0到5之间的100个数据a, b, c = 1, -8, 12y = a * x ** 2 + b * x + cdy = 2* a * x  + b point_x = 6point_y = 0k = 2*a*point_x + btangent_y = k*(x - point_x) + point_y# 2 绘制图形plt.figure(figsize=(8, 6))plt.plot(x, y, label='y')  # 函数画图# plt.plot(x, dy, label='dy')  # 导数画图plt.scatter(point_x, point_y, color='red') # 点画图plt.plot(x, tangent_y, label='tangent_y')  # 切线画图plt.axvline()  # 绘制横线plt.axhline()  # 绘制竖线plt.title("函数，切线", fontproperties="SimHei", fontsize= 18)plt.grid()plt.legend()  # 添加图例plt.show()# f(x) = a*x**2 + b*x + cx = torch.tensor(6.0, requires_grad = True) # x需要被求导a = torch.tensor(a)b = torch.tensor(b)c = torch.tensor(c)y = a*x**2 + b*x + cy.backward()# backward 通常在一个标量张量上调用，求得的梯度将存在对应自变量张量的grad属性下dy_dx = x.gradprint("梯度值", dy_dx) # 输出梯度值，应该为4print(x.grad==2*a*x + b) #验证# 梯度清零，如果没有这一步结果就会加累上之前的梯度值，变为[4]x.grad.zero_()y = a*torch.pow(x,2) + b*x + cy.backward()print("梯度值", x.grad)

2非标量梯度计算，代码实现

################################################################### 梯度计算：2非标量的反向传播,传入一个和它同形状的gradient参数张量##################################################################import numpy as npimport torch# f(x) = a*x**2 + b*x + cx = torch.ones((2,2), requires_grad=True)a = torch.tensor(2.0)b = torch.tensor(-8.0)c = torch.tensor(12.0)y = a*torch.pow(x,2) + b*x + cgradient = torch.ones_like(x)   # 保留 x_data 的属性y.backward(gradient = gradient)x_grad = x.gradprint("x_grad:\n",x_grad)

3利用自动微分和优化器求最小值，代码实现

################################################################### 梯度计算：3利用自动微分和优化器求函数最小值##################################################################import torch# f(x) = a*x**2 + b*x + cx = torch.tensor(1.0, requires_grad = True) # x需要被求导a = torch.tensor(2.0)b = torch.tensor(-8.0)c = torch.tensor(12.0)optimizer = torch.optim.SGD(params=[x],lr = 0.01)def f(x):    result = a*torch.pow(x,2) + b*x + c    return(result)for i in range(500):    optimizer.zero_grad()    y = f(x)    y.backward()    optimizer.step()print("利用自动微分和优化器求函数最小值y=",f(x).data,";","x=",x.data)

4求偏导数，代码实现

# (a) --> (x)#     \ /     \#      .        (z)#     / \     /# (b) --> (y)# x = 2a + 3b# y = 5a^2 + 3b^3# z = 2x + 3y# dz/da = dz/dx * dx/da + dz/dy * dy/da#       = 2 * 2 + 3 * 10a#       = 4  + 30a# a = 3.5, dz/da = 64 import torch a = torch.tensor(2.0, requires_grad=True)b = torch.tensor(1.0, requires_grad=True)x = 2*a + 3*by = 5*a*a + 3*b*b*bz = 2*x + 3*yz.backward()print(a.grad) # tensor(64.)
5计算加速

PyTorch和NVIDIA GPU以及CUDA的关系：

• PyTorch作为深度学习框架提供了算法支持；
• NVIDIA GPU提供了高性能的并行计算能力；
• CUDA（NVIDIA提供的并行计算平台和编程模型）利用NVIDIA GPU的并行计算能力加速深度学习模型的训练和推理运算；
  

GPU加速，代码实现

import numpy as npimport torchimport time# 创建随机矩阵n = 500np_matrix_a = np.random.rand(n, n)np_matrix_b = np.random.rand(n, n)torch_matrix_a = torch.rand(n, n)torch_matrix_b = torch.rand(n, n)# NumPy矩阵乘法start_time = time.time()np_result = np.dot(np_matrix_a, np_matrix_b)numpy_time = time.time() - start_time# PyTorch矩阵乘法（CPU）start_time = time.time()torch_result_cpu = torch.mm(torch_matrix_a, torch_matrix_b)torch_cpu_time = time.time() - start_time# PyTorch矩阵乘法（GPU）if torch.cuda.is_available():    # 将数据移到GPU    torch_matrix_a = torch_matrix_a.to('cuda')    torch_matrix_b = torch_matrix_b.to('cuda')    start_time = time.time()    torch_result_gpu = torch.mm(torch_matrix_a, torch_matrix_b)    torch_gpu_time = time.time() - start_timeelse:    torch_gpu_time = -1    print("未支持CUDA")print(f"NumPy 矩阵乘法耗时: {numpy_time} 秒")print(f"PyTorch 矩阵乘法（CPU）耗时: {torch_cpu_time} 秒")print(f"PyTorch 矩阵乘法（GPU）耗时: {torch_gpu_time} 秒")

NumPy 矩阵乘法耗时: 0.0058977603912353516 秒
PyTorch 矩阵乘法（CPU）耗时: 0.003974199295043945 秒
PyTorch 矩阵乘法（GPU）耗时: 0.00033020973205566406 秒

总结与参考

总结

• 深度学习概述
  
  • 深度学习原理
  • pytorch概述
    
• 张量
  
  • 张量创建
  • 张量属性
  • 张量操作：张量创建；数学操作如加法乘法；维度变化；广播机制；矩阵svd分解
    
• 激活函数
  
  • ReLU，sigmoid，tanh
    
• 自动求导
  
  • 标量；非标量
    
• 计算加速
  
  • GPU加速
    

希望能收到您的反馈！！！2023年11月30日15:11:42

参考

• 机器学习scikit-learn
• 1分钟快速理解张量 | Tensor - 产品经理的人工智能学习库
  

学习资料

书籍

• 李沐动手深度学习
• 《Python深度学习》-微信读书