经管之家App
让优质教育人人可得
立即打开
丘成桐先生认为“数学在人工智能和大数据领域发挥重要作用，不仅是算法和技术的核心基础，更是理解大数据深层含义的关键。许多曾被认为抽象的数学理论，如今已经成为解决科学、技术、经济与社会核心问题的具体工具。”丘先生这句关于AI基础的论断，如今为深陷“幻觉”泥潭的大语言模型指明方向。当AI在医疗诊断中把肺炎的咳嗽、发热、呼吸困难误判为感冒，轻描淡写地建议“多喝水休息”时，患者可能错失最佳治疗窗口；当律师提交的AI生成法律文书中赫然出现“《民法典》第1234条”这样的虚构法条时，不仅面临法庭罚款，更让本就紧张的司法资源白白浪费；当科研人员循着模型编造的《量子面条理论》参考文献追踪研究时，宝贵的学术精力正被引入不存在的歧途。
这些看似孤立的幻觉现象，实则暴露了生成模型的底层缺陷：其知识空间如同微分几何中带有“奇异点”的流形 - 那些违背逻辑事实的错误信息隐藏在曲率突变的异常区域，而模型生成内容的过程，恰似缺乏严谨导航时误入这些陷阱的路径偏差。当AI的概率迷宫遇上微分几何的逻辑灯塔，丘先生所创立的几何分析能否成为校准认知偏差的数学罗盘？跨域数学与人工智能的对话，或许正孕育着消除AI幻觉的根本性突破。
图1. Sora产生短视频中的幻觉。
所谓“AI幻觉”就是AI模型输出的虚假、不准确或不符合事实的信息，这些信息通常看起来具有说服力，但实际上是错误的或者与现实世界不符的（违反物理定律、生物定律等等）。例如图1中，Sora生成的短视频，看上去非常逼真，但是有很多荒谬之处。例如“草坪上的小狗”视频，小狗一会儿是3只，一会儿是4只，这显然违反了生物和物理定律；“杯子的红酒”视频中，酒杯还没有还没有倾倒，红酒就已经泼洒出来，违反了流体力学；“四足蚂蚁”视频违反了生物定律等等。图2是文生图中常见的幻觉，当我们给出提示词“兔子和乌龟”，模型生成龟身兔头的生物。这是基于令牌（Token）的生成模型常见的幻觉。反之，所谓“想像”就是AI模型输出的真实、准确和符合事实的信息，满足所有的物理定律、生物定律等自然法则。这些生成的数据可能并不完全与训练样本重合，但是符合训练集的统计规律。
图2. 文生图的幻觉，rabbit and turtle.
图 3. 弥勒佛曲面和其在平面上的嵌入。
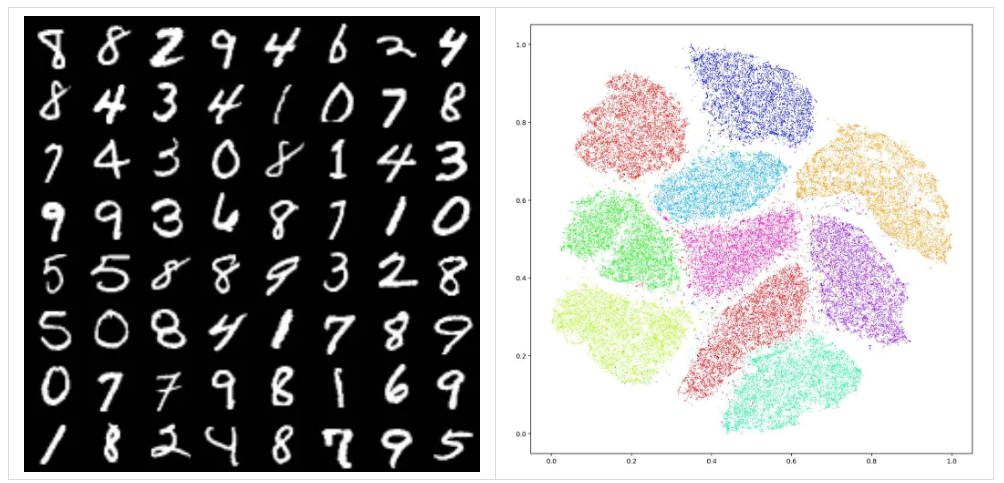
图 4. LeCunn的MNIST 训练集；Hinton的t-SNE的降维。
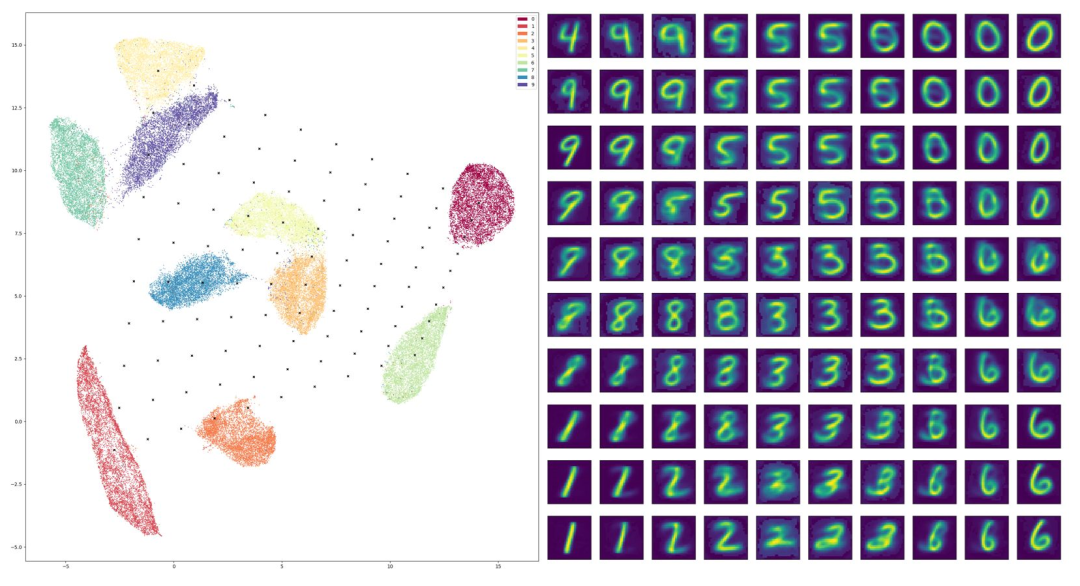
图 5. UMap 嵌入和采样。
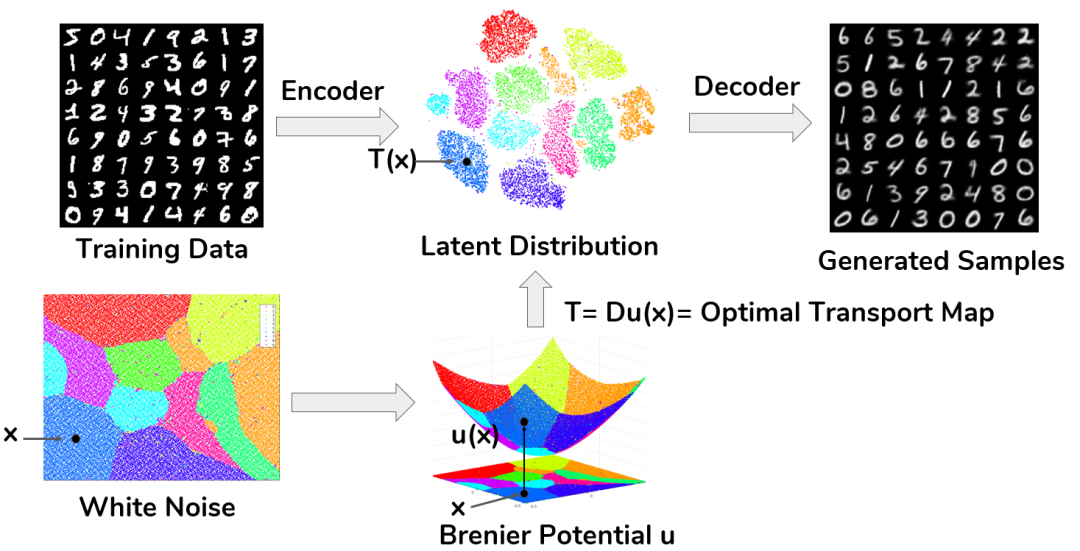
图6. 生成模型的框架。
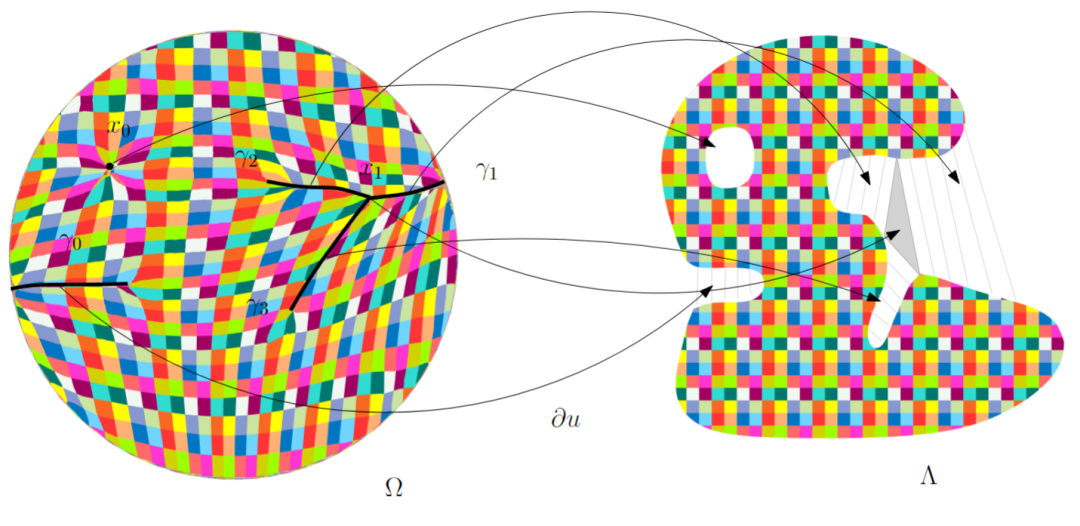
图 7. Figalli给出的反例，传输映射不连续。
图 8. 闵可夫斯基问题：凸曲面由高斯曲率所决定，可归结为球面最优传输。
早在1993年，丘成桐先生就提出了上百个微分几何领域的开放问题，其中一个就是发明数值方法求解闵可夫斯基（Minkowski）问题。这个问题是凸几何中的刚性问题：如何通过高斯曲率来恢复一个凸曲面的形状。这个问题可以转化为球面最优传输问题，最终也归结为求解球面蒙日-安培方程。丘先生指导笔者团队在2013年通过几何变分法求解欧式空间的最优传输问题，在2019年发展了球面最优传输问题的求解算法，从而解决了这个公开问题。用这种方法，我们可以精确求出奇异集合，从而准确求得数据概率分布支集的边界。
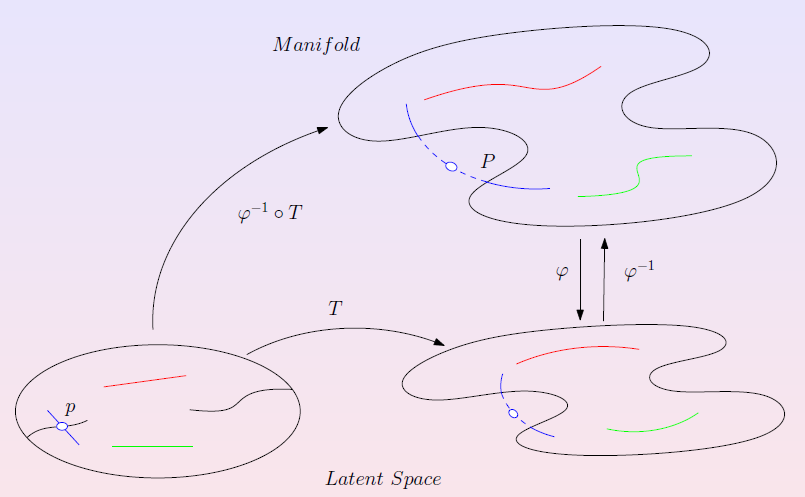
图 9. 数据流形边缘检测实验设计。
图 10. 人脸图像流形边界附近的人脸。
Sora生成的红酒视频中，酒杯有两种稳恒态：直立状态和水平躺倒状态，还有一个从直立到倾倒的过渡态。我们很容易从稳态中收集样本，因此Sora产生了稳态图像；从过渡态收集样本非常困难，因此Sora没有生成过渡态图像。但是对应人类感知而言，过渡态是理解物理过程的关键。稳恒态对应的概率分布支集的边界是过渡态，过渡态的样本生成至关重要。
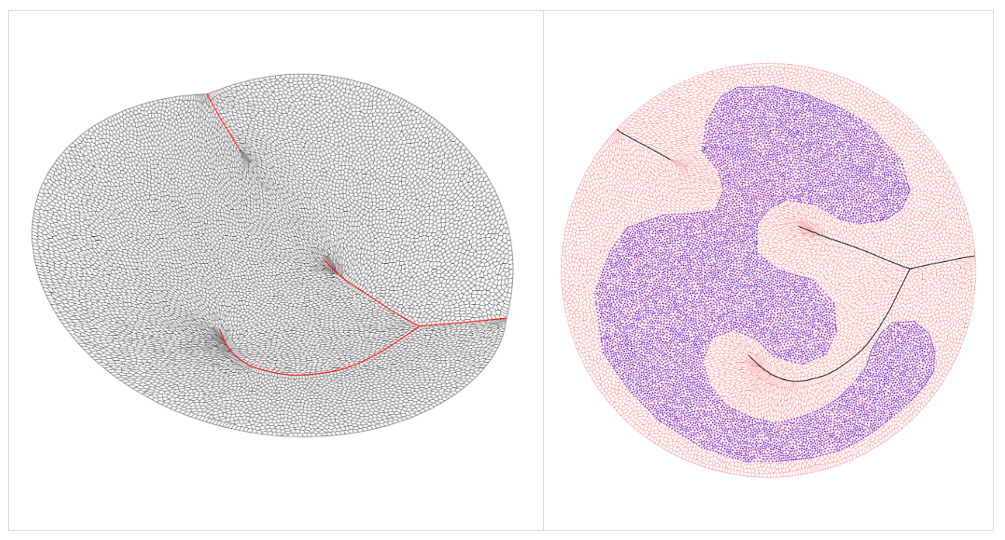
图 11. Brenier势能函数的非光滑点对应着最优传输映射的奇异集合，对应着数据分布支集的边界。
目前最为流行的生成模型是基于扩散过程的模型。对于任意的数据分布，所谓的熵流对应的就是扩散过程，在扩散过程中概率分布的熵单调递增，最后到达最大值。给定期望和方差的概率分布中，熵最大者为高斯分布。因此，扩散过程就是给出从数据分布到高斯分布的传输映射。扩散过程可以用郎之万动力学(Langevin dynamics)来模拟，即每个粒子加上白噪声随机游走，即可到达高斯分布。扩散模型的好处是不需要显示表达概率密度，所有粒子可以并行独立随机游走。但是其缺陷在于模糊了概率分布支集的边界，最后求得的传输变换（逆扩散）给出的数据分布精度较低，无法得到确切支集边界信息，生成真实数据分布之外的样本，形成幻觉。这再次证明了数据分布支集边界具有生物学意义，在真实图像生成的任务中不容随意穿越。
图12. 通过掌握数据分布支集的边界，我们可以精确地合成跨物种生物。上排：真实的生物图像；下排，从左到右：介于狗和猫、狗和豹、狗和狐狸之间的生物。（汪展鹏作）
如图11所示，我们用几何变分方法计算最优传输映射，求得Brenier势能函数。通过势能函数的非光滑点（法向量突变的点），我们可以求得传输映射的奇异集合（右帧黑色曲线），奇异集合对应着数据概率分布支集的边界。如图12所示， 通过掌握数据分布支集的边界，我们可以精确地合成跨物种生物。图中上排是真实的生物图像。我们求出不同物种图像的数据分布边缘，然后在猫的分布边缘和狗的分布边缘之间找到最短连线，沿着连线生成介于猫和狗之间的图像，如左下角所示。同样的，我们可以生成狗和豹、狗和狐狸之间的生物。这显示了这种方法的想像力和泛化能力。
在目前流行的文生图应用中，图像生成模型和大语言模型相结合，图像隐空间与语义隐空间之间建立映射，可以从语言提示映到图像隐空间，从而根据提示生成图像。人们将语言模型的令牌概念引入图像领域，将图像分解成很多子图像作为令牌，然后将令牌作为样本进行训练。如图2所示，虽然生成的每个令牌看上去非常逼真，但是令牌之间的概率分布没有精确学会，因此虽然局部上生成质量很高，但是整体上严重失真。这需要我们加强令牌间联合概率分布的学习，即令牌上下文概率分布的学习。我们可以将每个令牌的所有可能视为一个令牌数据流形，所有令牌组成的图像构成图像数据流形，图像数据流形为令牌数据流形的乘积流形，令牌间的联合概率分布定义在乘积流形之上，从而构造层级学习结构，以减少幻觉。
生成式大模型可以从微分几何观点用流形分布原理来解释：每个数据样本被视为高维背景空间中的一个点；所有数据样本的集合可以被描述为背景空间中的点云，包含在某个低维数据流形中，流形维数远远低于背景空间维数；同时数据样本集合在数据流形上具有特定的概率分布。大模型的训练过程可以用微分几何形式归纳为：1) 学习数据流形的拓扑几何结构; 2)学习数据在流形上的概率分布。大模型的推理过程归纳为在数据分布上采样。数据流形的拓扑几何结构通常用编码、解码映射来表示；Whitney流形嵌入理论保证映射的存在性，UMap算法仿照了定理的证明；数据概率分布通常用传输映射来表示：传输映射将已知的高斯白噪声映射到数据分布。
深度神经网络可以万有逼近任意多元连续函数，目前的各种深度神经网络CNN, DNN, Transformer都是Kolmogorov-Arnold定理的算法实现。K-A定理证明了任意多变量、连续函数都可以用单变量函数和加法算子的有限次复合来表示；但是K-A方法无法直接表示不连续函数；目前AI生成模型中的编码、解码映射和传输映射由深度神经网络来表示。但是菲尔兹奖得主Villani和Figalli的工作指出传输映射非连续，目前AI生成模型无法准确学会。概率分布支撑集合边界代表自然定律的限制，往往具有物理、生物或者数学的意义，在自然界中不可逾越。传统生成模型的穿越行为，造成了幻觉。扩散模型将数据分布变成高斯分布，粗糙近似，模糊了数据分布支撑集合的边界信息，引发模式混淆和幻觉。
丘先生与笔者团队提出的AE-OT（AutoEncoder-OptimalTransport）生成模型，有望从根本上克服了模式坍塌、模式混淆和幻觉问题。AE-OT生成模型解耦了数据流形的拓扑结构学习任务和数据概率分布的学习任务，前者用Auto-Encoder等AI方法，后者的实现运用了我们发明的几何变分方法求解最优传输问题。AE-OT能够精确求得非连续的概率分布传输变换（而非粗糙近似），严格确定了概率分布支撑集合的边界。AE-OT模型自身在生成过程中避免穿越概率分布支撑集的边界，从理论上保证杜绝产生谬误，防止幻觉。AE-OT模型可以与现有生成模型结合，提供精确的数据概率分布信息，当生成过程接近分布边缘时提出警告，防范幻觉。
最优传输理论寻求最经济的方法实现概率分布之间的变换。Brenier极分解定理断言任何传输变换都可以分解成最优传输变换与保勒贝格体积的变换，因此最优传输变换决定了整个变换的连续性。Brenier定理将最优传输问题归结为求解强烈非线性的蒙日-安培方程。丘成桐先生于1993年提出了100多个微分几何的开放问题，其中包括求解闵可夫斯基问题，等价于解球面蒙日-安培方程。2013年丘先生与顾教授团队用几何变分原理提出了蒙日-安培方程的求解算法；2019年解决了闵可夫斯基问题-最优传输问题。这个理论结果被直接用于提高AI生成模型的质量。
历史的发展会让我们看到，几何分析正在为生成式AI提供严谨坚实的数学基础，有了因果逻辑的指导，概率模型有望从根源上消除AI幻觉。
全部版块
我的主页
收藏
原文作者： 老顾谈几何
原文链接： https://mp.weixin.qq.com/s/vgCN6PfEaqdw2-51FyiB6Q
来源： 微信公众号
扫码加好友，拉您进群
