推荐理由

本文提出了一种新的室内 RSSI 无线电地图重建算法，通过结合低秩矩阵理论，通过少量几何网格点即可补全 RSSI 网格网络，大幅减少数据采集成本，同时融合两种特征点并按定位精度加权，进一步优化了模型可靠性。

正文

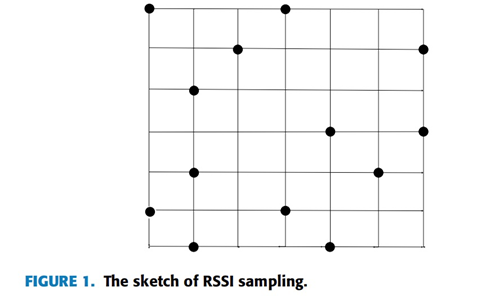
假设目标定位区域为矩形区域，内部分布有m×n个用于 RSSI 采样的指纹点，则每个AP会对应一个m×n维度的信号强度采样矩阵。实际应用中，若仅采集少量 RSSI 采样点，需通过低秩矩阵填充恢复整个目标区域的二维 RSSI 矩阵。如图1所示，实心点表示已采集RSSI的采样网格点，其余未采样点需通过低秩矩阵理论填充。

首先将目标区域的完整RSSI矩阵定义为X，所有网格点总数为N；实际采样中仅选取s个网格点（s<N）进行RSSI采集，形成的不完整矩阵（含大量未采样点）定义为观测矩阵B。为建立B与X的关联，基于仿射矩阵的秩最小化理论（对于 RSSI 无线电地图，由于“相邻位置的RSSI值具有强相关性”（空间连续性），完整的X通常是低秩矩阵（秩远小于矩阵的维度）），构建如下优化问题：

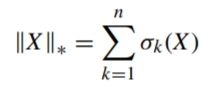
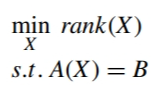
为了避免直接求解秩最小化的NP难问题，使用核范数替代秩，将原组合优化问题转化为凸松弛优化问题。

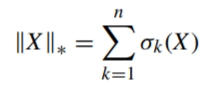
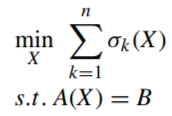
若直接对X优化，需同时调整m×n个元素，计算量极大，因此对完整矩阵X进行奇异值分解（SVD）：

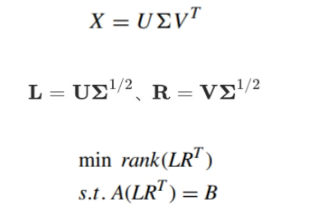
由于L和R可能存在多组解，通过最小化弗罗贝尼乌斯范数对其进行优化

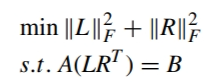
此外，考虑到采样的 RSSI 数据可能存在误差，且定位区域的矩阵未必完全满足低秩特性，将约束模型转化为无约束模型，引入重构误差权重矩阵ω

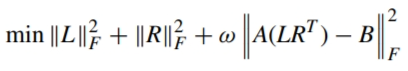
最后通过以下交替迭代步骤求解矩阵L和R：

1）采用最小二乘法计算矩阵X的初始值X0及其可能的分解矩阵，随机选取一组X

的分解矩阵作为L和R的初始值；

2）固定L，求解R；

3）固定R，求解L；

4）重复步骤 2 和 3，直至式（8）计算的目标函数收敛。

几何空间网格点填充完成后，RSSI 空间信号特征点与新填充的几何特征点之间会存在重叠点（同一位置同时属于两类特征点）。对于每个重叠点，存在两个 RSSI 值：采样得到的 RSSI 值（实测值）与填充得到的 RSSI 值（估计值），两者的差值定义为：

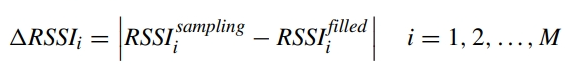
实际应用中，重叠点的 RSSI 值采用采样值（实测值更可靠），同时利用上述 RSSI 差值为非重叠填充几何特征点（仅属于几何空间网格点的填充点）分配权重，权重分配的核心逻辑是 “RSSI 差值越小，填充精度越高，对应非重叠填充点的权重越大”，以此提升模型对高可信度填充点的依赖，优化无线电地图的整体精度具体计算如下：

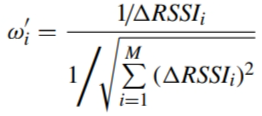
所有权重计算完成后，找出其中的最大值，并以该最大值为基准对权重进行归一化重新计算，确保权重范围在 0-1 之间，便于后续模型融合：

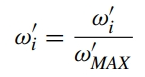
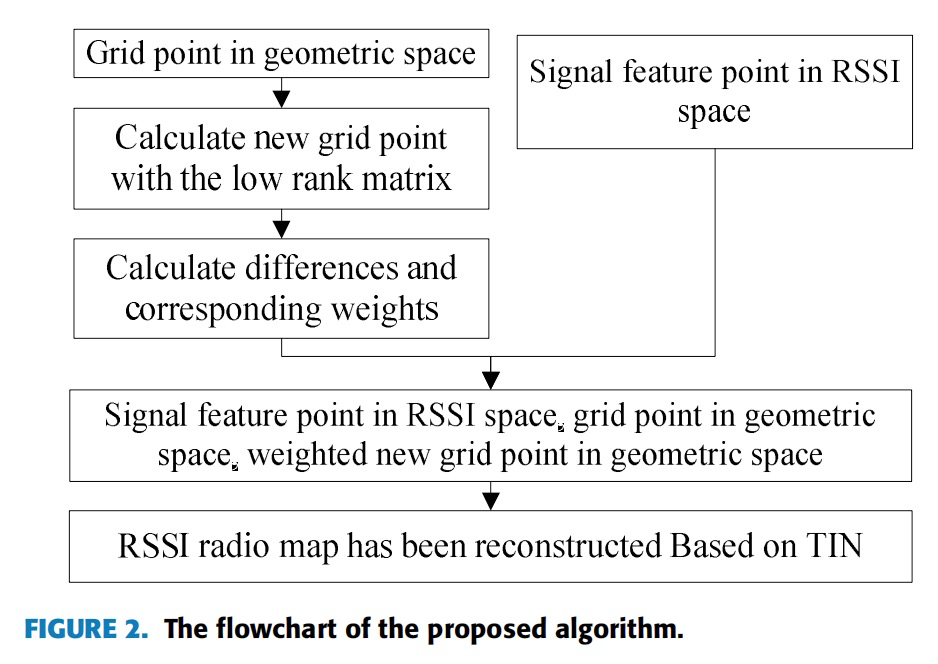
最终，通过 RSSI 空间信号特征点、几何空间网格点以及经权重分配的几何空间新填充网格点，完成 RSSI 经验模型的重构。所提算法的流程图如图 2 所示：

原文链接： https://ieeexplore.ieee.org/abstract/document/8543591

推荐学习书籍 《CDA一级教材》适合CDA一级考生备考，也适合业务及数据分析岗位的从业者提升自我。完整电子版已上线CDA网校，累计已有10万+在读~ !

免费加入阅读：https://edu.cda.cn/goods/show/3151?targetId=5147&preview=0