

贝叶斯回归预测是一种基于贝叶斯统计理论的现代预测技术,它将传统的回归分析与概率建模结合起来。与经典的频率主义方法不同,贝叶斯回归将模型参数视为随机变量,通过先验分布表达对参数不确定性的理解。
该方法的核心思路是利用贝叶斯定理,将参数的先验分布与观测数据的似然函数结合,得到参数的后验分布。这个后验分布不仅提供了参数的点估计值,更重要的是全面描述了参数的不确定性。在进行预测时,贝叶斯方法通过积分考虑所有可能的参数值,得出预测分布,从而自然包含了模型参数的不确定性。
贝叶斯回归预测的一个显著优点是其能够量化预测的不确定性,提供完整的概率预测而非单一预测值。它通过预测区间直观展示预测的可信度,这对于风险评估和决策制定至关重要。此外,该方法允许融入先验知识,在小样本情况下表现尤为稳定。
实际应用中,贝叶斯回归广泛应用于金融风险管理、医疗预后预测、工程可靠性分析等领域,为决策者提供既包含最佳估计又明确表征不确定性的全面预测信息。
% 贝叶斯线性回归预测 - 兼容旧版本MATLAB
% 使用正态-逆伽马共轭先验
clc;close all;clear all;warning off;%清除变量
%% 生成模拟数据
% rng(42); % 设置随机数种子,保证结果可重现
n = 100; % 数据点数量
x = linspace(-3, 3, n)'; % 输入特征
% 真实参数
true_beta0 = 1.5; % 截距
true_beta1 = 2.0; % 斜率
true_sigma2 = 0.5; % 噪声方差
% 生成带噪声的观测数据
y = true_beta0 + true_beta1 * x + sqrt(true_sigma2) * randn(n, 1);
%% 设置先验分布参数
% 对于系数 beta = [beta0; beta1] ~ N(mu0, Sigma0)
mu0 = [0; 0]; % 先验均值
Sigma0 = [10, 0; 0, 10]; % 先验协方差矩阵
% 对于方差 sigma2 ~ InvGamma(a0, b0)
a0 = 2; % 逆伽马分布形状参数
b0 = 1; % 逆伽马分布尺度参数
%% 贝叶斯后验分布计算
% 设计矩阵
X = [ones(n,1), x];
% 计算后验分布参数
% 系数后验: beta | y, X, sigma2 ~ N(mu_n, Sigma_n)
% 方差后验: sigma2 | y, X ~ InvGamma(a_n, b_n)
%%%%
加我q1579325979获取完整代码
%%%
a_n = a0 + n/2;
b_n = b0 + 0.5 * (y'*y + mu0'*Sigma0_inv*mu0 - mu_n'*inv(Sigma_n)*mu_n);
fprintf('后验分布参数:\n');
fprintf('系数后验均值: [%.3f, %.3f]\n', mu_n(1), mu_n(2));
fprintf('方差后验参数: a_n=%.3f, b_n=%.3f\n', a_n, b_n);
%% 后验预测分布
x_new = linspace(-4, 4, 200)'; % 新预测点
X_new = [ones(length(x_new),1), x_new];
% 预测分布的均值和方差
y_pred_mean = X_new * mu_n; % 预测均值
y_pred_var = diag(X_new * Sigma_n * X_new') + b_n/(a_n-1); % 预测方差
y_pred_std = sqrt(y_pred_var); % 预测标准差
% 95%预测区间
y_pred_lower = y_pred_mean - 1.96 * y_pred_std;
y_pred_upper = y_pred_mean + 1.96 * y_pred_std;
%% 绘图展示结果 - 兼容旧版本
figure('Position', [100, 100, 1200, 800]);
% 子图1: 数据拟合和预测
subplot(2,2,1);
hold on;
% 绘制原始数据点 - 兼容版本
scatter(x, y, 40, 'b', 'filled', 'MarkerEdgeColor', 'k');
% 绘制真实关系
plot(x, true_beta0 + true_beta1*x, 'r-', 'LineWidth', 3, 'DisplayName', '真实关系');
% 绘制预测均值
plot(x_new, y_pred_mean, 'g-', 'LineWidth', 3, 'DisplayName', '贝叶斯预测');
% 绘制预测区间 - 使用patch函数替代fill,兼容性更好
patch([x_new; flipud(x_new)], [y_pred_lower; flipud(y_pred_upper)], ...
'g', 'FaceAlpha', 0.2, 'EdgeColor', 'none', 'DisplayName', '95%预测区间');
xlabel('输入 x');
ylabel('输出 y');
title('贝叶斯线性回归预测');
legend('show', 'Location', 'northwest');
grid on;
hold off;
% 子图2: 参数后验分布
subplot(2,2,2);
hold on;
% 从后验分布中采样
n_samples = 5000;
beta_samples = mvnrnd(mu_n, Sigma_n, n_samples);
% 绘制截距的后验分布
[n1, centers1] = hist(beta_samples(:,1), 50);
bar(centers1, n1/trapz(centers1, n1), 'FaceColor', 'blue', 'EdgeColor', 'none', 'FaceAlpha', 0.7);
% 绘制斜率的后验分布
[n2, centers2] = hist(beta_samples(:,2), 50);
bar(centers2, n2/trapz(centers2, n2), 'FaceColor', 'red', 'EdgeColor', 'none', 'FaceAlpha', 0.7);
xlabel('参数值');
ylabel('概率密度');
title('参数后验分布');
legend('截距 \beta_0', '斜率 \beta_1');
grid on;
hold off;
% 子图3: 方差后验分布
subplot(2,2,3);
% 从逆伽马后验分布采样
sigma2_samples = 1./gamrnd(a_n, 1/b_n, n_samples, 1);
[n3, centers3] = hist(sigma2_samples, 50);
bar(centers3, n3/trapz(centers3, n3), 'FaceColor', 'cyan', 'EdgeColor', 'none', 'FaceAlpha', 0.7);
xlabel('方差 \sigma^2');
ylabel('概率密度');
title('方差后验分布');
grid on;
% 子图4: 参数轨迹图(MCMC采样展示)
subplot(2,2,4);
plot(beta_samples(1:1000,1), beta_samples(1:1000,2), 'b-', 'LineWidth', 0.5);
hold on;
scatter(beta_samples(1:1000,1), beta_samples(1:1000,2), 20, 1:1000, 'filled');
xlabel('截距 \beta_0');
ylabel('斜率 \beta_1');
title('参数后验采样轨迹');
grid on;
sgtitle('贝叶斯线性回归预测分析', 'FontSize', 16, 'FontWeight', 'bold');
%% 预测不确定性分析
fprintf('\n预测不确定性分析:\n');
fprintf('平均预测标准差: %.3f\n', mean(y_pred_std));
fprintf('预测区间平均宽度: %.3f\n', mean(y_pred_upper - y_pred_lower));
%% 输出模型比较信息
fprintf('\n模型比较:\n');
fprintf('真实参数: 截距=%.3f, 斜率=%.3f, 方差=%.3f\n', true_beta0, true_beta1, true_sigma2);
fprintf('贝叶斯估计: 截距=%.3f, 斜率=%.3f, 方差=%.3f\n', mu_n(1), mu_n(2), b_n/(a_n-1));
% 计算预测精度
y_pred_train = X * mu_n;
mse = mean((y - y_pred_train).^2);
fprintf('训练集MSE: %.3f\n', mse);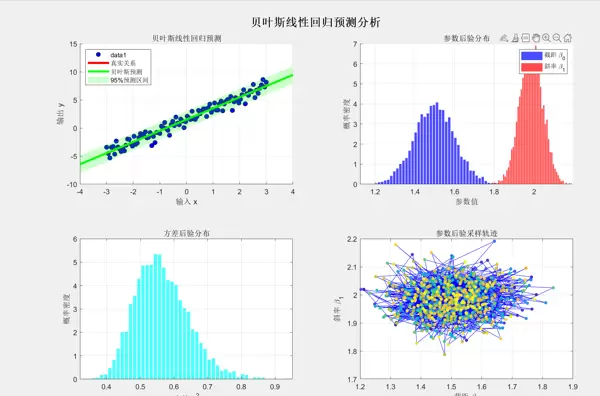
| 中文名称 | 英文全称 | 缩写 | 出现年份 |
|---|---|---|---|
| 遗传算法 | Genetic Algorithm | GA | 1975 |
| 粒子群优化算法 | Particle Swarm Optimization | PSO | 1995 |
| 蚁群优化算法 | Ant Colony Optimization | ACO | 1992 |
| 模拟退火算法 | Simulated Annealing | SA | 1983 |
| 免疫优化算法 | Immune Optimization Algorithm | IA | 1986 |
| 贪婪算法 | Greedy Algorithm | - | 1970 |
| 差分进化算法 | Differential Evolution | DE | 1997 |
| 混合蛙跳算法 | Shuffled Frog Leaping Algorithm | SFLA | 2003 |
| 人工蜂群算法 | Artificial Bee Colony | ABC | 2005 |
| 人工鱼群算法 | Artificial Fish Swarm Algorithm | AFSA | 2002 |
| 萤火虫算法 | Glowworm Swarm Optimization | GSO | 2005 |
| 果蝇优化算法 | Fruit Fly Optimization Algorithm | FOA | 2011 |
| 布谷鸟搜索算法 | Cuckoo Search | CS | 2009 |
| 猴群算法 | Monkey Algorithm | MA | 2008 |
| 免疫网络算法 | Immune Network Algorithm | aiNet | 2000 |
| 水滴算法 | Intelligent Water Drops Algorithm | IWD | 2007 |
| 和声搜索算法 | Harmony Search | HS | 2001 |
| 克隆选择算法 | Clonal Selection Algorithm | CLONALG | 2000 |
| 禁忌搜索算法 | Tabu Search | TS | 1986 |
| 爬山算法 | Hill Climbing | HC | 1940 |
| 引力搜索算法 | Gravitational Search Algorithm | GSA | 2009 |
| 细菌觅食优化算法 | Bacterial Foraging Optimization | BFO | 2002 |
| 蝙蝠算法 | Bat Algorithm | BA | 2010 |
| 邻域搜索算法 | Neighborhood Search | NS | 1960 |
| 变邻域搜索算法 | Variable Neighborhood Search | VNS | 1997 |
| 蜜蜂交配优化算法 | Honey Bees Mating Optimization | HBMO | 2001 |
| 文化基因算法 | Memetic Algorithm | MA | 1989 |
| 烟花算法 | Fireworks Algorithm | FWA | 2010 |
| 思维进化算法 | Mind Evolutionary Algorithm | MEA | 1998 |
| 蜻蜓算法 | Dragonfly Algorithm | DA | 2016 |
| 虚拟力场算法 | Virtual Force Field Algorithm | VFF | 1989 |
| 遗传规划 | Genetic Programming | GP | 1992 |
| 鲸鱼优化算法 | Whale Optimization Algorithm | WOA | 2016 |
| 灰狼优化算法 | Grey Wolf Optimizer | GWO | 2014 |
| 狼群算法 | 2007 | ||
| 鸡群优化算法 | Chicken Swarm Optimization | CSO | 2014 |
| 序号 | 模型名称 | 核心特点 | 适用场景 |
|---|---|---|---|
| 1 | BiLSTM 双向长短时记忆神经网络分类 | 双向捕获序列上下文信息 | 自然语言处理、语音识别 |
| 2 | BP 神经网络分类 | 误差反向传播训练 | 通用分类任务 |
| 3 | CNN 卷积神经网络分类 | 自动提取空间特征 | 图像、视频分类 |
| 4 | DBN 深度置信网络分类 | 多层受限玻尔兹曼机堆叠 | 特征学习、降维 |
| 5 | DELM 深度学习极限学习机分类 | 结合 ELM 与深度架构 | 复杂分类任务 |
| 6 | ELMAN 递归神经网络分类 | 含反馈连接的递归结构 | 时间序列、语音 |
| 7 | ELM 极限学习机分类 | 随机生成隐藏层,快速训练 | 小样本学习 |
| 8 | GRNN 广义回归神经网络分类 | 基于径向基函数回归 | 函数逼近、时间序列 |
| 9 | GRU 门控循环单元分类 | 门控机制简化 LSTM | 序列建模 |
| 10 | KELM 混合核极限学习机分类 | 结合多核 ELM | 高维复杂数据 |
| 11 | KNN 分类 | 基于距离的分类方法 | 模式识别 |
| 12 | LSSVM 最小二乘法支持向量机分类 | 最小二乘优化 SVM | 小样本分类 |
| 13 | LSTM 长短时记忆网络分类 | 门控机制处理长期依赖 | 语言建模 |
| 14 | MLP 全连接神经网络分类 | 多层感知机 | 通用分类 |
| 15 | PNN 概率神经网络分类 | 基于贝叶斯原理 | 模式识别 |
| 16 | RELM 鲁棒极限学习机分类 | 增强鲁棒性的 ELM | 噪声数据 |
| 17 | RF 随机森林分类 | 多棵决策树集成 | 高维、非线性数据 |
| 18 | SCN 随机配置网络模型分类 | 随机生成网络结构 | 快速训练 |
| 19 | SVM 支持向量机分类 | 寻找最优分类超平面 | 二分类、多分类 |
| 20 | XGBOOST 分类 | 梯度提升决策树 | 大规模结构化数据 |
| 21 | ANFIS 自适应模糊神经网络预测 | 融合模糊逻辑与神经网络 | 复杂非线性系统建模 |
| 22 | ANN 人工神经网络预测 | 多层神经元网络 | 通用预测任务 |
| 23 | ARMA 自回归滑动平均模型预测 | 线性时间序列建模 | 时间序列预测 |
| 24 | BF 粒子滤波预测 | 基于蒙特卡洛采样 | 动态系统状态估计 |
| 25 | BiLSTM 双向长短时记忆神经网络预测 | 双向捕获序列信息 | 时间序列、文本预测 |
| 26 | BLS 宽度学习神经网络预测 | 增量学习结构 | 在线学习 |
| 27 | BP 神经网络预测 | 误差反向传播训练 | 通用预测 |
| 28 | CNN 卷积神经网络预测 | 自动特征提取 | 图像、视频预测 |
| 29 | DBN 深度置信网络预测 | 多层无监督预训练 | 特征学习预测 |
| 30 | DELM 深度学习极限学习机预测 | 结合 ELM 与深度结构 | 复杂预测任务 |
| 31 | DKELM 回归预测 | 动态核 ELM 回归 | 时间序列回归 |
| 32 | ELMAN 递归神经网络预测 | 递归结构处理时序 | 时间序列 |
| 33 | ELM 极限学习机分类 | 随机生成隐藏层,快速训练 | 小样本学习 |
| 34 | GRNN 广义回归神经网络预测 | 基于径向基函数回归 | 函数逼近、时间序列 |
GMM 高斯混合模型预测: 多高斯分布建模,密度估计、聚类。
GRNN 广义回归神经网络预测: 径向基函数回归,函数逼近。
GRU 门控循环单元预测: 简化门控机制的 LSTM,时间序列预测。
KELM 混合核极限学习机预测: 多核 ELM 回归,高维回归。
LMS 最小均方算法预测: 线性回归的迭代优化,自适应滤波。
LSSVM 最小二乘法支持向量机预测: 最小二乘优化 SVM,回归预测。
LSTM 长短时记忆网络预测: 门控处理长期依赖,时间序列预测。
RBF 径向基函数神经网络预测: 径向基函数逼近,函数拟合。
RELM 鲁棒极限学习机预测: 增强鲁棒性的 ELM,噪声数据回归。
RF 随机森林预测: 决策树集成,回归预测。
RNN 循环神经网络预测: 循环连接处理序列,时间序列预测。
RVM 相关向量机预测: 稀疏贝叶斯学习,回归、分类。
SVM 支持向量机预测: 寻找最优超平面,回归预测。
TCN 时间卷积神经网络预测: 一维卷积处理时序,时间序列预测。
XGBoost 回归预测: 梯度提升决策树,大规模回归。

 扫码加好友,拉您进群
扫码加好友,拉您进群




 收藏
收藏

