
set.seed(123)
nn_double <- neuralnet(
Class ~ .,
data = Sonar_norm[train_index, ],
hidden = c(4, 4), # 双隐藏层结构
linear.output = FALSE,
act.fct = "logistic"
)
# 双层模型评估
prob_double <- predict(nn_double, Sonar_norm[-train_index, ])
pred_double <- ifelse(prob_double > 0.5, "R", "M")
pred_double <- factor(pred_double, levels = c("M", "R"))
# 使用confusionMatrix计算详细指标
test_conf_double <- confusionMatrix(pred_double, test_data$Class, positive = "M")
cat("\n双隐藏层模型 (4-4神经元) 性能:\n")
print(test_conf_double)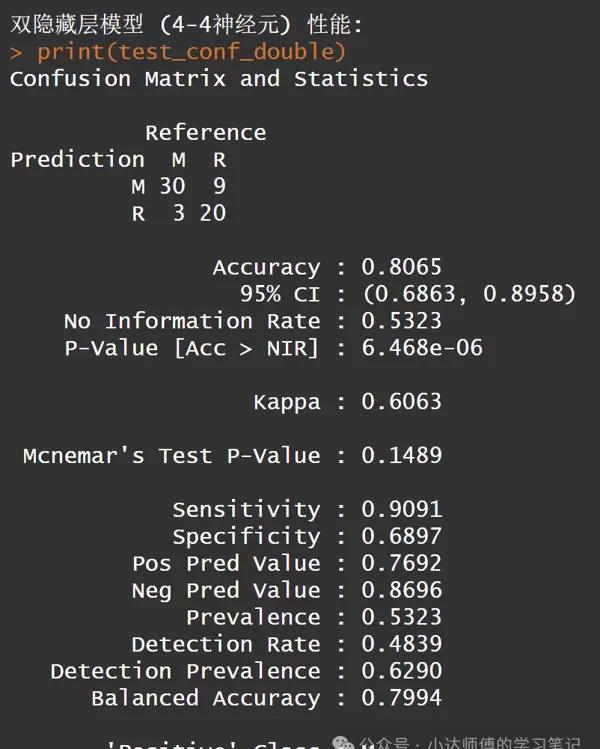
对比单隐藏层与双隐藏层的结果。可以看出,这个双隐藏层模型(4-4神经元)的准确性比上述单隐藏层模型(10神经元)更高。接下来,我们将继续探讨不同数量的双隐藏层神经元如何影响模型性能。
2.4参数调整确定最佳双隐藏层结构
这里仅简单展示参数配置过程,有兴趣的朋友可以自行尝试其他设置。
best_accuracy <- 0
best_config <- c(0, 0)
accuracy_matrix <- matrix(NA, nrow = 10, ncol = 10)
for(i in 1:10) {
for(j in 1:10) {
set.seed(123)
model <- neuralnet(
Class ~ .,
data = Sonar_norm[train_index, ],
hidden = c(i, j),
linear.output = FALSE,
act.fct = "logistic"
)
prob <- predict(model, Sonar_norm[-train_index, ])
pred <- ifelse(prob > 0.5, "R", "M")
pred <- factor(pred, levels = c("M", "R"))
# 使用confusionMatrix计算准确率
conf_matrix <- confusionMatrix(pred, test_data$Class, positive = "M")
current_accuracy <- conf_matrix$overall['Accuracy']
accuracy_matrix[i, j] <- current_accuracy
if(current_accuracy > best_accuracy) {
best_accuracy <- current_accuracy
best_config <- c(i, j)
}
}
}
# 输出最优参数
cat("\n===== 最优参数结果 =====\n")
cat("最佳隐藏层配置:", best_config[1], "-", best_config[2], "神经元\n")
cat("最高准确率:", best_accuracy, "\n")
print("准确率矩阵:")
print(accuracy_matrix)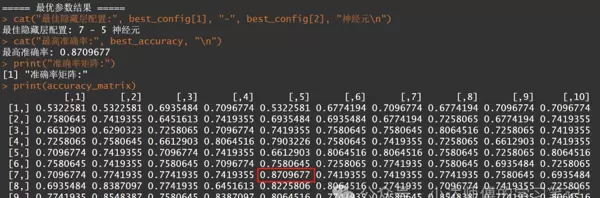
从上述结果可以看出,在这个10*10的矩阵中,7-5双层神经元的准确性最高。
2.5最终模型拟合与评估
接下来,我们将对7-5的双隐藏层模型进行评估并绘制其神经网络图。
set.seed(123)
final_nn <- neuralnet(
Class ~ .,
data = Sonar_norm[train_index, ],
hidden = best_config,
linear.output = FALSE,
act.fct = "logistic"
)
# 最终模型评估
prob_final <- predict(final_nn, Sonar_norm[-train_index, ])
pred_final <- ifelse(prob_final > 0.5, "R", "M")
pred_final <- factor(pred_final, levels = c("M", "R"))
# 使用confusionMatrix计算详细指标 (正类为"M")
test_conf_final <- confusionMatrix(pred_final, test_data$Class, positive = "M")
cat("\n最终模型性能:\n")
print(test_conf_final)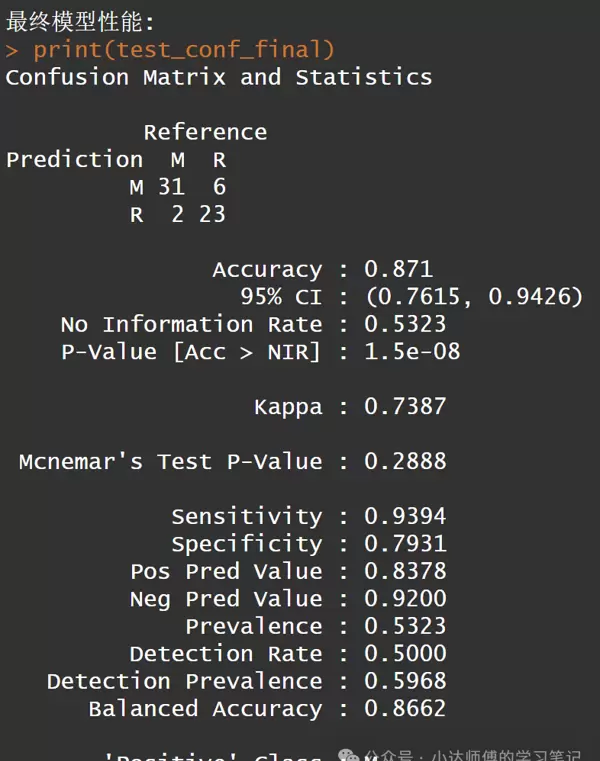
这是最佳模型的混淆矩阵结果。接下来,我们继续可视化神经网络:
plot(final_nn, rep = "best",
col.entry = "skyblue",
col.hidden = "lightgreen",
col.out = "salmon",
main = "最优神经网络结构")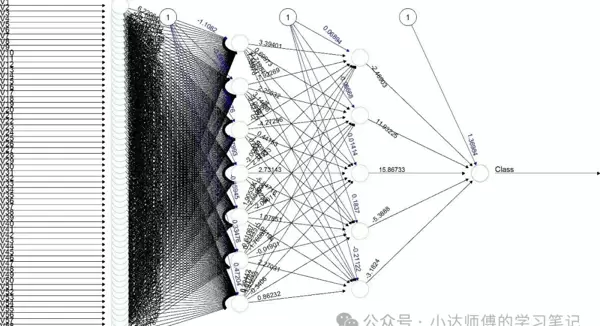
2.6与逻辑回归对比
最后,我们将简单地将该模型的预测结果与逻辑回归的预测效果进行比较:
logit_model <- glm(Class ~ .,
data = train_data,
family = binomial(link = "logit"))
prob_logit <- predict(logit_model, test_data, type = "response")
pred_logit <- ifelse(prob_logit > 0.5, "R", "M")
pred_logit <- factor(pred_logit, levels = c("M", "R"))
# 使用confusionMatrix计算详细指标
logit_conf <- confusionMatrix(pred_logit, test_data$Class, positive = "M")
cat("\n逻辑回归性能:\n")
print(logit_conf)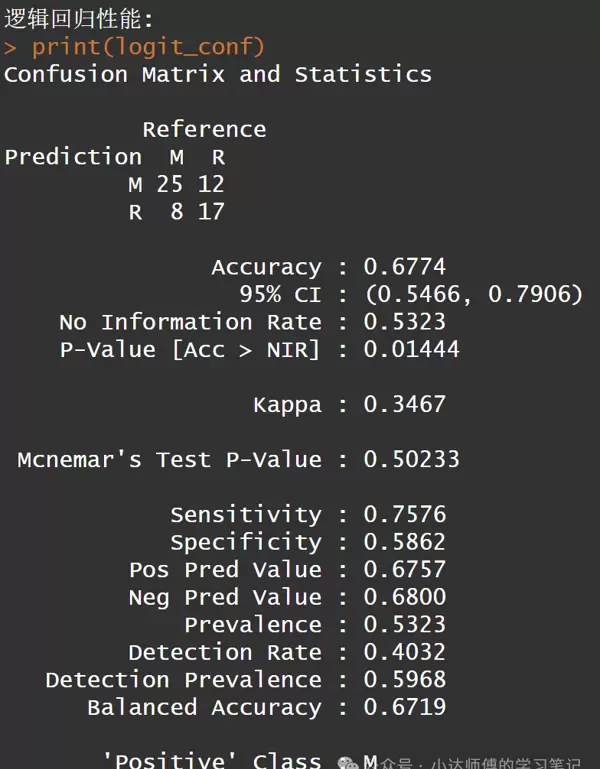
可以看出,神经网络模型的表现明显优于逻辑回归模型。
简要查看这两个模型的预测结果(受篇幅限制,仅展示前20个)。
# 模型预测结果
results <- data.frame(
Actual = test_data$Class,
NN_Probability = prob_final,
NN_Prediction = pred_final,
Logit_Probability = prob_logit,
Logit_Prediction = pred_logit
)
# 查看前20个样本的预测结果
print(head(results, 20))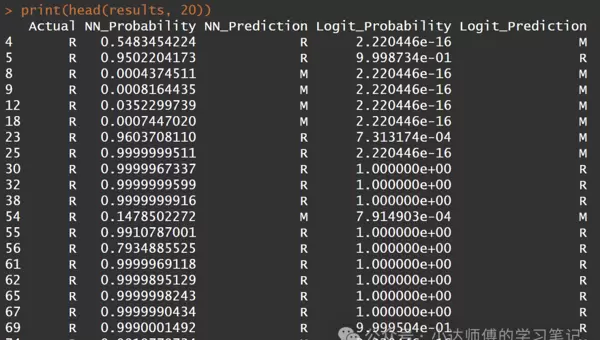
最后,绘制ROC曲线评估两个模型的表现。
roc_nn <- roc(response = test_data$Class, predictor = as.numeric(prob_final))
roc_logit <- roc(response = test_data$Class, predictor = prob_logit)
plot(roc_nn, col = "blue", main = "ROC曲线比较")
lines(roc_logit, col = "red")
legend("bottomright", legend = c(paste("神经网络 (AUC =", round(auc(roc_nn), 3)),
paste("逻辑回归 (AUC =", round(auc(roc_logit), 3))),
col = c("blue", "red"), lwd = 2)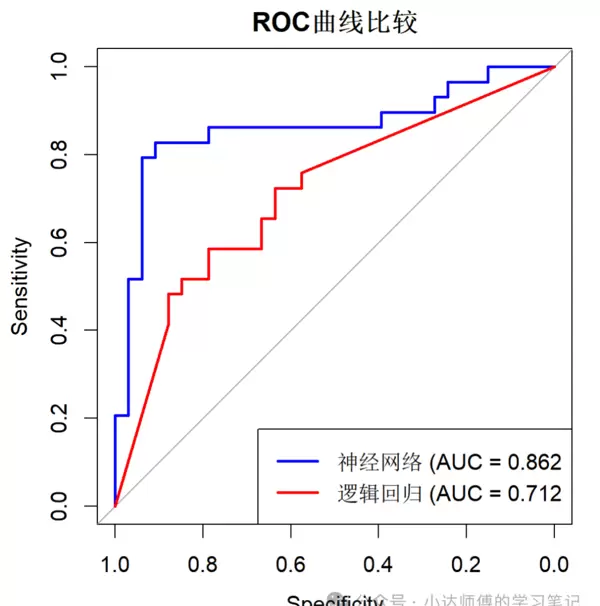
本次实践展示了神经网络在声呐数据分类中的应用,突显了其处理复杂模式识别任务时的优势。通过R语言的neuralnet包,我们迅速构建并优化了神经网络模型,最终达到了超越传统方法的分类效果。
如何学习大规模模型?
学习AI大型模型是一个系统化的过程,需要从基础知识开始,逐步深入到更高级的技术领域。
这里为大家仔细筛选了一份详尽的AI大模型学习资料,涵盖:从基础到实践的完整学习路径、精选的大模型学习书籍与手册、视频教程、实战练习以及面试题目等,这些资源均免费提供!这是一份适合零起点至进阶阶段的学习路线概览,建议大家收藏起来。

100个AI大模型商业化实施方案
大模型完整视频教程集锦

200册大模型PDF图书
????掌握后的成果:???? ? 基于大模型的全栈开发实现(包括前端、后端、产品经理、设计和数据分析等),学习本课程将有助于提升多种技能; ? 能够利用大模型解决实际项目中的需求:在大数据背景下,众多企业和机构面临大量数据处理的需求,使用大模型技术能够更高效地处理这些信息,增强数据分析与决策的精确度。因此,掌握大模型应用开发技巧,可以使开发者更好地满足真实项目的挑战; ? 基于企业级数据AI应用的开发,达成大模型理论的理解、掌握GPU运算能力、硬件知识以及LangChain开发框架和项目实战技能,学会垂直领域的细调训练(包括数据准备、数据提炼及大模型部署)一应俱全的学习; ? 能够完成当前热门的大模型特定领域模型训练任务,提高开发者的编程技巧:学习大模型应用开发涉及掌握机器学习算法、深度学习平台等技术,这些技能的获取可以增强开发者的编码与分析能力,使其能够更熟练地编写高质量代码。 LLM面试题目汇总

大模型产品经理资料集锦
大模型项目实战资源合辑
????有兴趣的朋友,可以通过扫描下方二维码免费获取【确保100%无费用】????
 扫码加好友,拉您进群
扫码加好友,拉您进群