决策树回归的内容

feierdeai08

收藏 2025-11-15

学习视频：https://www.bilibili.com/video/BV1owrpYKEtP?t=1.3&p=94

一、决策树回归的基本概念

决策树是一种非参数监督学习模型，既适用于分类任务（如决策树分类），也适用于回归任务（如决策树回归）。

在回归任务中，决策树的目标是通过对特征的逐层划分，将数据集分割成多个子集，每个子集最终生成一个预测值（通常是该子集中样本标签的平均值）。

与分类树不同，回归树的分裂标准不是“纯度”（如信息熵、基尼系数），而是“方差”——我们希望分裂后的子集中样本的方差尽可能小，以提高预测的稳定性。

二、决策树回归的最终预测结构

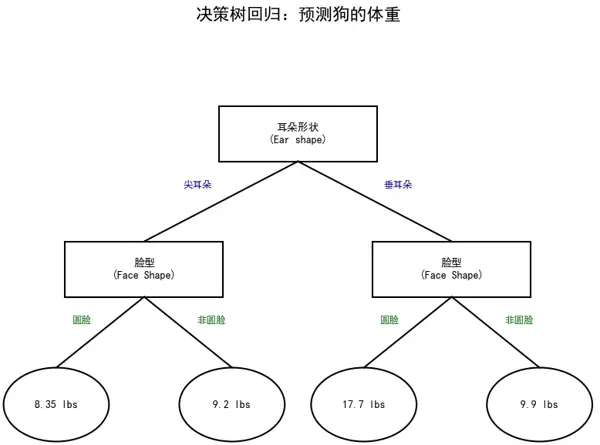
上图展示了一棵用于** 预测 “狗的体重（lbs.）”** 的回归决策树，其分裂逻辑和预测过程如下：

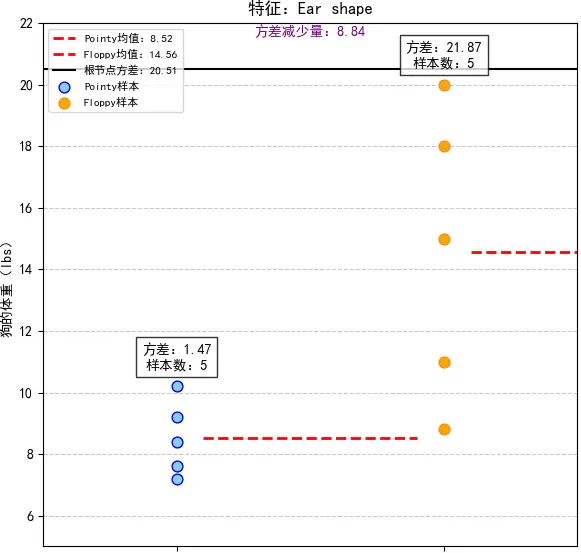
根节点分裂：Ear shape（耳朵形状）
- 分为两个分支：
  - ```
  Pointy（尖耳朵）
```
- ```
Floppy（垂耳朵）
```
二级节点分裂：Face Shape（脸型）
- 对于
```
Pointy
```
  分支，继续按
```
Face Shape
```
  分裂为
```
Round（圆脸）
```
  和
```
Not Round（非圆脸）
```
- 对于
```
Floppy
```
  分枝，同样按
```
Face Shape
```
  分裂为
```
Round
```
  和
```
Not Round
```
叶节点的预测值（均值）
- ```
Ear shape=Pointy + Face Shape=Round
```
  ：样本体重为
```
7.2, 8.4, 7.6, 10.2
```
  ，平均值为 (7.2+8.4+7.6+10.2)/4=8.35
- ```
Ear shape=Pointy + Face Shape=Not Round
```
  ：样本体重为
```
9.2
```
  ，平均值为 9.2
- ```
Ear shape=Floppy + Face Shape=Round
```
  ：样本体重为
```
15, 18, 20
```
  ，平均值为 (15+18+20)/3=17.7
- ```
Ear shape=Floppy + Face Shape=Not Round
```
  ：样本体重为
```
8.8, 11
```
  ，平均值为 (8.8+11)/2=9.9

三、分裂节点的选择（方差减少法）

决策树的核心问题是“如何选择最佳的分裂特征和分裂点”。通过“方差减少量”来量化不同特征的分裂效果，步骤如下：

根节点的初始方差（Variance at root node: 20.51）
- 首先计算所有样本体重的方差，作为根节点的初始方差。
- 假设所有样本的体重为：
```
7.2, 9.2, 8.4, 7.6, 10.2, 8.8, 15, 11, 18, 20
```
  （共 10 个样本），平均值 μ=(7.2+9.2+8.4+7.6+10.2+8.8+15+11+18+20)/10=11.64，方差为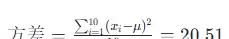
候选特征 1：Ear shape（耳朵形状）
- 分裂为
```
Pointy
```
  和
```
Floppy
```
  两个子集：
- ```
Pointy
```
  子集：5 个样本，体重
```
7.2, 9.2, 8.4, 7.6, 10.2
```
  ，平均值 μ1=8.52，方差为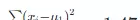
- ```
Floppy
```
  子集：5 个样本，体重
```
8.8, 15, 11, 18, 20
```
  ，平均值 μ2=14.56，方差为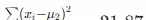
- 方差减少量的计算公式为：
  - 方差减少量 = 根节点方差 - (wleft × 左子集方差 + wright × 右子集方差)
  - 其中，wleft 和 wright 分别是左右子集的样本比例（此处均为 5/10）。代入得：20.51 - (5/10 × 1.47 + 5/10 × 21.87) = 8.84
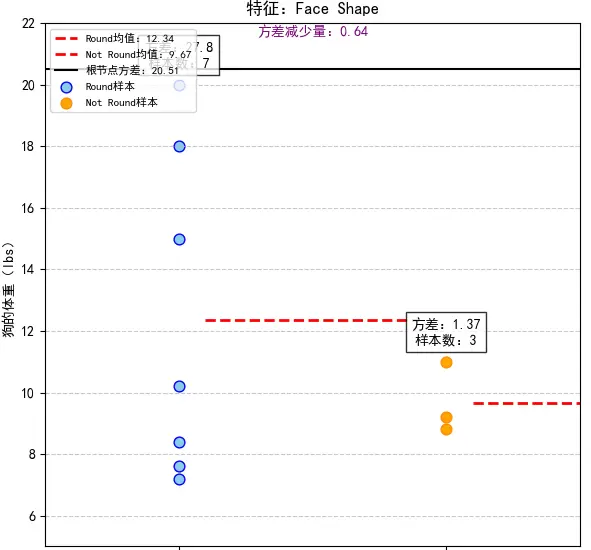
候选特征 2：Face Shape（脸型）
- 分裂为
```
Round
```
  和
```
Not Round
```
  两个子集：
- ```
Round
```
  子集：7 个样本，体重
```
7.2, 15, 8.4, 7.6, 10.2, 18, 20
```
  ，平均值 μ1 ≈ 12.34，方差为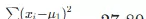
- ```
Not Round
```
  子集：3 个样本，体重
```
9.2, 8.8, 11
```
  ，平均值 μ2 ≈ 9.67，方差为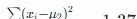
- 样本比例 wleft = 7/10，wright = 3/10，代入方差减少量公式：20.51 - (7/10 × 27.80 + 3/10 × 1.37) = 0.64
候选特征 3：Whiskers（胡须）
- 分裂为
```
Present
```
  和
```
Absent
```
  两个子集：
- ```
Present
```
  子集：4 个样本，体重
```
7.2, 8.8, 9.2, 8.4
```
  ，平均值 μ1 = 8.4，方差为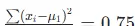
- ```
Absent
```
  子集：6 个样本，体重
```
15, 7.6, 11, 10.2, 18, 20
```
  ，平均值 μ2 ≈ 13.63，方差为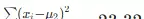
- 样本比例 wleft = 4/10，wright = 6/10，代入方差减少量公式：20.51 - (4/10 × 0.75 + 6/10 × 23.32) = 6.22
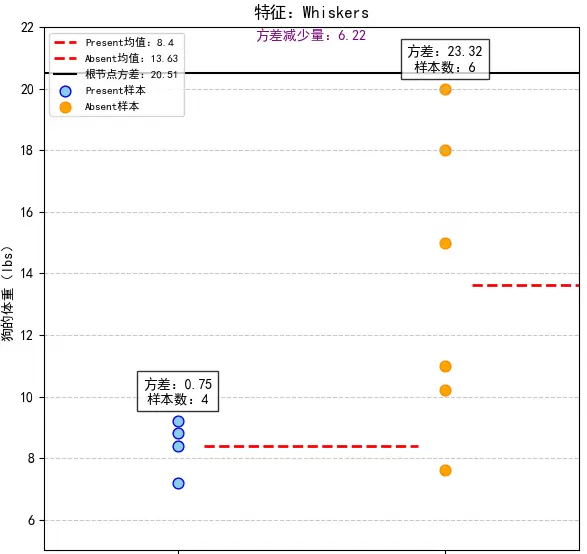
选择最佳分裂特征
- 对比三个特征的方差减少量：
```
Ear shape（8.84）> Whiskers（6.22）> Face Shape（0.64）
```
  。
- 因此，选择 “Ear shape” 作为根节点的分裂特征，因为它能最大程度地减少方差，分裂效果最佳。