基于Sobol的全局参数灵敏度分析

可自行更改参数数量和目标函数 MATLAB编程

在工程优化、计算机仿真和数据解析等领域，参数灵敏度分析是一项关键的技术。它有助于我们理解哪些参数对目标函数影响最大，从而指导我们合理分配资源和优化模型。在多种参数灵敏度分析方法中，Sobol方法因其卓越的全局分析能力而备受关注。

方法简介

Sobol方法是一种基于方差分解的全局灵敏度分析方法，通过评估每个参数对目标函数变化的贡献率，来衡量参数的重要性。与局部方法不同，Sobol方法可以同时考虑参数的主要效果和交互效果，适合高维度问题。

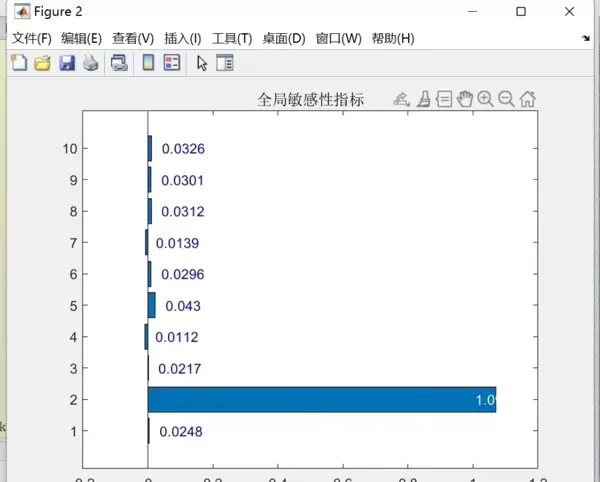
Sobol方法的核心理念是将输入参数分解成多个独立的随机变量，并通过构建伪蒙特卡罗序列来估算每个变量对输出的贡献。具体而言，Sobol方法通过计算每个参数的Sobol指数（亦称重要性指标），来评估其对目标函数的贡献程度。

Matlab实现

为了展示Sobol方法的实现，我们以以下简单的目标函数为例：

function y = target_function(x)
    y = x1 + 2*x2 + 3*x3 + 4*x4;
end

在这个目标函数中，我们有4个输入参数x1至x4。目标函数是线性的，每个参数的系数决定了其对目标函数的贡献。

接下来，我们使用Matlab实现Sobol方法。以下是实现步骤：

• 安装所需的工具箱或下载相关的Matlab代码。
• 生成Sobol序列。Sobol序列是一种伪蒙特卡罗序列，能够均匀地覆盖输入空间。
• 计算每个参数的Sobol指数。
• 绘制结果，分析参数的重要性。

以下是具体的Matlab代码实现：

% 定义目标函数
function y = target_function(x)
    y = x1 + 2*x2 + 3*x3 + 4*x4;
end

% 定义参数数目
n_params = 4;

% 生成Sobol序列
n_samples = 1000;
sobol = sobolset(n_params, 'NumPoints', n_samples);

% 计算Sobol指数
sobol_indices = sobolensitivity(sobol, @target_function);

% 绘制结果
bar(sobol_indices);
title('Sobol Indices');
xlabel('Parameters');
ylabel('Importance');

代码解释：

sobolset

此函数用于生成Sobol序列。

sobolensitivity

此函数用于计算Sobol指数。

bar

此函数用于绘制条形图，直观展示每个参数的重要性。

运行上述代码后，会得到一个条形图，显示每个参数的Sobol指数。在本例中，由于目标函数是线性的，参数x4的Sobol指数最高，其次是x3，x2，最后是x1。

代码分析

在上述代码中，我们首先定义了一个目标函数

target_function

，它接收一个输入向量

x

，并返回一个标量输出

y

。这个目标函数是线性的，每个参数的系数决定了其对输出的贡献。

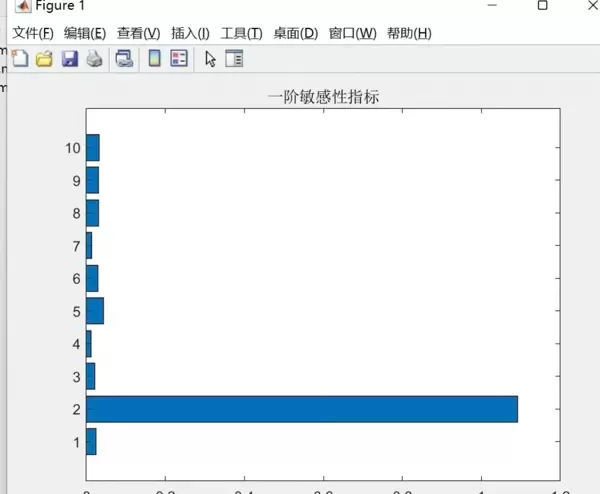
接下来，我们生成了一个Sobol序列，包含4个参数，每个参数的样本数为1000。Sobol序列是一种伪蒙特卡罗序列，能够均匀地覆盖输入空间，从而确保估计的准确性。

然后，我们调用

sobolensitivity

函数，计算每个参数的Sobol指数。Sobol指数是一个介于0和1的值，表示该参数对目标函数变化的贡献率。Sobol指数越接近1，表示该参数对目标函数的影响越大。

最后，我们使用

bar

函数绘制条形图，直观展示每个参数的Sobol指数。条形图的高度表示参数的重要性，颜色表示参数的索引。

通过这个简单的示例，我们可以看到Sobol方法在参数灵敏度分析中的应用。即使在高维度问题中，Sobol方法也能有效评估参数的重要性。

结论

Sobol方法是一种强大的全局参数灵敏度分析工具，能够同时考虑参数的主要效果和交互效果。通过Matlab代码的实现，我们可以轻松地应用Sobol方法来分析复杂的系统和模型。在实际应用中，可以根据具体需求调整参数数量和目标函数，从而实现个性化的分析需求。