当圆柱锂电池遇上多物理场：COMSOL如何玩转热分布与复杂耦合

锂电池的热管理是一项技术挑战。试想一下，几十节圆柱电芯堆叠在一起，如果某个区域的温度失控，轻则缩短电池寿命，重则引发安全事故。在这种情况下，COMSOL的多物理场耦合能力显得尤为重要——它可以实现热-流-固四场联动，甚至能够精确模拟孔隙率的动态变化。

热分布：从产热方程到散热设计

锂电池发热的主要原因是电化学反应的产热速率。在COMSOL中，可以通过PDE模块自定义产热模型。例如，一个简化的产热公式如下：

// 产热速率（W/m?）
Q = I^2 * R + entropy_coeff * I * (T - T_ref);
// 热传导方程
pde(ht, T, 'T') = div(k*grad(T)) + Q;

其中，

I

R

entropy_coeff

div(k*grad(T))

Q

然而，电芯之间还存在冷却风道，气流和温度场相互影响。这时需要使用流固耦合（FSI）。例如，可以通过“非等温流”接口耦合流体传热和固体导热，再利用“固体力学”接口计算电芯膨胀对风道截面积的影响。

孔隙率会动？动态渗透率的骚操作

在瓦斯抽采等场景中，煤层的渗透率不是一个固定值，它会随孔隙率和应力的变化而变化。COMSOL的PDE模块加上固体力学接口可以构建一个动态模型：

// 孔隙率随体积应变变化
phi = phi0 - alpha * epsilon_vol;  
// 动态渗透率公式（经验模型）
k = k0 * pow(phi/phi0, 3) * pow(sigma/sigma0, -beta);  
// 瓦斯流动方程（达西定律）
pde(fp, p) = div((k/mu)*grad(p)) - S;

在这段代码中，

sigma

beta

k

phi

四场耦合实战：热-流-固-化反一起上

锂电池热失控仿真的复杂性在于需要同时考虑多个物理场，例如：

• 电化学场：锂离子浓度分布
• 传热场：温度传导
• 流体场：冷却液流动
• 固体力学场：电芯膨胀挤压

此时可以使用多物理场接口进行“拼积木”式的建模。例如，使用“二次电流分布”接口进行电化学建模，使用“非等温流”接口耦合流体和传热，再通过“热膨胀”节点将温度场映射到固体变形。

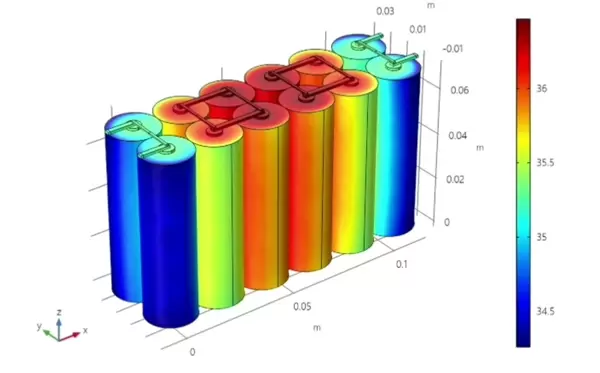
以下是一个实际参数设置的例子：

// 电芯膨胀应变（温度+锂浓度驱动）
epsilon = alpha_T*(T-T0) + alpha_c*(c-c0);  
// 固体力学边界条件：固定电池底部
solid.fix('u') = 0; // 底部位移归零

其中，alpha T 是热膨胀系数，

alpha

c

T

c

电磁热耦合：另一个隐藏副本

你以为这就结束了？电磁热耦合同样能带来精彩的应用。例如，在无线充电场景下，金属部件中的涡流发热问题：

// 电磁损耗密度（焦耳热）
Q_eddy = sigma_elec * normE^2;  
// 传热方程直接调用电磁场计算的Q_eddy
pde(ht, T, 'T') = div(k*grad(T)) + Q_eddy;

其中，

normE

Q_eddy

最后说点人话

多物理场仿真就像烹饪一道复杂的菜肴——选择合适的“食材”（物理场）并控制好“火候”（耦合方式）。COMSOL的优势在于可以自由组合各种“食材”，PDE模块就像一个万能锅，可以根据需要添加不同的材料。当然，如果时间紧迫或任务繁重，寻找专业的代做服务来复现实验数据也是一个合理的选择。有需求的同学，欢迎在评论区交流（手动狗头）。