Matlab与Vensim PLE在演化博弈建模中的应用

在博弈论研究中，多主体演化博弈模型一直是既有趣又具挑战性的领域。本文将探讨Matlab在两方、三方乃至四方演化博弈建模的应用，以及Vensim PLE在系统动力学模型中的独特优势。

Matlab：演化博弈建模与分析的好帮手

建模与方程求解

首先，让我们来看看Matlab在多方演化博弈建模方面的应用。以两方演化博弈为例，假设有两个策略A和B，其收益矩阵如下所示：

\[ R = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \]

其中，a, b, c, d分别代表不同策略组合下的收益。在Matlab中，我们可以这样定义收益矩阵：

R = [a, b; c, d];

接下来，根据演化博弈理论，我们需要建立复制者动态方程。对于策略A的频率 \( x \)，其动态方程为：

\[ \dot{x} = x(1 - x)[x(a - c) + (1 - x)(b - d)] \]

在Matlab中，我们可以通过定义函数来表示这个方程：

function dxdt = replicator_dynamics(t, x, R)
    a = R(1, 1); b = R(1, 2); c = R(2, 1); d = R(2, 2);
    dxdt = x * (1 - x) * (x * (a - c) + (1 - x) * (b - d));
end

之后，我们可以使用Matlab的数值求解器，例如：

ode45

来求解这个微分方程：

tspan = [0 100]; % 时间范围
x0 = 0.5; % 初始条件
[~, x] = ode45(@(t, x) replicator_dynamics(t, x, R), tspan, x0);

这里，

ode45

函数将在

tspan

时间范围内，从初始条件

x0

开始求解我们定义的微分方程

replicator_dynamics

。

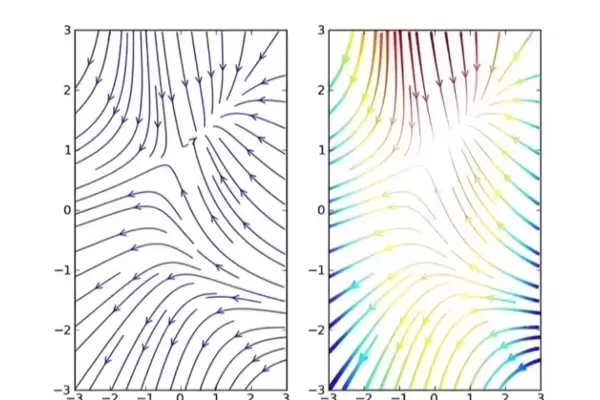
相位图与稳定性分析

求解完方程后，我们可以通过相位图和稳定性分析进一步理解系统的行为。相位图能够直观展示系统在不同状态下的演化趋势。以两方博弈为例，绘制相位图的代码如下：

x = linspace(0, 1, 100);
dxdt = zeros(size(x));
for i = 1:length(x)
    dxdt(i) = replicator_dynamics(0, x(i), R);
end

figure;
plot(x, dxdt);
xlabel('Frequency of Strategy A (x)');
ylabel('dx/dt');
title('Phase Diagram of Two - player Evolutionary Game');

通过观察相位图，我们可以识别出系统在哪些点是稳定的，哪些点是不稳定的。为了更深入地分析稳定性，我们还需要利用雅克比矩阵。对于两方博弈，雅克比矩阵是方程对 \( x \) 的导数：

\[ J = \frac{\partial \dot{x}}{\partial x} = (1 - 2x)[x(a - c) + (1 - x)(b - d)] + x(1 - x)(a - c - b + d) \]

在Matlab中，我们可以定义一个函数来计算雅克比矩阵：

function J = jacobian(x, R)
    a = R(1, 1); b = R(1, 2); c = R(2, 1); d = R(2, 2);
    J = (1 - 2 * x) * (x * (a - c) + (1 - x) * (b - d)) + x * (1 - x) * (a - c - b + d);
end

通过分析雅克比矩阵在平衡点处的特征值，我们可以判断平衡点的稳定性。如果特征值的实部小于0，则该平衡点是局部渐近稳定的。

Matlab数值仿真模拟

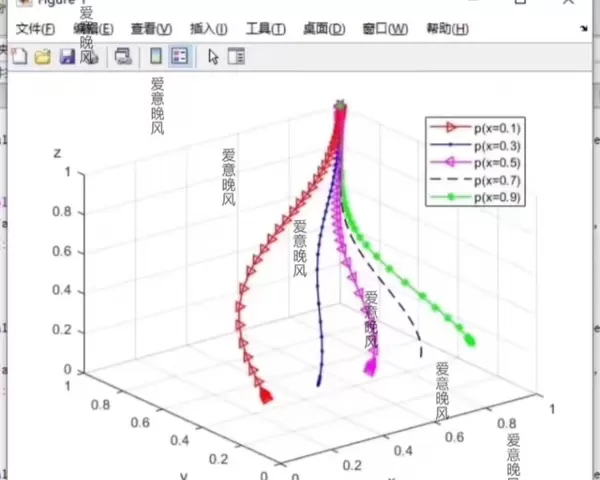
数值仿真模拟是Matlab的一大强项。我们可以通过给参数赋值，观察不同初始条件下的演化路径。例如，改变初始策略A的频率，观察系统的演化情况：

x0_values = [0.1, 0.3, 0.7, 0.9];
figure;
hold on;
for i = 1:length(x0_values)
    x0 = x0_values(i);
    [t, x] = ode45(@(t, x) replicator_dynamics(t, x, R), tspan, x0);
    plot(t, x);
end
xlabel('Time');
ylabel('Frequency of Strategy A (x)');
title('Evolution Paths with Different Initial Conditions');
hold off;

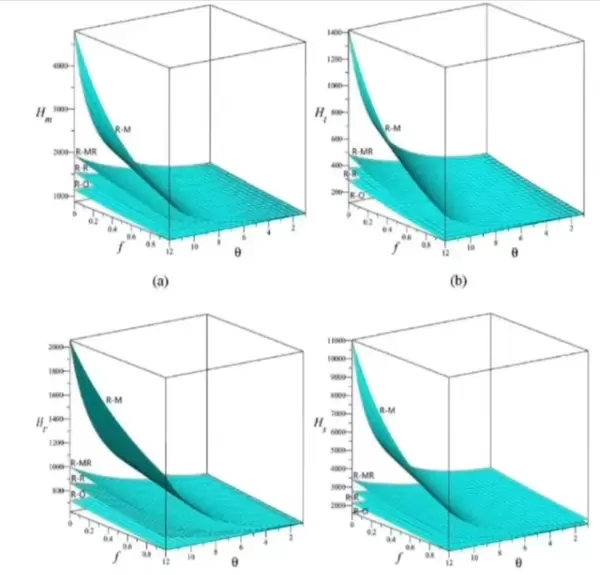
此外，我们还可以进行参数敏感性分析。例如，改变收益矩阵 \( R \) 中的某个元素，观察系统演化的变化：

R1 = [2, 1; 0, 3];
R2 = [2.5, 1; 0, 3];

x0 = 0.5;
[t1, x1] = ode45(@(t, x) replicator_dynamics(t, x, R1), tspan, x0);
[t2, x2] = ode45(@(t, x) replicator_dynamics(t, x, R2), tspan, x0);

figure;
plot(t1, x1, 'b', 'DisplayName', 'R1');
hold on;
plot(t2, x2, 'r', 'DisplayName', 'R2');
xlabel('Time');
ylabel('Frequency of Strategy A (x)');
title('Parameter Sensitivity Analysis');
legend;
hold off;

含有动态奖惩机制的演化系统稳定性控制

动态奖惩机制是控制演化系统稳定性的重要手段，它可以分为线性动态奖惩和非线性动态奖惩。

假设线性动态奖惩函数如下：

\[ \Delta p = k (x - x^*) \]

其中 \( k \) 是奖惩系数，\( x^* \) 是目标频率。在Matlab中，我们可以将这种奖惩机制加入到之前的复制者动态方程中：

function dxdt = replicator_dynamics_with_linear_reward(t, x, R, k, x_star)
    a = R(1, 1); b = R(1, 2); c = R(2, 1); d = R(2, 2);
    dxdt = x * (1 - x) * (x * (a - c) + (1 - x) * (b - d)) + k * (x - x_star);
end

非线性动态奖惩可能更为复杂，例如：

\[ \Delta p = k (x - x^*)^2 \]

相应的Matlab函数为：

function dxdt = replicator_dynamics_with_nonlinear_reward(t, x, R, k, x_star)
    a = R(1, 1); b = R(1, 2); c = R(2, 1); d = R(2, 2);
    dxdt = x * (1 - x) * (x * (a - c) + (1 - x) * (b - d)) + k * (x - x_star)^2;
end

通过调整奖惩系数 \( k \) 和目标频率 \( x^* \)，我们可以有效控制演化系统的稳定性。

Vensim PLE：系统动力学模型的演化博弈仿真

因果逻辑关系与流量存量图

Vensim PLE在系统动力学模型的演化博弈仿真中具有独特优势。首先，我们需要梳理因果逻辑关系。例如，在一个简单的市场竞争演化博弈中，企业的市场份额会影响其收益，收益又会影响其策略调整，而策略调整又会反过来影响市场份额。

在Vensim PLE中，我们通过绘制流量存量图来直观表示这些关系。流量表示随时间变化的速率，存量则是积累的状态。例如，“市场份额”可以是一个存量，“策略调整速率”可以是一个流量。

模型调试

绘制好流量存量图后，就进入了模型调试阶段。在Vensim PLE中，我们可以通过设置各种参数，观察模型的输出是否符合预期。例如，给企业的收益函数设置不同的参数，观察市场份额的演化情况。如果发现模型输出不合理，我们需要检查因果逻辑关系和参数设置，逐步调试模型，直至其能准确反映我们想要模拟的演化博弈过程。

综上所述，Matlab与Vensim PLE在进化博弈的研究领域各有优势。合理利用这两种工具，可以帮助我们更深入地洞察并解析复杂的博弈体系。期望本文能够为相关领域的研究者提供一定的启示。