一、题目与代码及实验结果

题目展示如下：

对应的程序代码为：

clc ;clear all;close all;
%G1(S)
 num1=[1];
 temp1=[1,0];
 temp2=[1 2 2];
 temp3=[1 6 13];
 temp=conv(temp1,temp2);
 den1=conv(temp,temp3);
 figure;
 rlocus(num1,den1); grid
 title('G1(s)的根轨迹');
  G=tf(num1,den1);
  [k,r]=rlocfind(G);%或者[k,r]=rlocfind(num1,den1);
 %G1(s)的单位负反馈的阶跃响应
 figure
G1_c=feedback(G,1);
step(G1_c);grid
xlabel('t/s');
ylabel('G1_c(t)')
title('G1(s)的单位负反馈的阶跃响应');


%G2(S)
 num1=[1,12];
 temp1=[1,1];
 temp2=[1 12 100];
 temp3=[1 10];
 temp=conv(temp1,temp2);
 den1=conv(temp,temp3);
 figure;
 rlocus(num1,den1); grid
 title('G2(s)的根轨迹');
  G=tf(num1,den1);
 [k,r]=rlocfind(G);%或者[k,r]=rlocfind(num1,den1);
 %G2(s)的单位负反馈的阶跃响应
 figure
G2_c=feedback(G,1);
step(G2_c);grid
xlabel('t/s');
ylabel('G2_c(t)')
title('G2(s)的单位负反馈的阶跃响应');


%G3(S)
 num1=[0.05,1];
 temp1=[1,0];
 temp2=[0.0714 1];
 temp3=[0.012 0.1 1];
 temp=conv(temp1,temp2);
 den1=conv(temp,temp3);
 figure;
 rlocus(num1,den1); grid
 title('G3(s)的根轨迹');
  G=tf(num1,den1);
 [k,r]=rlocfind(G);%或者[k,r]=rlocfind(num1,den1);
 %G3(s)的单位负反馈的阶跃响应
 figure
G3_c=feedback(G,1);
step(G3_c);grid
xlabel('t/s');
ylabel('G3_c(t)')
title('G3(s)的单位负反馈的阶跃响应');

实验运行后得到的结果图像包括：

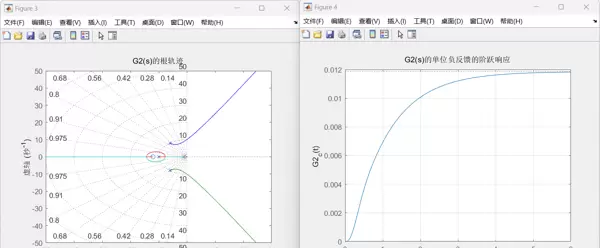
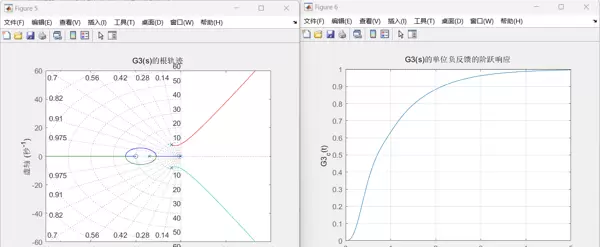
二、核心函数解析

1. 系统清理与初始化操作

clc; clear all; close all;

• clc：用于清空 MATLAB 命令窗口，提升界面整洁度。
• clear all：清除工作空间中的所有变量，防止历史数据对当前计算造成干扰。
• close all：关闭所有已打开的图形窗口，避免图表重叠显示。

上述命令构成了 MATLAB 脚本常见的起始三部曲，确保每次运行都在一个干净、独立的环境中进行。

2. 传递函数建模方法

tf(num, den)

功能说明：构建线性时不变（LTI）系统的传递函数模型。

调用方式：

G = tf(num, den)

num

—— 表示分子多项式系数向量，按 s 的降幂顺序排列。

den

—— 表示分母多项式系数向量，同样按照降幂排列。

实例说明：在定义 G(s) 时，使用了如下语句：

num1 = [1];
den1 = [1 8 25 26 26];
G = tf(num1, den1);

该行代码成功构建了指定形式的传递函数模型。

3. 根轨迹绘图函数详解

rlocus(G)

或

rlocus(num, den)

功能描述：用于计算并绘制系统根轨迹。根轨迹反映了当开环增益 K 从零逐渐增至无穷大时，闭环系统特征方程根在复平面（s 平面）上的运动路径。

使用格式：

rlocus(G)

—— 直接传入传递函数对象 G。

rlocus(num, den)

—— 使用分子和分母系数分别输入。

输出内容：生成一张包含以下元素的根轨迹图：

• 蓝色“×”标记代表开环极点（Open-loop Poles）。
• 红色“○”表示开环零点（Open-loop Zeros）。
• 黑色曲线即为根轨迹本身。

应用示例：

rlocus(num1, den1);

此命令将绘制出 G(s) 对应的完整根轨迹图。

4. 反馈系统连接函数

feedback(G, H)

功能说明：实现两个子系统 G 和 H 的反馈连接，默认采用负反馈结构。

语法结构：

closed_loop_G = feedback(G, H)

G

—— 前向通道的传递函数。

H

—— 反馈通道的传递函数。

内部计算逻辑：闭环传递函数由公式自动推导得出。

具体例子：

G1_c = feedback(G, 1);

其中

H = 1

表明系统采用单位负反馈配置。

5. 阶跃响应仿真工具

step(G)

功能作用：计算并可视化系统在单位阶跃输入信号下的时间响应曲线。

调用方式：

step(G)

G

—— 通常为闭环系统的传递函数模型。

输出图形信息：

• 横轴表示时间变量

t

• 纵轴表示系统输出响应值

y(t)

实际调用示例：

step(G1_c);

该指令会自动仿真并绘制出闭环系统 G_c(s) 的单位阶跃响应曲线。

6. 图形美化相关命令

figure

—— 开启一个新的绘图窗口，便于多图并列展示。

grid

—— 在当前图像中添加网格线，增强数据可读性。

title('文本')

—— 为图表设置标题文字。

xlabel('文本')

—— 给 x 轴添加标注说明。

ylabel('文本')

—— 给 y 轴添加标签说明。

三、程序结构剖析

整体代码设计条理清晰，遵循统一的分析流程，依次对三个不同系统（G, G, G）执行相同的操作序列：

针对每一个系统，均执行以下四个主要步骤：

1. 建立传递函数模型
   • 设定分子

   num1

   • 与分母

   den1

   • 的系数向量。
   • 其中分母通过

   conv

   • 函数实现多项式相乘，适用于多个因式相乘的情形。
   • 例如：

   den1 = conv(conv(temp1, temp2), temp3);

   • 等价于展开后的多项式表达式

   den1 = temp1 * temp2 * temp3

2. 绘制根轨迹图
   • 利用

   figure

   • 开启新图形窗口。
   • 调用

   rlocus

   • 绘制根轨迹曲线。
   • 结合

   grid

   • 和

   title

   • 等指令优化图表外观。
3. 构建闭环系统
   • 使用

   tf

   • 将系数封装为传递函数对象

   G

   • 再通过

   feedback(G, 1)

   • 形成单位负反馈下的闭环系统

   G_c

4. 仿真阶跃响应
   • 再次使用

   figure

   • 创建独立绘图区域。
   • 调用

   step

   • 进行阶跃响应仿真并绘图。
   • 配合

   grid

   • 、

   title

   • 、

   xlabel

   • 、

   ylabel

   • 等命令完善图像标注。

总结

• 根轨迹图绘制：用于研究开环增益 K 从 0 到 ∞ 变化过程中，闭环极点在 s 平面上的移动轨迹，辅助判断系统稳定性变化趋势。
• 阶跃响应曲线绘制：在单位负反馈架构下，施加单位阶跃输入，观察系统输出随时间演化的动态行为。
• 建模过程：

tf

• 分析手段：

rlocus

（用于评估系统稳定性）、

step

（用于分析瞬态性能指标）
• 系统连接方式：

feedback