

本文将帮助你深入理解卷积神经网络(CNN)的基本原理,并探讨其在计算机视觉任务中表现优异的原因。我们将以一个简单的实例作为切入点:使用卷积神经网络对MNIST手写数字数据集进行分类。此前在第2章中,我们曾使用全连接密集网络完成该任务,测试准确率约为97.8%。而接下来要介绍的卷积神经网络虽然结构简单,但性能将超越之前的模型。
代码清单8-1 展示了一个典型的卷积神经网络构建过程。它由多个 Conv2D 层与 MaxPooling2D 层交替堆叠而成,后续会详细解释这些层的功能。本例采用第7章介绍过的函数式API来搭建整个模型结构。
from tensorflow import keras from tensorflow.keras import layers inputs = keras.Input(shape=(28, 28, 1)) x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(inputs) x = layers.MaxPooling2D(pool_size=2)(x) x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x) x = layers.MaxPooling2D(pool_size=2)(x) x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x) x = layers.Flatten()(x) outputs = layers.Dense(10, activation="softmax")(x) model = keras.Model(inputs=inputs, outputs=outputs)
需要注意的是,卷积神经网络所接收的输入张量维度格式为 (image_height, image_width, image_channels)(不包含批量维度)。在此示例中,模型输入设定为 (28, 28, 1),恰好对应MNIST图像的标准尺寸和单通道灰度图特性。
通过代码清单8-2 可以输出该卷积神经网络的整体架构信息,便于我们了解各层的输出形状变化情况。
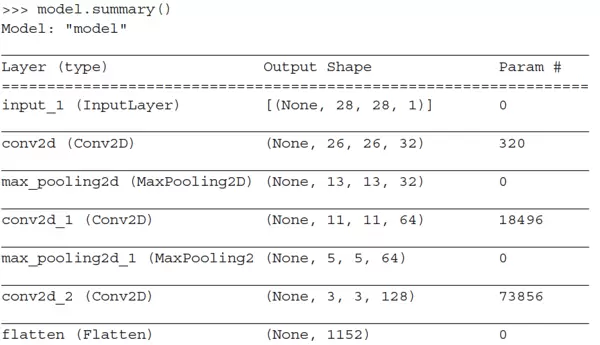

从上述模型结构可以看出,每个 Conv2D 层和 MaxPooling2D 层的输出均为三维张量,形状为 (height, width, channels)。随着网络层数加深,特征图的高度和宽度通常逐步减小,而通道数则由 Conv2D 层的第一个参数决定——如本例中的32、64 和 128。
最后一个卷积层输出的特征图尺寸为 (3, 3, 128),即一个128通道的3×3空间特征表示。为了将其送入后续的全连接分类器(即Dense层堆叠),必须先将三维特征展平为一维向量。因此,我们引入了 Flatten 层完成这一转换操作,之后再连接 Dense 层进行最终分类。
由于这是一个十类别的分类任务,网络最后一层使用了包含10个输出单元的全连接层,并配合 softmax 激活函数,以输出每个类别的概率分布。
接下来,我们在MNIST数据集上对该卷积神经网络进行训练。大部分预处理代码沿用自第2章的实现方式。考虑到当前任务是具有softmax输出的多类别分类问题,我们选用稀疏分类交叉熵损失函数(sparse_categorical_crossentropy),因为标签是以整数形式给出的。具体实现见代码清单8-3。
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype("float32") / 255
model.compile(
optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"]
)
model.fit(train_images, train_labels, epochs=5, batch_size=64)
我们在测试数据集上对模型进行了评估,代码如清单8-4所示。该代码展示了如何使用训练好的卷积神经网络进行性能测试。
>>> test_loss, test_acc = model.evaluate(test_images, test_labels)
>>> print(f"Test accuracy: {test_acc:.3f}")
Test accuracy: 0.991
 这种设计带来了两个关键优势:
这种设计带来了两个关键优势:
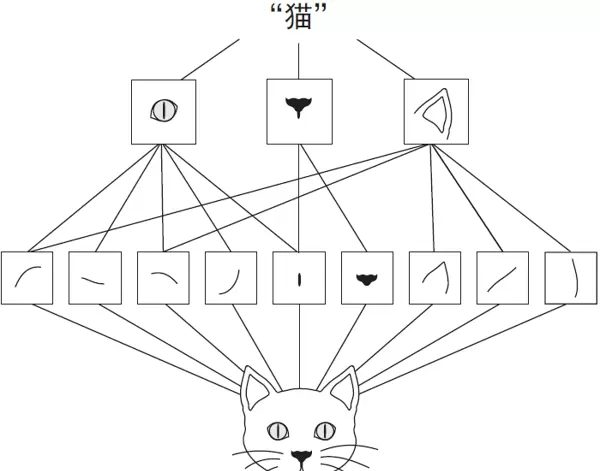 在MNIST示例中,第一个卷积层接收大小为(28, 28, 1)的输入特征图,并输出大小为(26, 26, 32)的特征图,意味着它应用了32个不同的滤波器。每个输出通道都是一个26×26的二维网格,记录了相应滤波器在整个输入图像上的激活情况,也被称为响应图(response map),如图8-3所示。
在MNIST示例中,第一个卷积层接收大小为(28, 28, 1)的输入特征图,并输出大小为(26, 26, 32)的特征图,意味着它应用了32个不同的滤波器。每个输出通道都是一个26×26的二维网格,记录了相应滤波器在整个输入图像上的激活情况,也被称为响应图(response map),如图8-3所示。
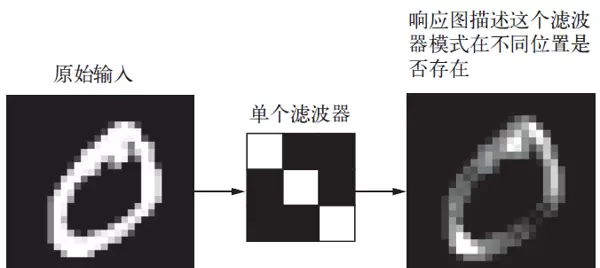 因此,“特征图”这一术语的含义是:在深度轴上的每一维都代表一个独立的特征检测器(即滤波器),而二维切片output[:, :, n]则表示该滤波器在输入空间各位置的响应强度分布。
因此,“特征图”这一术语的含义是:在深度轴上的每一维都代表一个独立的特征检测器(即滤波器),而二维切片output[:, :, n]则表示该滤波器在输入空间各位置的响应强度分布。
Conv2D(output_depth, (window_height, window_width)),其中前两个参数即为上述关键设置。
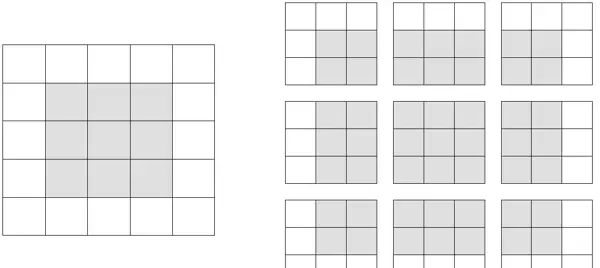 为了使输出特征图的空间尺寸与输入保持一致,通常采用填充(padding)技术。填充是指在输入特征图的四周添加额外的行和列,从而确保每个原始输入元素都能成为卷积窗口的中心。比如,使用3×3的卷积核时,需在上下各补1行、左右各补1列;而使用5×5的卷积核时,则需要补2行和2列,具体可参考图8-6。
为了使输出特征图的空间尺寸与输入保持一致,通常采用填充(padding)技术。填充是指在输入特征图的四周添加额外的行和列,从而确保每个原始输入元素都能成为卷积窗口的中心。比如,使用3×3的卷积核时,需在上下各补1行、左右各补1列;而使用5×5的卷积核时,则需要补2行和2列,具体可参考图8-6。
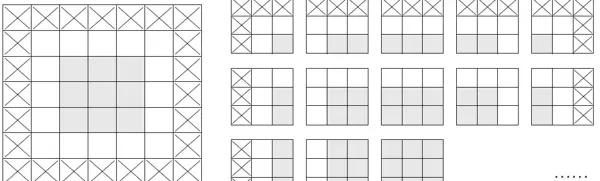 在Conv2D层中,通过设置`padding`参数来控制是否填充。该参数有两个常见取值:“valid”表示不进行填充,只保留有效的卷积位置;“same”则表示填充后输出的宽高与输入相同。默认情况下,`padding="valid"`。
接下来我们考虑另一个影响输出尺寸的因素——步幅(stride)。此前描述的卷积过程均假设相邻窗口之间无间隔移动,即步幅为1。但实际上,步幅是可调节的参数,代表连续两个卷积窗口中心之间的距离。当步幅大于1时,称为步进卷积(strided convolution)。图8-7展示了在一个5×5输入上使用3×3卷积核、步幅为2且未填充的情况。
在Conv2D层中,通过设置`padding`参数来控制是否填充。该参数有两个常见取值:“valid”表示不进行填充,只保留有效的卷积位置;“same”则表示填充后输出的宽高与输入相同。默认情况下,`padding="valid"`。
接下来我们考虑另一个影响输出尺寸的因素——步幅(stride)。此前描述的卷积过程均假设相邻窗口之间无间隔移动,即步幅为1。但实际上,步幅是可调节的参数,代表连续两个卷积窗口中心之间的距离。当步幅大于1时,称为步进卷积(strided convolution)。图8-7展示了在一个5×5输入上使用3×3卷积核、步幅为2且未填充的情况。
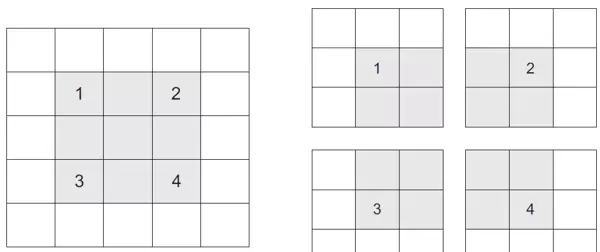 步幅设为2意味着在宽度和高度方向上都进行了2倍下采样(忽略边界影响)。虽然步进卷积在分类任务中较少直接使用,但在某些特定模型结构中具有价值,相关内容将在第9章进一步探讨。对于常规分类网络,通常更倾向于使用最大汇聚(max-pooling)而非步幅卷积来进行下采样。首个卷积神经网络示例中已应用了该操作,下面我们详细说明其原理。
最大汇聚的作用是从输入特征图中提取局部区域,并输出每个通道中的最大值。其工作机制类似于卷积,但区别在于:它使用固定的max运算对局部图块进行变换,而不是依赖可学习的卷积核。一般情况下,最大汇聚采用2×2的窗口并设置步幅为2,以实现特征图的2倍降维;相比之下,标准卷积多采用3×3窗口且步幅为1。
观察前面的卷积神经网络示例可以发现,每经过一个MaxPooling2D层,特征图尺寸就会减半。例如,原本26×26的特征图经最大汇聚后变为13×13。这正是最大汇聚的核心功能——主动降低空间分辨率,实现与步进卷积类似的效果。
那么,为何要对特征图进行下采样?能否去掉最大汇聚层,始终保留较大的特征图呢?我们可以尝试构建一个没有最大汇聚的模型,如代码清单8-5所示:
```
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(inputs)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
outputs = layers.Dense(10, activation="softmax")(x)
model_no_max_pool = keras.Model(inputs=inputs, outputs=outputs)
```
该模型的结构概览如下:
步幅设为2意味着在宽度和高度方向上都进行了2倍下采样(忽略边界影响)。虽然步进卷积在分类任务中较少直接使用,但在某些特定模型结构中具有价值,相关内容将在第9章进一步探讨。对于常规分类网络,通常更倾向于使用最大汇聚(max-pooling)而非步幅卷积来进行下采样。首个卷积神经网络示例中已应用了该操作,下面我们详细说明其原理。
最大汇聚的作用是从输入特征图中提取局部区域,并输出每个通道中的最大值。其工作机制类似于卷积,但区别在于:它使用固定的max运算对局部图块进行变换,而不是依赖可学习的卷积核。一般情况下,最大汇聚采用2×2的窗口并设置步幅为2,以实现特征图的2倍降维;相比之下,标准卷积多采用3×3窗口且步幅为1。
观察前面的卷积神经网络示例可以发现,每经过一个MaxPooling2D层,特征图尺寸就会减半。例如,原本26×26的特征图经最大汇聚后变为13×13。这正是最大汇聚的核心功能——主动降低空间分辨率,实现与步进卷积类似的效果。
那么,为何要对特征图进行下采样?能否去掉最大汇聚层,始终保留较大的特征图呢?我们可以尝试构建一个没有最大汇聚的模型,如代码清单8-5所示:
```
x = layers.Conv2D(filters=32, kernel_size=3, activation="relu")(inputs)
x = layers.Conv2D(filters=64, kernel_size=3, activation="relu")(x)
x = layers.Conv2D(filters=128, kernel_size=3, activation="relu")(x)
x = layers.Flatten()(x)
outputs = layers.Dense(10, activation="softmax")(x)
model_no_max_pool = keras.Model(inputs=inputs, outputs=outputs)
```
该模型的结构概览如下:
 然而,这种设计存在两个显著问题:
首先,它不利于建立特征的空间层级结构。第三层中的3×3感受野仅能覆盖原始输入中7×7范围的信息。这意味着高层特征所感知的视野非常有限,难以捕捉足够大的语义模式来完成数字识别任务——试想仅凭7×7像素的小窗口去判断整个数字图像的内容显然是困难的。理想情况下,最终卷积层应能整合输入全局的信息。
其次,最后一个特征图的维度高达61,952个元素(22×22×128=61,952),数据量过大。这不仅显著增加后续全连接层的参数数量和计算负担,还可能导致过拟合风险上升。
综上所述,合理利用下采样机制(如最大汇聚)对于构建高效、深层的卷积神经网络至关重要。
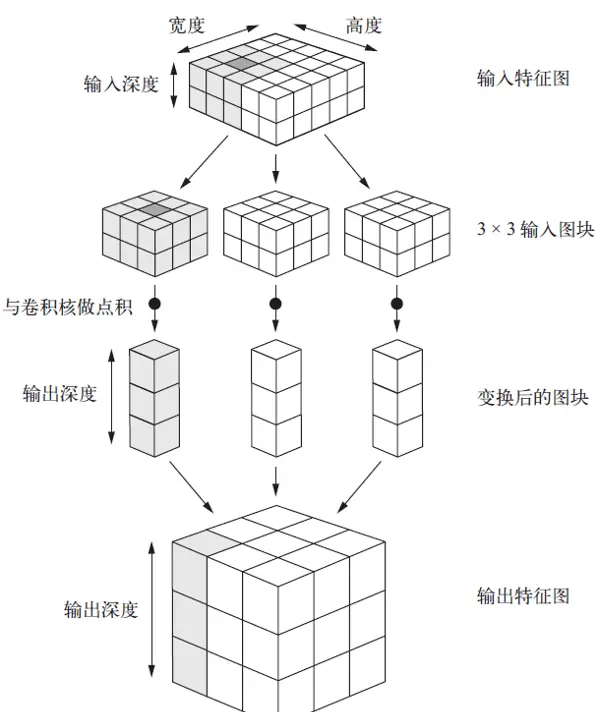
回到最初的示例,使用3×3窗口时,输出向量output[i, j, :]来源于三维输入块input[i-1:i+2, j-1:j+2, :]。整个操作流程参见图8-4。
然而,这种设计存在两个显著问题:
首先,它不利于建立特征的空间层级结构。第三层中的3×3感受野仅能覆盖原始输入中7×7范围的信息。这意味着高层特征所感知的视野非常有限,难以捕捉足够大的语义模式来完成数字识别任务——试想仅凭7×7像素的小窗口去判断整个数字图像的内容显然是困难的。理想情况下,最终卷积层应能整合输入全局的信息。
其次,最后一个特征图的维度高达61,952个元素(22×22×128=61,952),数据量过大。这不仅显著增加后续全连接层的参数数量和计算负担,还可能导致过拟合风险上升。
综上所述,合理利用下采样机制(如最大汇聚)对于构建高效、深层的卷积神经网络至关重要。
回到最初的示例,使用3×3窗口时,输出向量output[i, j, :]来源于三维输入块input[i-1:i+2, j-1:j+2, :]。整个操作流程参见图8-4。
如果你把特征图展平,并在其后接一个输出维度为10的全连接层(Dense层),那么该层的参数数量将超过50万。对于一个结构相对简单的小型模型而言,如此庞大的参数量显然是不合适的,极易引发严重的过拟合问题。
之所以要采用下采样操作,主要有两个目的:其一是降低特征图中需要处理的元素数量,从而减少计算负担并控制过拟合;其二是通过逐层累积的感受野扩大机制,使后续的卷积层能够覆盖原始输入中更大的区域,由此构建出具有层级结构的空间特征提取能力。

需要注意的是,最大汇聚(Max Pooling)并非实现下采样的唯一手段。你可能已经了解,还可以在卷积层中使用步幅(strides)大于1的方式直接缩小特征图尺寸。此外,也可以用平均汇聚(Average Pooling)替代最大汇聚,即对每个局部输入区域在各通道上取均值,而非最大值。然而,在实践中,最大汇聚通常表现更优。这是因为特征图本质上是用来编码某种特定模式或概念在不同空间位置是否存在,而关注这些特征中的最大激活值,相比取平均值,能更有效地保留关键的存在性信息。
更为合理的策略是:首先通过无步进的卷积操作生成密集的特征响应图,然后在局部区域内提取最大激活值作为代表性特征。这种方式比采用带步进的卷积(导致稀疏观测)或对区域取平均(可能弱化显著特征)更具优势,因为它减少了遗漏重要特征的风险。
至此,你应该已经掌握了卷积神经网络的核心组成部分——包括特征图、卷积运算和最大汇聚机制,同时也了解了如何搭建一个基础的小型卷积网络来处理像MNIST手写数字分类这样的简单任务。接下来的内容将转向更具实际价值的应用场景。
 扫码加好友,拉您进群
扫码加好友,拉您进群




 收藏
收藏

