逐行解析Hybrid A*路径规划算法

在自动泊车系统中，路径规划是核心技术之一。传统A*算法虽然高效，但忽略车辆实际运动能力，导致生成的路径无法执行。而混合A*（Hybrid A*）通过引入车辆动力学模型，有效解决了这一问题，特别适用于倒车入库等复杂场景。

以一个典型的斜向停车位为例：车辆需从通道入口处倒车进入车位。若使用传统栅格化的A*算法，所规划出的路径往往包含直角转弯或原地转向动作，这在现实中是不可能实现的。相比之下，Hybrid A*生成的路径具备连续曲率，符合方向盘转动和车轮轨迹的实际约束，真正具备可行驶性。

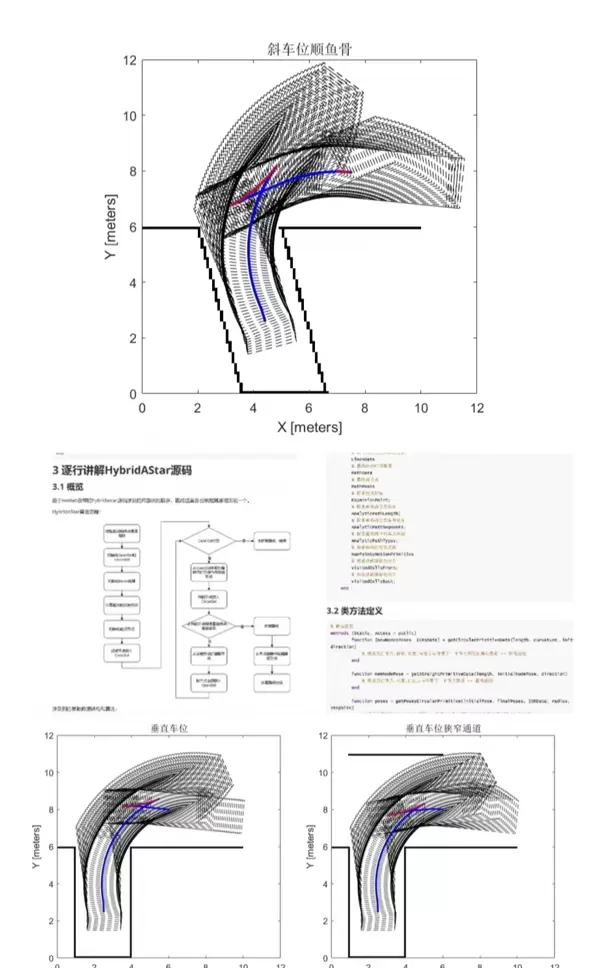
车辆参数与状态建模

在Matlab中实现该算法时，首先需要定义车辆的基本几何与运动参数，如轴距、车长、车宽、最小转弯半径等。这些参数直接影响后续节点扩展的准确性。

vehicle.length = 4.7;  % 车长
vehicle.width = 1.8;   % 车宽
vehicle.wheelbase = 2.8; % 轴距
vehicle.max_steer = deg2rad(40); % 最大转向角

节点结构设计

每个搜索节点不仅包含坐标(x, y)和航向角θ，还需记录到达该状态的成本、父节点索引以及历史路径片段。这种增强型状态表示方式使得算法能够追踪车辆姿态演化过程，是实现运动可行性判断的基础。

function node = createNode(x, y, theta, steer, cost, parent)
    node.x = x;          % X坐标
    node.y = y;          % Y坐标
    node.theta = theta;  % 航向角（弧度）
    node.steer = steer;  % 当前转向角
    node.cost = cost;    % 累计代价
    node.parent = parent;% 父节点索引
end

基于自行车模型的节点扩展

在搜索过程中，后继节点的生成必须遵循车辆运动学规律。采用简化自行车模型模拟前轮转向行为，通过设定多个离散化的方向盘转角指令（如左打、右打、直行），预测下一时刻的位姿变化，从而构建合理的状态转移图。

function successors = generateSuccessors(currentNode, vehicle)
    steer_steps = [-vehicle.max_steer, 0, vehicle.max_steer]; % 左转/直行/右转
    successors = [];
    
    for steer = steer_steps
        % 自行车模型计算新位姿
        R = vehicle.wheelbase / tan(steer);
        dtheta = 0.5 / R; % 步长0.5米对应的角度变化
        
        new_theta = currentNode.theta + dtheta;
        new_x = currentNode.x + 0.5 * cos(new_theta);
        new_y = currentNode.y + 0.5 * sin(new_theta);
        
        % 计算代价时加入转向惩罚
        new_cost = currentNode.cost + 0.5 + 0.3*abs(steer); 
        
        successors = [successors; 
                     createNode(new_x, new_y, new_theta, steer, new_cost, [])];
    end
end

混合启发函数的设计

不同于传统A*仅使用欧氏距离作为启发值，Hybrid A*的启发函数综合考虑了位置距离与航向差异。例如，在目标点附近即使位置接近，若车身方向偏差较大，仍应赋予较高代价，避免误判。这种融合空间与姿态信息的启发策略显著提升了搜索效率与路径合理性。

function h = heuristic(current, goal)
    % 欧式距离部分
    dx = goal.x - current.x;
    dy = goal.y - current.y;
    distance_cost = sqrt(dx^2 + dy^2);
    
    % 航向角偏差惩罚
    theta_diff = abs(wrapToPi(current.theta - atan2(dy, dx)));
    angle_cost = theta_diff * 2;  % 实验调整的权重
    
    h = distance_cost + angle_cost;
end

碰撞检测机制

路径安全性依赖于精确的碰撞检测。算法需将车辆视为具有一定尺寸的多边形，并结合障碍物膨胀后的安全区域进行相交判断。通常采用分离轴定理（SAT）或GJK算法实现高效多边形碰撞检测，确保规划路径全程无接触风险。

function collision = checkCollision(node, map, vehicle)
    % 构建车体四个角点
    car_corners = computeCarCorners(node, vehicle);
    
    % 转换为栅格坐标
    [rows, cols] = size(map.obstacle);
    for i = 1:4
        x_idx = floor(car_corners(i,1)/map.resolution);
        y_idx = floor(car_corners(i,2)/map.resolution);
        
        if x_idx < 1 || x_idx > cols || y_idx < 1 || y_idx > rows
            collision = true;
            return
        end
        
        if map.obstacle(y_idx, x_idx) == 1
            collision = true;
            return
        end
    end
    collision = false;
end

路径平滑优化处理

原始Hybrid A*输出的路径可能存在抖动或不连续曲率现象。为此，在搜索完成后引入二次规划（QP）进行后处理优化。通过对路径节点施加弹性约束，平衡路径长度、曲率变化率和平滑度，最终获得类似人类驾驶员操作的流畅轨迹。

function smooth_path = pathSmoothing(raw_path)
    alpha = 0.5; % 平滑权重
    beta = 0.3;   % 弹性权重
    smooth_path = raw_path;
    
    for iter = 1:100
        for i = 2:length(raw_path)-1
            dx = smooth_path(i+1).x - 2*smooth_path(i).x + smooth_path(i-1).x;
            dy = smooth_path(i+1).y - 2*smooth_path(i).y + smooth_path(i-1).y;
            
            move_x = alpha*(raw_path(i).x - smooth_path(i).x) + beta*dx;
            move_y = alpha*(raw_path(i).y - smooth_path(i).y) + beta*dy;
            
            smooth_path(i).x = smooth_path(i).x + move_x;
            smooth_path(i).y = smooth_path(i).y + move_y;
        end
    end
end

实际部署注意事项

在真实车辆控制系统中应用时，还需进一步考虑执行器动态特性。例如，方向盘转动速度存在物理上限，路径中的曲率突变可能导致控制滞后或乘客不适。因此，建议在路径生成阶段加入对转向速率的限制，提升乘坐舒适性与系统稳定性。

总体来看，经过平滑处理的Hybrid A*路径从“醉汉画线”转变为“老司机操刀”，不仅视觉上更加自然，更重要的是具备了实际可执行性，为自动驾驶泊车功能提供了坚实的技术支撑。