在数值求解偏微分方程中，一维扩散方程是一个典型的模型问题。向前欧拉（FE）、向后欧拉（BE）以及克兰克-尼科尔森（CN）方法是处理此类方程的常用数值格式。本文将基于Matlab平台，分别实现这三种方法对1D扩散方程的求解过程。

1D扩散方程的基本形式

一维扩散方程的标准表达式如下：

\[ \frac{\partial u}{\partial t} = D \frac{\partial^2 u}{\partial x^2} \]

其中，\( u(x, t) \) 表示在空间位置 \( x \) 和时间 \( t \) 处的物理量（如浓度或温度），\( D \) 为扩散系数，描述扩散速率。

向前欧拉（FE）方法

向前欧拉法是一种显式时间积分方案，其离散格式为：

\[ u_i^{n + 1} = u_i^n + \Delta t \cdot D \cdot \frac{u_{i + 1}^n - 2u_i^n + u_{i - 1}^n}{\Delta x^2} \]

该格式利用当前时间步的信息直接计算下一时刻的值，实现简单但需满足稳定性条件（如CFL条件）。

以下是该方法的Matlab实现代码：

% 参数设置
L = 1; % 区域长度
T = 0.1; % 总时间
nx = 101; % 空间节点数
nt = 1000; % 时间步数
D = 1; % 扩散系数

dx = L / (nx - 1);
dt = T / nt;
x = linspace(0, L, nx);
t = linspace(0, T, nt + 1);

u = zeros(nx, nt + 1);
u(:, 1) = exp(-100 * (x - 0.5).^2); % 初始条件

for n = 1:nt
    for i = 2:nx - 1
        u(i, n + 1) = u(i, n) + D * dt / dx^2 * (u(i + 1, n) - 2 * u(i, n) + u(i - 1, n));
    end
    % 边界条件
    u(1, n + 1) = 0;
    u(nx, n + 1) = 0;
end

% 绘图
figure;
for n = 1:nt + 1
    plot(x, u(:, n));
    hold on;
end
xlabel('x');
ylabel('u(x, t)');
title('向前欧拉方法求解1D扩散方程');
hold off;

代码说明：首先设定空间域长度、模拟总时长、网格节点数及扩散系数等参数。使用

linspace

命令生成空间和时间序列。初始化解矩阵，并赋予高斯型初始分布。通过双重循环迭代更新每个空间点上的值，每次更新后施加边界条件（此处设为零）。最后采用动态绘图方式展示不同时刻的演化结果。

向后欧拉（BE）方法

向后欧拉法属于隐式方法，其差分格式为：

\[ \frac{u_i^{n + 1} - u_i^n}{\Delta t} = D \cdot \frac{u_{i + 1}^{n + 1} - 2u_i^{n + 1} + u_{i - 1}^{n + 1}}{\Delta x^2} \]

整理后可转化为线性系统 \( A \mathbf{u}^{n+1} = \mathbf{b} \)，其中 \( A \) 为三对角系数矩阵，\( \mathbf{b} \) 由前一时间步的解构造而成。

对应的Matlab代码如下：

% 参数设置同FE方法
L = 1;
T = 0.1;
nx = 101;
nt = 1000;
D = 1;

dx = L / (nx - 1);
dt = T / nt;
x = linspace(0, L, nx);
t = linspace(0, T, nt + 1);

u = zeros(nx, nt + 1);
u(:, 1) = exp(-100 * (x - 0.5).^2);

% 构建系数矩阵A
A = zeros(nx, nx);
A(1, 1) = 1;
A(nx, nx) = 1;
for i = 2:nx - 1
    A(i, i - 1) = -D * dt / dx^2;
    A(i, i) = 1 + 2 * D * dt / dx^2;
    A(i, i + 1) = -D * dt / dx^2;
end

for n = 1:nt
    b = u(:, n);
    b(1) = 0; % 边界条件
    b(nx) = 0;
    u(:, n + 1) = A \ b;
end

% 绘图
figure;
for n = 1:nt + 1
    plot(x, u(:, n));
    hold on;
end
xlabel('x');
ylabel('u(x, t)');
title('向后欧拉方法求解1D扩散方程');
hold off;

代码解析：参数设置部分与FE一致。核心在于构建符合BE格式的系数矩阵 \( A \)，其主对角线与次对角线元素依据离散系数确定。在时间推进过程中，每一步根据已知的 \( u^n \) 构造右端向量 \( \mathbf{b} \)，并应用边界条件修正。随后通过矩阵左除求解 \( \mathbf{u}^{n+1} \)。可视化部分与FE类似，逐帧绘制演化曲线。

克兰克-尼科尔森（CN）方法

CN方法结合了显式与隐式的优点，具有二阶时间精度，其格式为：

\[ \frac{u_i^{n + 1} - u_i^n}{\Delta t} = \frac{D}{2} \left( \frac{u_{i + 1}^{n + 1} - 2u_i^{n + 1} + u_{i - 1}^{n + 1}}{\Delta x^2} + \frac{u_{i + 1}^n - 2u_i^n + u_{i - 1}^n}{\Delta x^2} \right) \]

同样可化为 \( A \mathbf{u}^{n+1} = B \mathbf{u}^n \) 的矩阵形式进行求解。

Matlab实现代码如下：

% 参数设置同前
L = 1;
T = 0.1;
nx = 101;
nt = 1000;
D = 1;

dx = L / (nx - 1);
dt = T / nt;
x = linspace(0, L, nx);
t = linspace(0, T, nt + 1);

u = zeros(nx, nt + 1);
u(:, 1) = exp(-100 * (x - 0.5).^2);

% 构建系数矩阵A
A = zeros(nx, nx);
A(1, 1) = 1;
A(nx, nx) = 1;
for i = 2:nx - 1
    A(i, i - 1) = -D * dt / (2 * dx^2);
    A(i, i) = 1 + D * dt / dx^2;
    A(i, i + 1) = -D * dt / (2 * dx^2);
end

% 构建矩阵B
B = zeros(nx, nx);
B(1, 1) = 1;
B(nx, nx) = 1;
for i = 2:nx - 1
    B(i, i - 1) = D * dt / (2 * dx^2);
    B(i, i) = 1 - D * dt / dx^2;
    B(i, i + 1) = D * dt / (2 * dx^2);
end

for n = 1:nt
    b = B * u(:, n);
    b(1) = 0; % 边界条件
    b(nx) = 0;
    u(:, n + 1) = A \ b;
end

% 绘图
figure;
for n = 1:nt + 1
    plot(x, u(:, n));
    hold on;
end
xlabel('x');
ylabel('u(x, t)');
title('克兰克 - 尼科尔森方法求解1D扩散方程');
hold off;

代码说明：参数初始化与前述方法相同。本方法需构造两个系数矩阵：\( A \) 对应隐式部分，\( B \) 对应显式部分。在每一时间步中，先通过 \( B \mathbf{u}^n \) 得到右端项，再结合边界条件调整后，求解线性系统获得 \( \mathbf{u}^{n+1} \)。图像输出部分连续展示解的时间演化。

方法对比与总结

三种方法各有特点：

• FE方法 实现简便，无需求解线性系统，但受严格稳定性限制，时间步长必须足够小。
• BE方法 虽为隐式带来较大计算开销，但无条件稳定，适合刚性问题。
• CN方法 在精度与稳定性之间取得良好平衡，兼具二阶精度与无条件稳定性，是高精度需求下的优选方案。

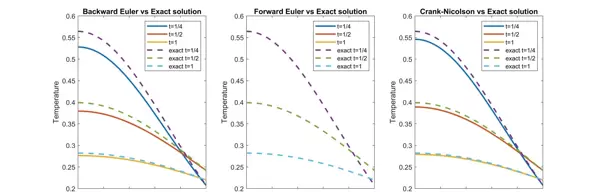
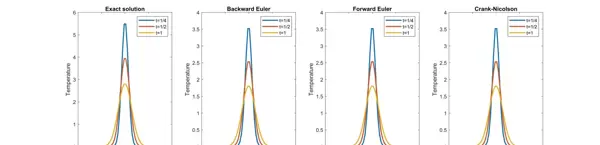
综上所述，针对不同的应用场景和精度要求，可以选择合适的数值策略。通过Matlab编程实现，能够清晰观察到各类方法在求解1D扩散方程中的行为差异与适用范围。