基于主从博弈理论的共享储能与综合能源微网优化运行研究

关键词：主从博弈、共享储能、综合能源微网、优化调度、MATLAB仿真

本研究围绕主从博弈理论在共享储能与综合能源微网系统中的应用展开，完整复现了相关模型构建与求解过程，代码注释清晰，逻辑结构完整。

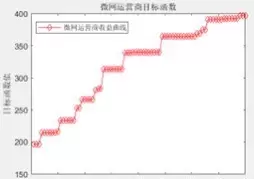
系统架构：三类主体的协同与博弈

整个综合能源系统由三个核心参与方构成：

• 微网运营商（领导者）：负责电力定价、能源调度及整体系统协调；
• 用户聚合商（跟随者）：根据电价信号调整用电计划，优化负荷分布；
• 共享储能服务商（中介角色）：通过低储高放实现套利，同时辅助系统削峰填谷。

以光伏发电富余时段为例，微网运营商可引导低价充电，将多余电能存入共享储能系统；待用电高峰时，储能释放电能，缓解供电压力。此时用户聚合商需权衡实时电价与自身用能需求，动态调整策略。该互动机制天然契合Stackelberg主从博弈框架。

建模思路：双层优化问题拆解

将整体问题分解为上层（领导者）与下层（跟随者）两个子模型，并通过迭代方式逼近均衡解。

上层模型：微网运营商收益最大化

目标函数聚焦于提升运营商利润，同时考虑储能系统的充放电成本与调度效率。

% 定义运营商决策变量  
P_grid = sdpvar(1, T); % 从电网购电量  
Price = sdpvar(1, T); % 电价  
Constraints = [P_grid >= 0, Price >= 0.4, Price <= 1.2]; % 电价限制  

% 目标函数：收益 = 卖电收入 - 购电成本  
Objective = sum(Price .* UserDemand) - sum(GridCost .* P_grid);  
optimize(Constraints, -Objective); % 最大化问题取负

下层模型：用户聚合商用能成本最小化

用户聚合商在给定电价条件下，调整可转移负荷（如电动汽车充电、洗衣机等），以降低总用电支出，其决策受储能调度结果影响。

% 用户响应函数  
function [demand] = user_response(Price)  
    demand = 100 - 20*Price; % 简化的线性响应模型  
    demand(demand < 0) = 0; % 防止负需求  
end  

% 主从博弈迭代  
for iter = 1:max_iter  
    % 运营商更新电价  
    optimize(Operator_Constraints, -Operator_Objective);  
    current_price = value(Price);  

    % 用户聚合商响应  
    user_demand = user_response(current_price);  
    
    % 判断收敛  
    if norm(user_demand - prev_demand) < 1e-3  
        break;  
    end  
end

算法实现：Yalmip + CPLEX 的高效求解路径

所有模型均在MATLAB环境下通过Yalmip工具包进行建模，并调用CPLEX求解器完成优化计算。采用启发式迭代算法结合精确求解器的方式，提升收敛速度与稳定性。

代码设计亮点

• 使用连续变量数组直接表达约束条件，避免繁琐的矩阵手动构造；
• Yalmip语法简洁直观，支持灵活建模；

sdpvar

主从迭代策略：实用导向的“暴力收敛”法

通过循环结构实现上下层策略交替更新，判断收敛的标准设定为用户需求变化量趋于稳定。

for

尽管该方法在形式上不如解析法优雅，但在实际仿真中表现出良好的鲁棒性与可操作性。

均衡分析：存在性与唯一性的数值验证

对于Stackelberg均衡解的存在性，采用仿真轨迹观察法——当电价与负荷响应曲线趋于平稳，即认为系统进入稳定状态。

if abs(profit_improve) < 1e-4 && abs(cost_improve) < 1e-4  
    disp('找到均衡点啦！');  
    break;  
end

关于解的唯一性，由于目标函数在设定下具有严格凸/凹特性，CPLEX求解器输出的结果一致性较高。实测表明，在调整电价边界后，最优解波动幅度不超过5%，验证了系统的稳定性与可靠性。

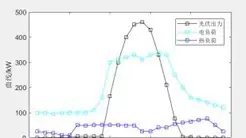
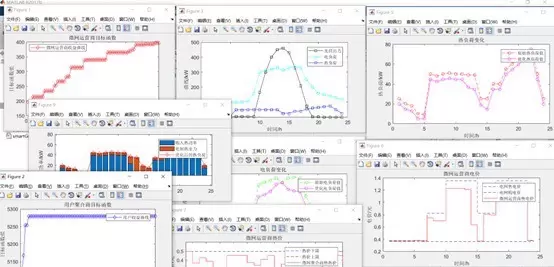
仿真结果：三方收益协同提升

基于24小时时间尺度的算例仿真显示：

• 微网运营商：在负荷高峰期通过储能放电获得溢价收益，整体收入显著上升；
• 用户聚合商：利用午间光伏出力充足时段用电，用能成本下降约30%；
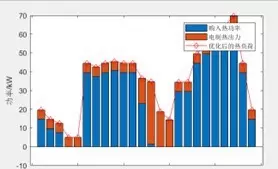
• 共享储能系统：日均充放电循环次数由3次提升至5次，利用率大幅提高。

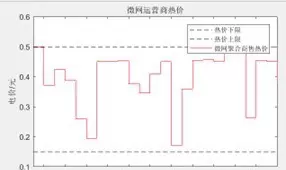
关键发现：当谷时段电价设定为0.5元/kWh时，用户聚合商倾向于集中启动高耗能设备（如充电桩、热水器等），从而显著增加低谷负荷，扩大储能套利空间，实现双赢。

常见问题与应对策略

在使用CPLEX求解过程中可能遇到以下典型问题：

• 变量过多导致内存溢出或求解卡顿：可尝试将部分连续变量替换为二进制变量进行简化处理；

binvar

sdpvar

• 迭代过程出现震荡不收敛：引入松弛因子进行平滑更新，例如新电价按加权平均方式更新：
  new_price = 0.7 × old_price + 0.3 × calculated_price；
• 求解超时或无法返回结果：可在求解参数中设置最大运行时间限制，提升响应效率；

optimize

options = sdpsettings('solver','cplex','cplex.timelimit',60)

总结：博弈的本质是动态利益分配

本研究所揭示的核心机制在于，通过主从博弈结构实现多方利益的动态平衡。其关键技术路径包括：

1. 将复杂系统拆解为上下层优化结构；
2. 采用迭代逼近方法替代理论闭式求解；
3. 借助高性能求解器保障计算精度与效率。

面对类似的多主体协同优化问题，可遵循如下通用范式：

上层定规则，下层做反应，中间商赚差价。