455. 分发饼干

题目描述：
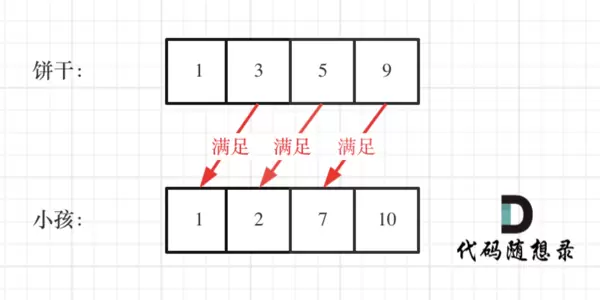
假设你是一位体贴的家长，希望给孩子们分发一些小饼干。每位孩子最多只能获得一块饼干。
每个孩子 i 都有一个胃口值 g[i]，表示能满足该孩子胃口的最小饼干尺寸；每块饼干 j 也有一个尺寸 s[j]。当且仅当 s[j] ≥ g[i] 时，才能将饼干 j 分配给孩子 i，使其得到满足。
目标是尽可能多地满足孩子数量，并返回这个最大值。

示例 1：
输入: g = [1,2,3], s = [1,1]
输出: 1
解释：共有三个孩子，胃口分别为 1、2、3，但只有两块尺寸为 1 的饼干。由于仅胃口为 1 的孩子可被满足，因此最多只能满足 1 个孩子。

示例 2：
输入: g = [1,2], s = [1,2,3]
输出: 2
解释：两个孩子的胃口分别是 1 和 2，而拥有的三块饼干尺寸足以满足所有孩子，故结果为 2。

提示：
- 1 ≤ g.length ≤ 3 × 10
- 0 ≤ s.length ≤ 3 × 10
- 1 ≤ g[i], s[j] ≤ 2 - 1

思路分析：
本题属于贪心算法的经典应用。虽然题干较长，核心逻辑却简单明了：我们有一组不同大小的饼干和一群不同胃口的孩子，目标是最大化被满足的孩子数量。
为了避免浪费较大的饼干资源，应优先匹配大饼干给胃口大的孩子。若将大饼干分配给只需小尺寸的孩子，则可能导致后续无法满足胃口更大的孩子，造成资源错配。
采用贪心策略的具体做法如下：
- 将孩子的胃口数组 g 和饼干尺寸数组 s 均按升序排序；
- 使用双指针从两个数组末尾（即最大值）开始向前遍历；
- 定义计数器记录成功分配的数量；
- 若当前最大的饼干能至少满足当前最大胃口的孩子，则计数器加一，同时移动饼干指针；
- 每次循环中，无论是否完成分配，都必须前移孩子指针——因为当前考虑的是剩余饼干中的最大值，若它都无法满足当前孩子，则更小的饼干也无法满足，因此可以直接跳过该孩子。

通过上述方式，确保每次决策都是局部最优，最终实现整体最优解。

function findContentChildren(g: number[], s: number[]): number {
    g.sort((a, b) => a - b);
    s.sort((a, b) => a - b);

    let childlength:number = g.length
    let cookielength:number = s.length
    let curChild:number = g.length - 1
    let curCookie:number = s.length - 1

    let res:number = 0

    while(curChild >= 0 && curCookie >= 0){
        if(g[curChild] <= s[curCookie]){
            curCookie--
            res++
        }
        curChild--
    }
    return res
};

376. 摆动序列

题目描述：
如果一个数字序列中相邻元素之间的差值严格在正负之间交替变化，则称其为摆动序列。第一个差值可以是正或负。长度小于两个元素的序列也被视为摆动序列。
例如，[1,7,4,9,2,5] 是摆动序列，因其差值序列 (6,-3,5,-7,3) 正负交替；而 [1,4,7,2,5] 不是（前两个差均为正），[1,7,4,5,5] 也不是（最后一个差为零）。
现给定一个整数序列，要求找出其最长摆动子序列的长度。子序列可通过删除部分元素（也可不删）得到，且保持原顺序不变。

示例 1：
输入: [1,7,4,9,2,5]
输出: 6
解释：整个序列本身就是摆动序列。

示例 2：
输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释：存在多个长度为 7 的摆动子序列，如 [1,17,10,13,10,16,8]。

示例 3：
输入: [1,2,3,4,5,6,7,8,9]
输出: 2
解释：单调递增序列中，最多只能保留两个元素形成摆动结构（如首尾两个点）。

思路分析：
使用贪心思想解决此问题的关键在于“去除冗余元素”，从而构造出最长的摆动子序列。
从局部最优角度出发，应尽量减少单调区间内的中间节点，只保留关键转折点（即局部极值点），使得整个序列拥有最多的上下波动次数。
为此引入两个变量：
- prediff：表示前一段的差值，即 nums[i] - nums[i-1]；
- curdiff：表示当前段的差值，即 nums[i+1] - nums[i]。
通过比较这两个差值的符号变化来判断是否存在波峰或波谷。

正常情况下，当 prediff 与 curdiff 异号时，说明出现了方向改变，应计入摆动次数。
但需特别处理以下三种特殊情况：

1. 上下坡中含有平坡（相等元素）：
   如序列中出现连续相同数值，形成平台状结构。此时即使前后有起伏，中间的相等部分不会增加摆动性。
   例如：
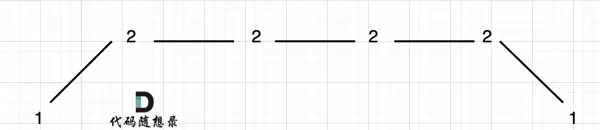
   实际有效摆动长度为 3，中间多个相同的 2 只能保留一个。为了统一处理，可以选择删除左侧或右侧的重复值，这里选择舍弃左边的重复项以简化逻辑。
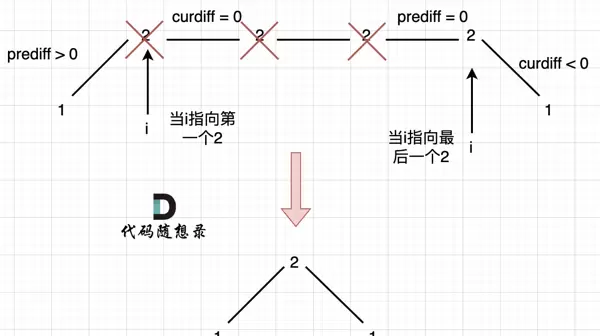
2. 数组起始与结束位置的边界情况：
   序列开头无前驱差值，需单独初始化 prediff；结尾处则需注意最后一次变化是否应被统计。
3. 单调坡度内部包含平坡：
   在持续上升或下降过程中夹杂相等元素，不应误判为波动，仍视为单一趋势的一部分，需忽略其中的平坦段。

结合以上规则，遍历过程中动态更新 prediff 与 curdiff，仅在真正发生符号交替时才累加结果，即可高效求得最长摆动子序列长度。

prediff < 0 && curdiff > 0

prediff > 0 && curdiff < 0

我们先来分析当指向最后一个2时的情况。此时 prediff 等于0，因此必须考虑 prediff === 0 且 curdiff < 0 的情形；同理，curdiff > 0 的情况也应被涵盖。你可以试着将图像旋转180°来理解这一逻辑。由此可见，原先的判断条件并不全面，正确的判断应为：(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，这样才能完整覆盖平坡情况。

接下来看数组的首尾两端。题目中指出，若数组仅有两个不同元素，则摆动序列长度为2。然而，在计算 prediff 和 curdiff 时通常需要三个元素。那么对于仅含两个元素的数组该如何处理？

我们可以将结果 res 初始化为1，相当于默认最右侧已存在一个峰值。以 [2,5] 为例：

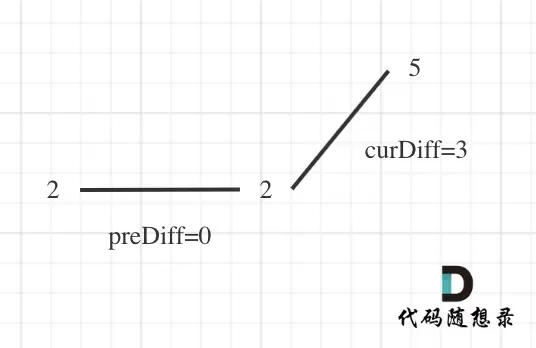
将 res 设为1，相当于假设原数组是 [2,2,5]，这样就构造出了 prediff，且 prediff === 0。此时满足 prediff === 0 并且 curdiff > 0 的条件，于是 res++，最终结果为2，完全符合题意。

据此，我们写出如下代码：

function wiggleMaxLength(nums: number[]): number {
    let prediff:number = 0
    let curdiff:number = 0
    let res:number = 1
    let length:number = nums.length
    if(length <= 1) return length
    for(let i = 0; i < nums.length - 1; i++){
        curdiff = nums[i + 1] - nums[i]
        if((prediff >= 0 && curdiff < 0) || (prediff <= 0 && curdiff > 0)){
            res++
            
        }
        prediff = curdiff
    }
    return res
};

但很快会发现该代码无法通过全部测试用例，原因在于未考虑第三种特殊情况，如图所示：

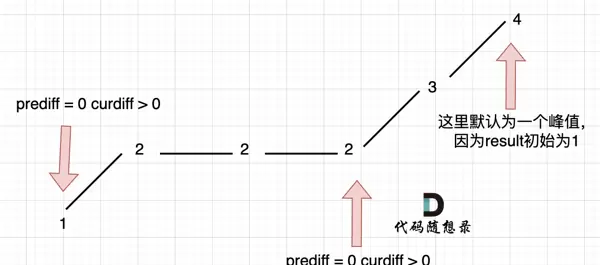
实际上该序列中只有两个峰值，但上述代码会记录三个。问题出在它把单调区间内的平坡也计入了峰值。尽管这些点满足当前判断条件，但本质上属于无效计数。

造成此问题的根本原因是 prediff 被实时更新了。而我们真正希望的是：只有当检测到峰值时才更新 prediff。这样才能避免在单调区间的平坡上误更新 prediff，从而防止后续误判。解决方法很简单——将 prediff 的更新操作移入 if 条件判断内部即可。这样一来，prediff 仅在出现有效峰值时才会被赋新值。

修改后的代码如下：

function wiggleMaxLength(nums: number[]): number {
    let prediff:number = 0
    let curdiff:number = 0
    let res:number = 1
    let length:number = nums.length
    if(length <= 1) return length
    for(let i = 0; i < nums.length - 1; i++){
        curdiff = nums[i + 1] - nums[i]
        if((prediff >= 0 && curdiff < 0) || (prediff <= 0 && curdiff > 0)){
            res++
            prediff = curdiff
        }
    }
    return res
};

53. 最大子数组和

题目描述：
给定一个整数数组 nums，找出一个具有最大和的连续子数组（子数组最少包含一个元素），并返回其最大和。

示例：
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

思路解析：
设想一下，如果数组前两项是 -2 和 1，显然我们应该从 1 开始累加，因为负数只会拉低总和。这正是本题贪心策略的核心所在。

局部最优策略体现在：一旦当前连续和变为负数，立即放弃该部分和，转而从下一个元素重新开始累加。如下图所示：

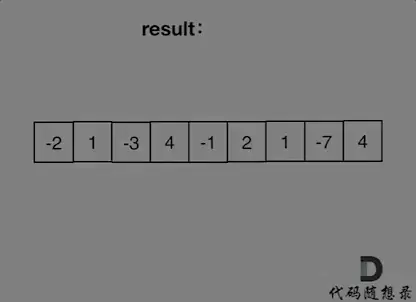
注意，并不是遇到负数就立刻舍弃，而是当“连续和”整体变成负数时才重置。例如图中虽然遇到了 -1，但由于此前的连续和仍为正，继续累加对后续结果有利，因此不会中断。

同时无需担心加入某个负数后会影响最大值判断。因为我们设置了一个变量 res，用于记录遍历过程中出现过的最大连续和。每次更新连续和时都会与 res 比较，只有更大时才会替换。例如图中即使连续和一度为3，res 依然保持为4，确保最终返回的是全局最大值。

还有一个细节需要注意：res 应初始化为负无穷（如 -Infinity），以保证即使第一个元素为负数，也能被正确纳入比较范围。

代码示例：

function maxSubArray(nums: number[]): number {
    let cursum:number = 0
    let res:number = -Infinity
    for(let i = 0, length = nums.length; i < length; i++){
        cursum += nums[i]
        res = Math.max(cursum, res)
        if(cursum < 0) cursum = 0
    }
    return res
    
};

今日总结

今天是学习贪心算法的第一天。这种思维方式确实缺乏统一模板，不像之前的递归或回溯那样有明确的“三部曲”可循。今天这三道题之间关联性不强，解法各异，有些题目即使做出来了，也可能没意识到使用的就是贪心思想，确实有些难以捉摸。不过总体难度尚可，明天继续深入，保持节奏。