1. 引言：误差不可避免，但可被理解

在机器学习的实际应用中，人们常常希望构建一个“完美”的模型。然而，一个看似矛盾却至关重要的事实是：

当模型在训练集上表现得过于出色时，往往在面对新数据时性能会显著下降。

这引出一个根本性问题：模型的预测误差究竟从何而来？哪些部分可以通过优化消除，哪些又是我们必须接受的客观限制？

深入理解误差的来源，是成为高水平机器学习实践者的关键第一步。本文将从基本原理出发，结合经典理论与直观案例，系统剖析模型误差的本质及其内在权衡机制。

2. 模型误差的三类来源（The Three Sources of Error）

根据MIT论文《Neural Networks and the Bias/Variance Dilemma》中的分析框架，模型的总体误差通常可以归结为三个核心组成部分。这一分类为我们理解泛化能力提供了坚实的理论基础。

2.1 Noise：数据固有的"噪声"

本质：Noise来源于真实世界中无法避免的随机波动，存在于输入环境或标签本身，与所选模型无关。它反映的是“理想期望输出”与“实际观测值”之间的差异。

关键洞察：这种误差是不可消除的，构成了模型预测精度的理论下限。无论算法多么先进、数据量多么庞大，Noise始终存在。

生动举例：假设某个文档的真实点击概率为0.2，但我们收集到的训练数据是离散的二元结果（0或1），呈现出类似

[0, 0, 1, 0, 0, ...]

的序列。即使模型准确预测了0.2的概率，在单个样本层面仍会出现如

0 - 0.2

或

1 - 0.2

这样的偏差——这正是Noise的体现。

此外，专家标注也并非绝对一致。例如，对于同一内容，80%的专家可能标记为正类，20%则判为负类，这种主观不一致性同样属于Noise范畴。

2.2 Model-Bias：模型结构固有的"偏差"

本质：这是由于模型自身的表达能力有限而导致的系统性误差。即便拥有无限多且覆盖全面的数据，该误差依然存在。

关键洞察：Bias代表了模型能力的“天花板”。一个简单的线性模型，无论如何调整参数，都无法精确拟合复杂的非线性关系（如正弦函数）。

简单理解：就像用一把直尺去测量弯曲瓶子的周长——无论操作多么精细，工具本身的局限决定了结果必然存在系统性偏差。

2.3 Variance：数据不足导致的"方差"

本质：Variance源于训练数据量不足，使得模型过度适应当前训练集中的偶然模式和噪声，而非学习普适规律。

关键洞察：Variance是过拟合现象的根本原因，表现为模型对不同训练集的高度敏感性。

通过引入更多高质量、多样化的数据，Variance能够被有效抑制。

简单理解：一名学生为了应付考试，并未掌握核心知识，而是机械背诵了某本习题集的所有题目和答案。一旦考试题稍作变化，他就难以应对；而换一本习题集，他的“解法”也会完全不同——这就是高Variance的表现。

3. 偏差-方差权衡（The Bias-Variance Tradeoff）

在上述三类误差中，Noise是外生且不可控的，因此我们的优化重点集中在如何平衡Model-Bias与Variance之间。这也构成了机器学习中最核心的矛盾之一——偏差-方差权衡。

3.1 数学本质：泛化误差的分解

通过对回归任务中期望泛化误差进行数学推导，我们可以将其精确拆解为以下三项之和：

E[(y - \hat{y})^2] = \text{Bias}(\hat{y})^2 + \text{Var}(\hat{y}) + \sigma^2

• \text{Bias}(\hat{y})^2：对应于Model-Bias的平方项，表示模型平均预测与真实函数之间的偏离程度。
• \text{Var}(\hat{y})：即Variance，衡量模型在不同训练集上的预测波动幅度。
• \sigma^2：即Noise，代表标签本身的随机扰动。

这个公式从理论上明确了总误差由三个独立成分构成，为后续调优提供明确方向。

3.2 核心权衡：模型复杂度的双重效应

模型复杂度是调节Bias与Variance之间平衡的关键“旋钮”，但其影响具有两面性：

降低模型复杂度（如采用线性模型）：

• Bias升高：模型灵活性不足，难以捕捉真实的数据规律，容易出现欠拟合。
• Variance降低：模型结构简单稳定，对训练数据的变化不敏感，预测结果更一致。

增加模型复杂度（如使用深度神经网络）：

• Bias降低：更强的表达能力使模型能更好地逼近复杂函数，减少系统性偏差。
• Variance升高：模型变得敏感，容易记住训练集中的噪声和局部特征，导致过拟合风险上升。

4. 演进过程

随着机器学习的发展，研究者逐渐意识到单一追求低训练误差并不可取。早期模型受限于计算能力和数据规模，普遍面临高Bias问题；而现代深度学习时代，则更多面临高Variance带来的挑战。

偏差-方差框架帮助我们跳出“越复杂越好”或“越简单越稳”的片面认知，转而以系统视角审视模型设计。正则化、交叉验证、集成方法等技术的兴起，本质上都是对这一权衡的工程化回应。

5. 实践指南：如何诊断与优化？

在实际建模过程中，应结合训练/验证误差的表现来判断当前处于何种误差主导状态，并采取相应策略：

误差类型	训练误差	验证误差	典型现象	优化策略
高Bias（欠拟合）	高	高	模型太简单，无法拟合训练数据	提升模型复杂度、添加特征、减少正则化
高Variance（过拟合）	很低	远高于训练误差	模型记住了训练样本，泛化差	增加数据量、引入正则化、简化模型、使用Dropout等
Noise主导	较低	接近理论下限	进一步优化效果有限	检查数据质量、重新定义任务目标

6. 总结

为何模型在训练集上难以达到满分？为何测试性能总是低于训练表现？这些问题的答案深植于误差的三大来源之中。

理解Noise、Model-Bias与Variance各自的成因及相互关系，不仅能解释模型行为背后的逻辑，更能指导我们在复杂度选择、数据采集与算法调参等方面做出更明智的决策。

真正的机器学习高手，不是盲目堆叠模型，而是懂得在偏差与方差之间寻找最佳平衡点的人。

我们的目标是找到模型复杂度的“最佳点”，即总误差曲线的最低位置，如下图所示：

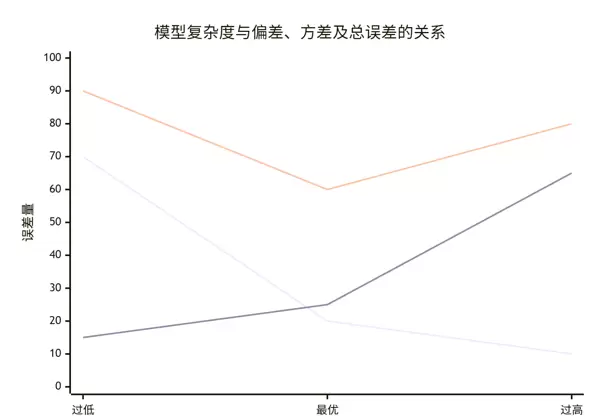
在这一关键权衡中，偏差与方差的变化规律如下：

• Bias降低：当模型具备足够的表达能力时，能够有效捕捉训练数据中的真实模式，从而减少系统性误差。
• Variance升高：随着模型灵活性增强，它可能开始“记忆”训练集中的噪声和随机波动，导致过拟合现象。此时模型对训练数据过于敏感，泛化性能下降，表现出较高的方差。

该理论的发展历程及其应对策略的演进可由以下图谱概括：

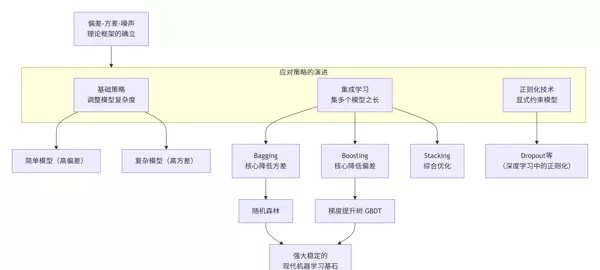
实践指南：如何诊断并优化偏差-方差问题？

理论的意义在于指导实际应用。以下是处理偏差与方差问题的系统性流程：

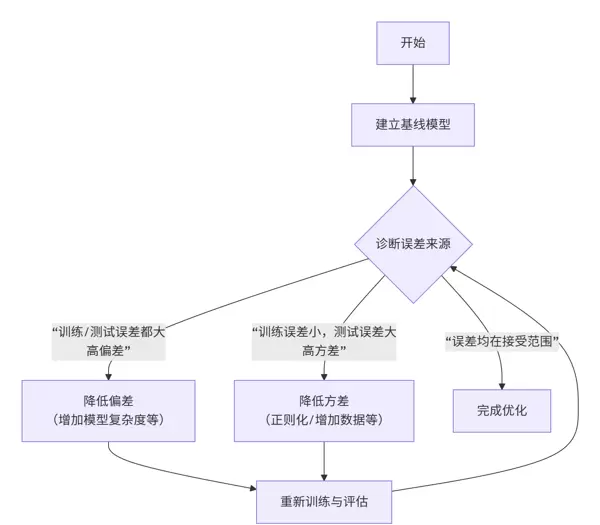
巧妙之处在于：模型优化不应是盲目的参数调整，而应首先识别误差的主要来源——是偏差主导还是方差主导，再采取针对性措施。

诊断与优化策略对照表

现象	诊断	优化策略
训练误差高，验证误差也高	高偏差（欠拟合）	提升模型复杂度（例如从线性模型转向非线性模型） 引入更多有意义的特征 减弱正则化强度
训练误差很低，但验证误差显著偏高	高方差（过拟合）	增加训练样本数量（最有效的手段之一） 加强正则化方法（如L2正则、Dropout） 简化模型结构以降低复杂度 采用集成学习技术（如Bagging）
训练误差与验证误差均较低且接近	偏差与方差达到良好平衡	当前模型表现理想，无需大规模调整

总结

• 接受噪声（Noise）：数据中存在固有的随机波动，这部分无法被模型消除，构成了预测精度的理论下限。
• 理解偏差（Bias）：这是由模型假设不充分引起的系统性误差，需通过选用更合适的模型结构来缓解。
• 控制方差（Variance）：源于模型对训练数据的过度敏感，通常因数据量不足或模型太复杂引起，可通过扩充数据集、使用正则化等手段加以抑制。
• 寻求权衡（Trade-off）：机器学习的核心艺术，在于在偏差与方差之间找到最优平衡点，使二者之和最小，从而最大化模型的泛化能力。