1. 回归算法的基本概念

回归算法属于机器学习中用于预测连续数值结果的一类方法。其主要任务是构建一个数学模型，用以描述自变量（例如年龄、收入、教育水平等）与因变量（如房价、销售额等）之间的映射关系。一旦模型被成功训练，就可以根据新的输入变量来预测相应的输出值。

举例说明：假设我们希望根据一个人的身高来预测其体重。首先需要收集一组包含身高和体重的实际数据样本。基于这些数据，回归算法会拟合出一个能够反映两者关系的数学表达式。此后，对于任意已知身高的个体，即可通过该模型估算其可能的体重范围。

2. Lasso回归简介

Lasso回归，全称为“最小绝对收缩和选择算子”，是一种在线性回归基础上引入正则化机制的改进方法。它通过添加L1正则项来控制模型复杂度，从而有效避免在训练过程中出现过拟合现象。

其核心思想是在优化目标函数时增加一个与回归系数绝对值之和成正比的惩罚项。这一机制不仅限制了系数的大小，还会促使部分不重要特征的系数被压缩至零，实现自动化的特征筛选功能，最终生成一个结构更简洁、可解释性更强的稀疏模型。

主要优势体现在以下两个方面：

• 特征选择： Lasso回归能自动识别并对无关或弱相关特征的系数设为零，相当于从模型中剔除这些变量。这种特性使得模型更加聚焦于关键影响因素，提升了模型的可读性和实用性。
• 防止过拟合： 通过对系数施加约束，降低了模型对训练数据噪声的敏感程度，增强了其在未见数据上的泛化性能。

Lasso的目标函数构成

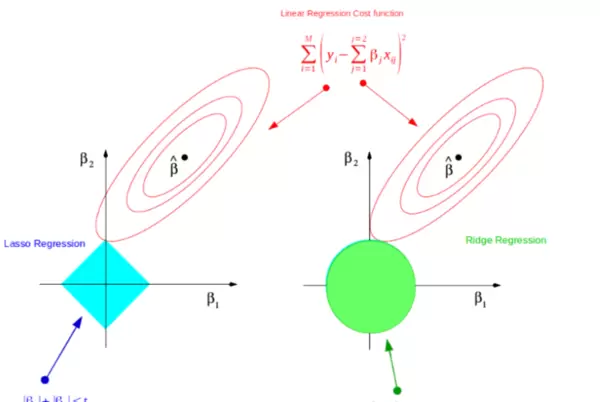
Lasso回归的优化目标由两部分组成：

目标函数 = 残差平方和 + λ × 系数绝对值之和

数学形式如下：

minimize{∑_i=1ⁿ(y_i ∑_j=1^px_ijβ_j) + λ∑_j=1^p|β_j|}

其中：

• 第一部分：∑_i=1ⁿ(y_i ∑_j=1^px_ijβ_j) 表示残差平方和，即模型预测值与真实值之间的误差总和，目的是让模型尽可能贴近训练数据。
• 第二部分：λ∑_j=1^p|β_j| 是L1正则化项，也称惩罚项，用于控制模型复杂度。参数 λ（lambda）决定了惩罚强度——λ 越大，压缩效果越明显，更多系数会被归零，模型越简单。

3. 实际应用案例：房价预测

考虑一个实际场景：我们需要预测某地区房屋的价格（单位：千元），初步认为价格受三个因素影响：房屋面积（平方米）、房间数量以及房龄（年）。现有如下历史数据：

样本编号	面积（平方米）	房间数	房屋年份	房价（千元）
1	120	3	10	300
2	80	2	15	180
3	150	4	8	350
4	200	5	6	500
5	50	1	20	100

步骤1：建立多元线性回归模型

设定房价 y 的预测公式为：

= β + β×面积 + β×房间数 + β×房屋年份

其中，β 为截距项，β、β、β 分别对应各特征的回归系数。

步骤2：构造Lasso优化目标函数

在普通最小二乘法的基础上加入L1正则项。若设定正则化参数 λ = 0.1，则需最小化以下函数：

Minimize{∑_i=1⁵(y_i (β + βx_i1 + βx_i2 + βx_i3)) + 0.1×(|β| + |β| + |β|)}

其中 x_i1, x_i2, x_i3 分别表示第 i 个样本的面积、房间数和房龄。求解该问题后，可得到一组最优系数，部分非显著特征的系数可能被压缩为零。

步骤3：模型训练与特征筛选结果

经过训练后，可能获得如下系数估计（示例值）：

• β = 2（面积的系数较大，说明对房价有显著正向影响）
• β = 0（房间数的系数被压缩至零，表明该变量未被选入最终模型）
• β = -1（房龄系数为负，符合现实逻辑：房屋越新，价格越高）

因此，最终模型简化为：

= β + 2×面积 1×房屋年份

这体现了Lasso回归强大的特征选择能力——自动排除冗余变量，形成更精炼且易于理解的模型结构。

步骤4：新样本预测

现有一套新房，参数为：面积100平方米，房间数3间，房龄12年。使用上述模型进行预测：

= β + 2×100 1×12

假设训练得出 β = 0，则预测房价为：0 + 200 12 = 188（千元）

4. 数学原理深入解析

目标函数的标准表达

Lasso回归的核心在于寻找一组回归系数 β，使得结合了数据拟合精度与模型复杂度的综合目标函数达到最小。该目标函数兼顾了模型对训练数据的拟合能力和结构简洁性，具体形式如下：

minimize ||y Xβ|| + λ||β||

其中，||y Xβ|| 表示残差的L2范数平方，衡量预测误差；||β|| 为回归系数的L1范数（即绝对值之和），代表模型复杂度；λ 控制两者之间的权衡。

总结

综上所述，Lasso回归不仅具备基本的数值预测能力，更重要的是拥有自动特征选择的独特优势。通过将次要特征的系数压缩至零，实现了模型简化，有助于提升模型的可解释性与泛化性能。尤其在面对高维数据、特征冗余较多的情况下，Lasso回归展现出极强的实用价值。

在Lasso回归中，目标函数的形式如下所示：

$$\min_{\beta_0,\boldsymbol{\beta}} \left\{ \frac{1}{2n} \sum_{i=1}^{n} \left( y_i - \beta_0 - \sum_{j=1}^{p} x_{ij}\beta_j \right)^2 + \lambda \sum_{j=1}^{p} |\beta_j| \right\}$$

参数说明：

• n：样本数量。
• p：特征数量。
• y_i：第i个样本的真实值。
• x_ij：第i个样本的第j个特征值。
• β₀：模型的截距项。
• β_j：第j个特征对应的回归系数。
• λ：正则化强度参数，满足 λ ≥ 0。

目标函数的两个组成部分：

1. 均方误差项

表达式为 $\frac{1}{2n} \sum (y_i - \hat{y}_i)^2$。这一部分与普通线性回归一致，衡量的是预测值与真实值之间的平均偏差，目标是最小化该误差以获得更好的拟合效果。

2. L1 惩罚项

形式为 $\lambda \sum |\beta_j|$，即所有回归系数绝对值之和（L1范数）乘以惩罚系数 λ。该项通过压制较大的系数来控制模型复杂度，是Lasso方法的核心机制。

为了简化推导过程，通常会对数据进行中心化处理，从而消除截距项 β₀。此时目标函数可写成矩阵形式：

$$\min_{\boldsymbol{\beta}} \left\{ \frac{1}{2n} \| \mathbf{y} - \mathbf{X}\boldsymbol{\beta} \|_2^2 + \lambda \| \boldsymbol{\beta} \|_1 \right\}$$

其中，$\| \cdot \|_2$ 表示L2范数（欧几里得距离），$\| \cdot \|_1$ 表示L1范数（向量元素绝对值之和）。

求解算法：坐标下降法

由于L1正则项在零点不可导，无法直接对整体目标函数求导得到闭式解。因此，常采用坐标下降法作为Lasso的标准迭代优化策略。

算法思想：

在每次迭代过程中，仅针对某一个系数 β_j 进行优化，其余所有 β_k（k ≠ j）保持不变。通过逐个更新每个参数，循环执行直至收敛。

更新规则推导：

当固定其他系数时，关于 β_j 的子问题可简化为：

$$\min_{\beta_j} \left\{ \frac{1}{2n} \sum_{i=1}^{n} \left( r_i^{(j)} - x_{ij} \beta_j \right)^2 + \lambda |\beta_j| \right\}$$

其中，$r_i^{(j)} = y_i - \sum_{k \neq j} x_{ik} \beta_k$ 称为偏残差，表示当前模型预测结果中去除第 j 个特征贡献后的残差。

通过对该一维问题使用次梯度分析，并令其等于零，可得最优解由一个称为软阈值函数的操作决定：

$$\beta_j^{\text{new}} = S\left( \frac{1}{n} \sum_{i=1}^{n} x_{ij} r_i^{(j)},\; \lambda \right)$$

其中，软阈值函数 $S(z, \gamma)$ 定义如下：

$$S(z, \gamma) = \text{sign}(z) \cdot \max(|z| - \gamma, 0)$$

软阈值函数的直观理解：

该函数将输入值 z 向零收缩 γ 个单位长度。若 |z| ≤ γ，则输出为 0；否则输出为 sign(z)(|z|γ)。这种机制使得不重要的特征系数被精确压缩至零，从而实现稀疏性——这也是Lasso能够自动完成特征选择的根本原因。

Lasso 回归的核心特性总结：

1. 特征选择能力

借助软阈值操作，Lasso能将无关或弱相关特征的系数强制设为零，实现自动化的变量筛选，生成稀疏模型。

2. 控制模型复杂度

正则化参数 λ 是调节稀疏程度的关键超参数：

• 当 λ = 0 时，Lasso退化为普通最小二乘回归；
• 当 λ → ∞ 时，所有系数均被压缩为零，模型变为仅含截距的常数模型；
• 随着 λ 增大，更多系数变为零，模型变得更简单、更稀疏。

优缺点分析及适用场景

优点：

• 内置特征选择：无需额外步骤即可生成稀疏模型，提升模型可解释性。
• 防止过拟合：通过引入正则化项，有效增强模型在新数据上的泛化性能。
• 计算效率高：配合坐标下降等高效算法，适合处理高维特征数据。

缺点：

• 共线性敏感：当多个特征高度相关时，Lasso倾向于随机保留其中一个，而不会像岭回归那样平均分配权重，可能导致模型不稳定。
• 特征数量限制：当特征数 p 远大于样本数 n 时，Lasso最多只能选出不超过 n 个非零系数，可能遗漏关键变量。
• 估计有偏：为了追求稀疏性，对保留下来的特征系数存在系统性压缩，导致估计结果有偏。

典型应用场景：

• 高维数据分析：如基因测序、文本挖掘等领域，特征维度极高但预期仅有少数起作用。
• 强调模型解释性：需要明确识别出哪些变量对输出具有显著影响的应用场景。
• 稀疏特征结构匹配：原始数据本身具有大量零值（如one-hot编码后的类别特征），Lasso的稀疏输出与其天然契合。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

# 1. 生成模拟数据
np.random.seed(42)
n_samples = 1000
n_features = 10

# 模拟生成宏观经济特征
X = np.random.randn(n_samples, n_features) * 10
columns = [f'feature_{i+1}' for i in range(n_features)]
df = pd.DataFrame(X, columns=columns)

# 设置特征的权重（真实情况会更复杂）
true_weights = np.array([2, -1.5, 3, 0, 0, 4, 0, 0, -2, 1])
y = df.values @ true_weights + np.random.randn(n_samples) * 5 # 加入噪声
df['Stock_Price'] = y

# 2. 数据标准化和特征选择（使用Lasso）
X_train, X_test, y_train, y_test = train_test_split(df[columns], df['Stock_Price'], test_size=0.3, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

lasso = Lasso(alpha=0.1) # 设置L1正则化系数
lasso.fit(X_train_scaled, y_train)

# 获得选择的特征
selected_features = [columns[i] for i in range(n_features) if lasso.coef_[i] != 0]
print(f"Selected features by Lasso: {selected_features}")

# 3. 绘制图形

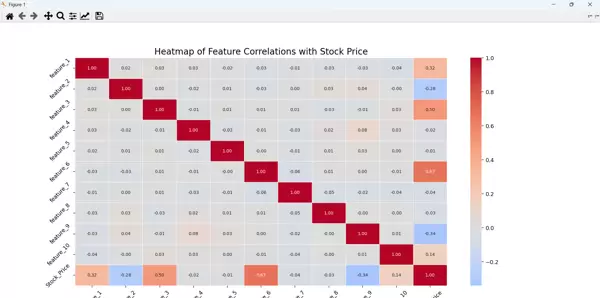
# 图1：各特征与股票价格的相关性热力图
plt.figure(figsize=(12, 8))
correlation = df.corr()
sns.heatmap(correlation, annot=True, cmap='coolwarm', center=0, fmt='.2f', annot_kws={"size": 8}, linewidths=0.5)
plt.title("Heatmap of Feature Correlations with Stock Price", fontsize=16)
plt.xticks(rotation=45)
plt.yticks(rotation=45)
plt.show()

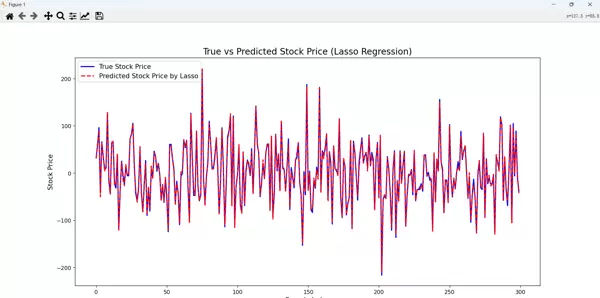
# 图2：预测值和真实股票价格的对比
y_pred = lasso.predict(X_test_scaled)
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}")

plt.figure(figsize=(14, 8))
plt.plot(y_test.values, label="True Stock Price", color='blue', linewidth=2)
plt.plot(y_pred, label="Predicted Stock Price by Lasso", color='red', linestyle='--', linewidth=2)
plt.fill_between(range(len(y_test)), y_test, y_pred, color='purple', alpha=0.3)
plt.title("True vs Predicted Stock Price (Lasso Regression)", fontsize=16)
plt.xlabel("Sample Index", fontsize=12)
plt.ylabel("Stock Price", fontsize=12)
plt.legend(loc='upper left', fontsize=12)
plt.show()