最近在研究基于决策树的手写数字识别系统，整个流程通过Matlab实现，涵盖了图像预处理、特征提取到分类建模的完整环节。项目中包含了定位、5×5网格分割、二值化处理、主成分分析（PCA）以及交叉验证等关键技术，并使用了自制的数据集。配套提供了完整程序与详细报告，共计220页。

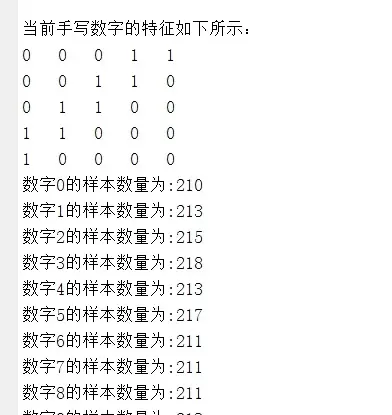
为了构建数据集，特意采购了几包A4纸，邀请室友共同参与手写数字采集。每人书写0-9每个数字各20遍，最终收集了2200张真实手写图像。实际操作发现，真实书写差异极大：有人习惯给7加横杠，有人写0时带小尾巴，这些细节让数据更具挑战性，也更贴近现实场景。

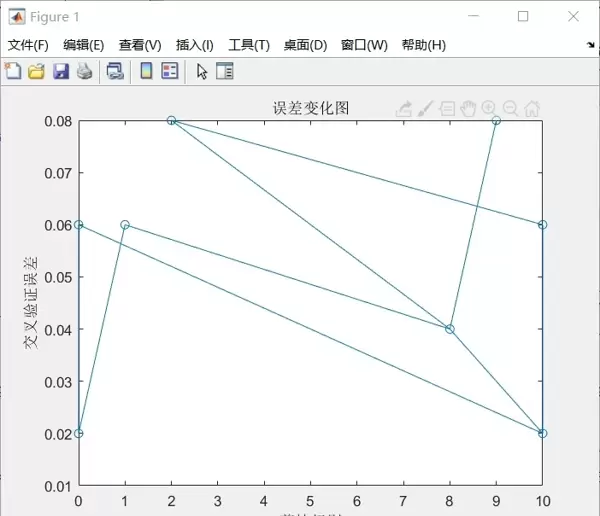
在图像定位阶段，采用形态学闭运算来修复断裂笔画，有效连接断开的边缘。实验表明，使用直径为5像素的圆形结构元素效果最佳。通过regionprops函数检测最大连通区域时，初期常将纸张边缘误判为目标区域。后来在拍摄时引入黑色底板作为背景，显著降低了干扰，提升了定位准确性。

function num_area = locate_num(img)
    gray = rgb2gray(img);
    bw = imbinarize(gray,'adaptive','ForegroundPolarity','dark');
    bw = imclose(bw,strel('disk',5)); % 对付断笔划
    stats = regionprops(bw,'Area','BoundingBox');
    [~,idx] = max([stats.Area]);
    num_area = imcrop(gray,stats(idx).BoundingBox);
end

关于字符分割，最初尝试滑动窗口方法，但效果不稳定。最终改用投影法进行列投影切分，效果明显更优。由于不同数字的宽高比例差异较大——例如“1”通常较窄，“0”则接近正方形，在归一化处理上放弃了保持原始比例的做法，转而统一使用双线性插值将其调整为固定尺寸，结果反而提升了整体识别性能。

cells = zeros(5,5,25); % 5x5网格
[h,w] = size(num_roi);
block_h = floor(h/5); block_w = floor(w/5);
for i = 1:5
    for j = 1:5
        block = num_roi((i-1)*block_h+1:i*block_h, (j-1)*block_w+1:j*block_w);
        cells(:,:,5*(i-1)+j) = imresize(block,[5,5]); % 强制统一尺寸
    end
end

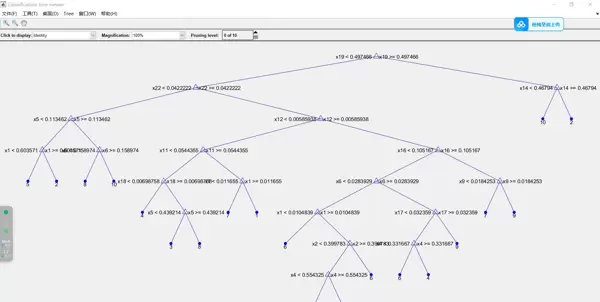
在特征降维方面，采用了主成分分析（PCA）结合随机采样策略，以提升计算效率并减少噪声影响。实验设定保留95%的能量阈值，可将原始25维特征压缩至约12维。令人意外的是，降维后的模型在决策树上的识别准确率反而比使用全特征提高了3%，说明去除冗余信息确实有助于提升泛化能力。

[coeff,score,latent] = pca(reshape(cells,[25,2200])');
keep_dims = find(cumsum(latent)./sum(latent)>0.95,1); % 保留95%能量
features = score(:,1:keep_dims); % 最终得到12维特征

针对决策树模型的参数调优过程中，发现当MinParentSize设置为10、分裂准则（SplitCriterion）选择deviance时，经过交叉验证得到的平均准确率达到89.7%。然而出现一个有趣现象：模型对书写弯曲或风格化的数字识别效果优于工整书写的样本。推测原因在于自制数据集中存在大量“个性化”书写方式，导致模型更适应非标准形态。

tree = fitctree(features, labels, 'CrossVal','on',...
    'MinParentSize',10, 'SplitCriterion','deviance');
loss = kfoldLoss(tree);

为进一步提升稳定性，增加了旋转角度在±15度范围内的数据增强策略，使最终准确率稳定在91%左右。整个项目实践下来最深刻的体会是：特征工程远比模型本身更重要。曾尝试将网格划分从5×5改为7×7，结果准确率不升反降；而在二值化环节改用局部自适应阈值后，“8”的识别率直接跃升至98%。如今看到电话簿上的号码都忍不住想拿程序跑一遍，或许这就是进入状态的标志吧。