在COMSOL中构建激光烧蚀半导体硅的双温方程模型，能够有效模拟微尺度下超快激光与材料相互作用过程。传统传热理论难以准确描述电子系统与晶格系统之间的非平衡能量传递，而双温模型（Two-Temperature Model, TTM）则为此类问题提供了更精确的解决路径。

当激光束扫描硅片表面时，可观察到明显的等离子体辉光现象。这背后是电子系统迅速吸收能量升温，而晶格系统响应滞后所导致的能量失衡状态。为还原这一物理过程，在固体传热模块中需定义两个独立变量：电子温度Te和晶格温度Tl。

电子温度Te的控制方程如下所示：

C_e*Te_t = ?·(k_e*?Te) - G*(Te-Tl) + Q_laser

在参数设置中，已完整配置硅材料的相关特性：电子热容Ce = 3.1e5 × Te（体现温度依赖性），电子热导率ke = 153 × Te/Tl，电子-声子耦合系数G = 1e18 W/(m·K)。特别注意热源项Q_laser的设定，其内嵌了激光脉冲的时间空间分布特征，直接影响能量沉积行为。

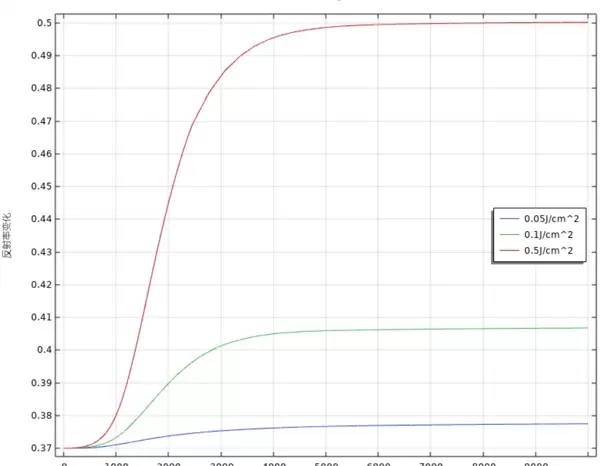
q0 = 1e13 * (1-R) * alpha * exp(-alpha*z)  //R是反射率0.3
时间脉冲用高斯函数：exp(-((t-2e-12)/0.5e-12)^2)

网格划分方面，表面区域必须进行精细化处理。建议在边界层设置厚度为5nm的极薄单元，以捕捉高温梯度区的快速变化。初始条件设置存在一个常见误区——不能直接将电子温度初始化为室温值。正确的做法是依据初始总能量守恒关系反推：E_initial = Ce×300 + Cl×300，从而获得合理的初始Te。

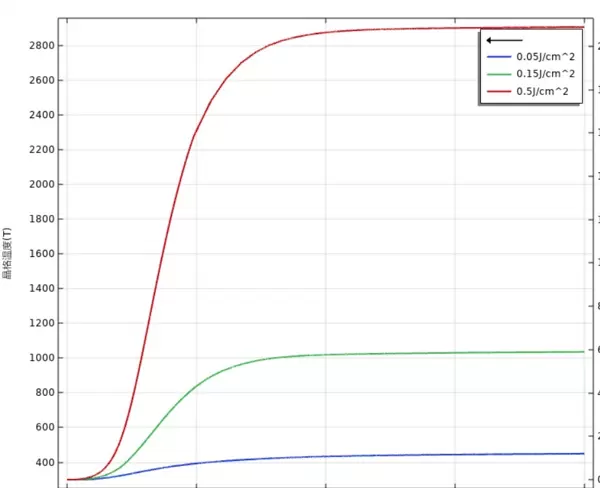
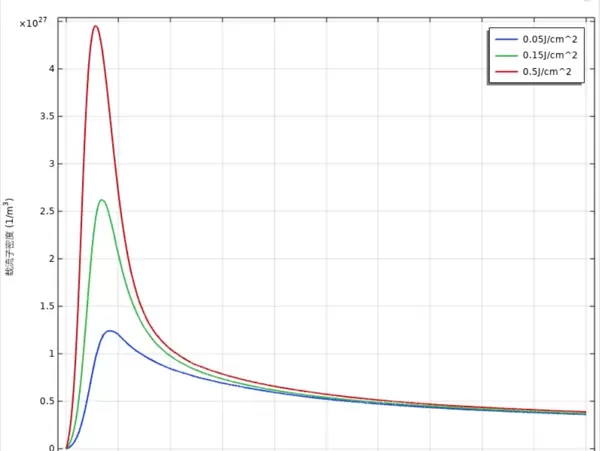
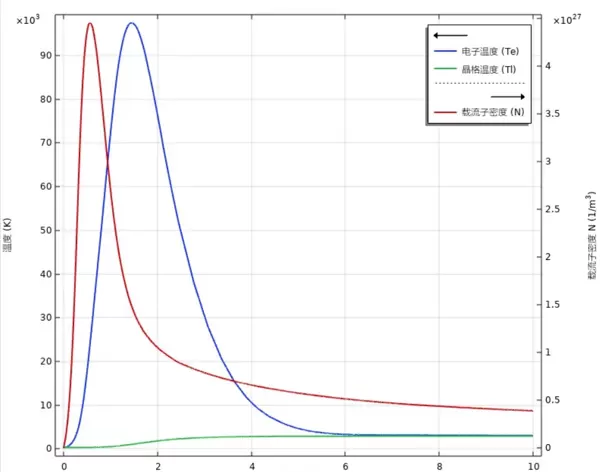
若仿真过程中出现数值振荡，大概率源于时间步长设置过松。推荐将求解器切换至向后差分法（BDF），并将初始时间步长限制在1e-14秒以内，最大步长不超过5e-13秒。从瞬态结果可见（参见温度场动图），电子温度可在200飞秒内跃升至约6000K，而晶格温度仍缓慢上升，尚未突破熔点。这种显著温差正是导致实际烧蚀阈值低于传统预测值的关键原因。

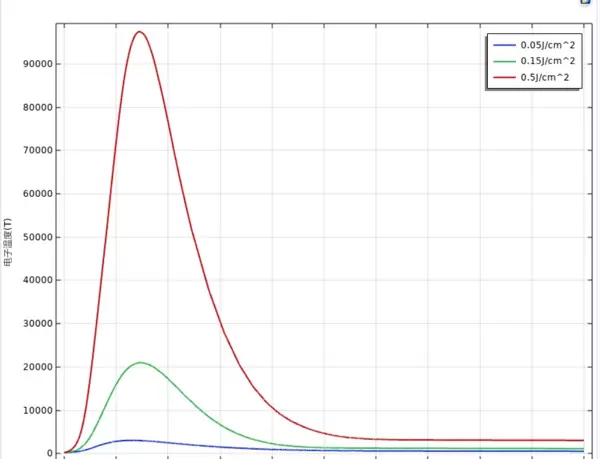
后处理阶段若发现能量守恒误差超过5%，应重点检查是否启用了电子热容的温度相关性设置。此外，建议将Te与Tl之间的温差场单独导出保存，该数据对后续相变、熔融或汽化建模至关重要。根据相关文献研究，当Te达到某一临界值时，带间碰撞机制会改变电子-声子耦合行为。此非线性效应可通过在方程中引入if判断语句实现进阶修正。

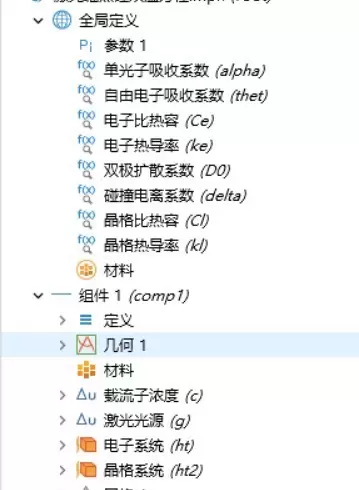
完成建模后，无需手动整理文档。利用软件自带功能，右键点击“生成PDF报告”，系统将自动生成包含模型结构、参数设定及参考文献[1]修正内容在内的完整技术文档。例如，附录B中已详细推导求解稳定性条件，面对晶格温度震荡等问题时，查阅该部分比检索外部论文更为高效。

本案例配套提供详尽的10页PDF文字讲解文件，涵盖模型建立全流程、关键参数来源及物理机制解析。所有硅材料参数均已内置且经过验证，用户无需额外查找资料即可独立开展学习与仿真工作。通过该模型可深入理解激光与半导体相互作用中的非平衡热动力学过程。