矩估计的核心在于通过样本数据来推断总体参数。具体操作时，首先计算总体的数学期望，通常通过对分布列或密度函数进行积分或求和实现。接着将期望表达式中的理论均值 μ 用样本均值 X 替代，参数 θ 则替换为估计量 θ，从而解出矩估计量。这一过程本质上是利用样本矩逼近总体矩，进而反解出未知参数。

在实际应用中，若总体仅含一个未知参数，只需建立一阶矩方程即可；若涉及多个参数（如正态分布中的 μ 和 σ），则需联立一阶与二阶原点矩方程共同求解。例如，对于指数分布 Exp(λ)，其期望为 1/λ，令其等于样本均值 X，可得 λ 的矩估计量为 1/X。该方法步骤清晰、逻辑直接，适合快速应对考试中的填空与计算题型。

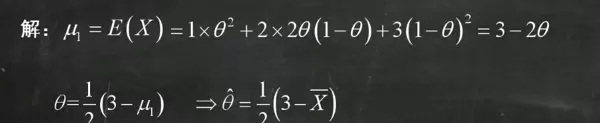
接下来介绍最大似然估计的基本思路：寻找能使观测样本出现概率最大的参数值。不同于矩估计依赖矩的对应关系，MLE 基于概率模型本身，构建所有样本联合发生的概率函数——即似然函数。由于独立同分布假设下联合概率为各概率之积，为便于运算，通常对似然函数取自然对数，将乘积转化为求和形式。

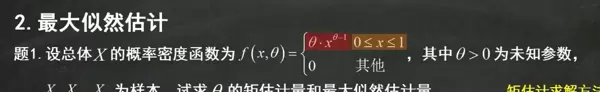
随后对数似然函数对参数 θ 求导，并令导数为零，解得极值点即为候选的最大似然估计值。在此过程中，其他变量视为常数，仅将 θ 视为变量处理。最终所得解中的 θ 替换为 θ，样本符号保持大写形式，完成估计量的构造。

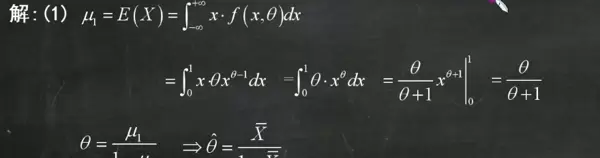
构造似然函数是关键步骤之一。对于连续型分布，使用概率密度函数连乘；离散型则用概率质量函数。取对数后不仅简化了指数运算，也避免了数值溢出问题。整个流程可归纳为：写出似然函数 → 取对数 → 求导 → 解方程 → 得到估计量。这种方法在理论上具有优良性质，如一致性与渐近正态性，因此被广泛应用于统计推断中。

概率论与数理统计 | 矩估计与最大似然估计详解

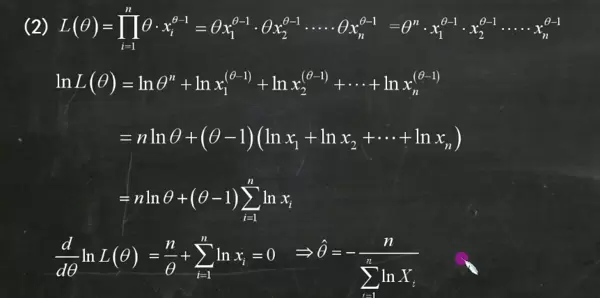
适用对象：理工科及经管类本科学生，正在准备《概率论与数理统计》期末考试的学习者

引言

在参数估计部分，矩估计（Method of Moments, MOM）与最大似然估计（Maximum Likelihood Estimation, MLE）是两大核心内容，常见于选择题、填空题以及综合计算题中。许多同学容易混淆二者使用场景和解题流程，尤其是面对复杂函数时不知如何下手。本文从基本思想出发，梳理标准解法步骤，辅以典型例题解析，帮助你系统掌握这两大点估计方法，提升应试效率。

一、参数估计的必要性

在实际问题中，我们通常已知总体服从某类分布（如正态、指数、泊松等），但其中的关键参数（如 μ, σ, λ）往往是未知的。比如灯泡寿命 X ~ Exp(λ)，虽然知道其服从指数分布，但具体的失效率 λ 需要通过数据估计。

为此，我们需要从总体中抽取样本 X, X, ..., X，利用这些观测值去“推测”真实参数的可能取值，这个过程称为参数估计。根据输出形式不同，可分为：

• 点估计：给出一个具体数值作为参数的估计，如 λ = 0.02
• 区间估计：提供一个置信区间，表示参数可能落在的范围

而矩估计和最大似然估计正是最常用的两种点估计方法。

二、矩估计（Method of Moments）

核心思想：用样本的 k 阶原点矩代替总体的相应矩，建立方程组求解未知参数。

总体 k 阶原点矩定义为 E(X)，样本对应的矩为 (1/n)ΣX。若有 m 个待估参数，则需列出前 m 个矩方程并联立求解。

单参数情况下的解题步骤：

1. 写出总体的一阶原点矩：E(X) = μ(θ)
2. 写出样本一阶原点矩：X = (1/n)ΣX
3. 令两者相等：E(X) = X
4. 解出 θ，得到矩估计量 θ_MOM

三、最大似然估计（MLE）

核心思想：选择使得当前样本观测结果出现概率最大的参数值。也就是说，在所有可能的 θ 中，找出使样本联合密度（或概率）达到最大的那个。

标准解题流程如下：

1. 构造似然函数 L(θ) = ∏f(x; θ)
2. 取对数得到对数似然函数 lnL(θ) = Σlnf(x; θ)
3. 对 θ 求导，其余项视为常数
4. 令导数等于 0，解方程求出 θ
5. 将结果中的 θ 改写为 θ，即得最大似然估计量

此方法虽计算稍复杂，但在大样本下具有一致性、渐近有效性等良好统计性质，是现代统计分析的重要工具。

在参数估计中，最大似然估计（MLE）是一种常用的方法。根据总体分布类型的不同，似然函数的形式也有所区别。

离散型分布：
当样本来自离散型分布时，似然函数定义为：

\[ L(\theta) = \prod_{i=1}^n P(X = x_i; \theta) \]

连续型分布：
若样本来自连续型分布，则似然函数表示为：

\[ L(\theta) = \prod_{i=1}^n f(x_i; \theta) \]

为了便于计算，通常对似然函数取自然对数，得到对数似然函数：

\[ \ln L(\theta) \]

接下来对参数 \(\theta\) 求导，并令导数等于零：

\[ \frac{d}{d\theta} \ln L(\theta) = 0 \]

解该方程可得极大似然估计值 \(\hat{\theta}_{\text{MLE}}\)。

（可选）可通过二阶导数判断是否为极大值点，但在多数情况下此步骤可省略。
注意： 若参数存在定义域限制（例如 \(\theta > 0\)），需额外检查边界情况。

例题 2：指数分布的最大似然估计

设 \(X \sim \text{Exp}(\lambda)\)，求参数 \(\lambda\) 的最大似然估计。

解：

写出似然函数：

\[ L(\lambda) = \prod_{i=1}^n \lambda e^{-\lambda x_i} = \lambda^n e^{-\lambda \sum x_i} \]

取对数得对数似然函数：

\[ \ln L(\lambda) = n \ln \lambda - \lambda \sum_{i=1}^n x_i \]

对 \(\lambda\) 求导：

\[ \frac{d}{d\lambda} \ln L(\lambda) = \frac{n}{\lambda} - \sum_{i=1}^n x_i \]

令导数为 0，解得：

\[ \frac{n}{\lambda} - \sum x_i = 0 \quad \Rightarrow \quad \hat{\lambda} = \frac{n}{\sum x_i} = \frac{1}{\bar{x}} \]

因此，\(\lambda\) 的最大似然估计为：

\[ \boxed{\hat{\lambda} = \dfrac{1}{\bar{X}}} \]

有趣的是，对于指数分布，矩估计与最大似然估计的结果完全相同。

常见分布的参数估计速查表

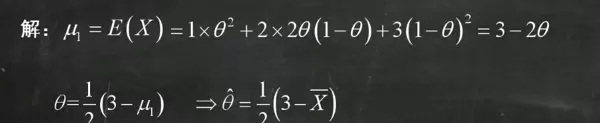
分布	参数	矩估计	最大似然估计
\(N(\mu, \sigma^2)\)	\(\mu\)	\(\bar{X}\)	\(\bar{X}\)
\(N(\mu, \sigma^2)\)	\(\sigma^2\)	\(\frac{1}{n}\sum (X_i - \bar{X})^2\)	\(\frac{1}{n}\sum (X_i - \bar{X})^2\)
\(\text{Exp}(\lambda)\)	\(\lambda\)	\(1/\bar{X}\)	\(1/\bar{X}\)
\(\text{Poisson}(\lambda)\)	\(\lambda\)	\(\bar{X}\)	\(\bar{X}\)
\(U(0, \theta)\)	\(\theta\)	\(2\bar{X}\)	\(\max\{X_i\}\)

重点提示： 对于均匀分布 \(U(0,\theta)\)，其 MLE 是样本中的最大值 \(\max\{X_i\}\)，而非 \(2\bar{X}\)。这是考试中的高频易错点，务必注意。

矩估计与最大似然估计对比总结

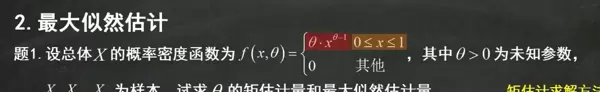
项目	矩估计	最大似然估计
思想	匹配样本矩与总体矩	使观测数据出现的概率最大化
计算难度	较简单（仅需计算期望）	相对复杂（常需求导并解方程）
唯一性	有时不唯一	在正则条件下通常唯一
信息利用程度	较低（仅使用矩信息）	较高（使用完整的概率密度或分布律）
小样本表现	一般	通常更优
期末考查频率	高	极高（常作为大题必考）

期末考试答题模板（大题规范格式）

题目： 设 \(X_1, \dots, X_n \sim U(0,\theta)\)，求 \(\theta\) 的最大似然估计。

标准解答：

总体的概率密度函数为：

\[ f(x;\theta) = \begin{cases} \dfrac{1}{\theta}, & 0 < x < \theta \\ 0, & \text{其他} \end{cases} \]

构造似然函数：

\[ L(\theta) = \prod_{i=1}^n f(x_i;\theta) = \begin{cases} \dfrac{1}{\theta^n}, & 0 < x_i < \theta,\ \forall i \\ 0, & \text{其他} \end{cases} \]

要使得似然函数最大，必须满足所有 \(x_i < \theta\)，即 \(\theta \geq \max\{x_i\}\)。而 \(\frac{1}{\theta^n}\) 随 \(\theta\) 增大而减小，故当 \(\theta = \max\{x_i\}\) 时取得最大值。

因此，\(\theta\) 的最大似然估计为：

\[ \hat{\theta}_{\text{MLE}} = \max\{X_i\} \]

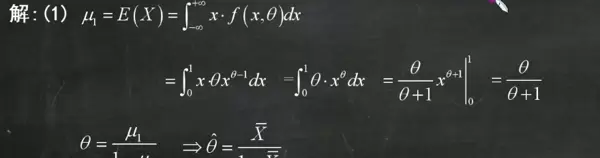
要使似然函数 \( L(\theta) > 0 \)，必须满足条件： \( \theta > \max\{x_1, x_2, \dots, x_n\} \)。 在此条件下，似然函数可表示为：

\[ L(\theta) = \prod_{i=1}^n f(x_i;\theta) = \begin{cases} \dfrac{1}{\theta^n}, & 0 < x_i < \theta,\ \forall i \\ 0, & \text{否则} \end{cases} \]

即当所有样本值都落在区间 \( (0, \theta) \) 内时，\( L(\theta) = \theta^{-n} \)。 由于 \( \theta^{-n} \) 是关于 \( \theta \) 的单调递减函数，因此当 \( \theta \) 取最小可能值时，似然函数达到最大。

故最大似然估计（MLE）为：

\[ \hat{\theta}_{\text{MLE}} = \max\{X_1, X_2, \dots, X_n\} \]

最终结果为：

\[ \boxed{\hat{\theta} = \max\{X_i\}} \]

常见错误提醒

• 忽略似然函数的定义域限制，尤其是在处理均匀分布时未明确写出 \( 0 < x_i < \theta \) 的条件。
• 在对数似然函数求导过程中出错，特别是未能正确将乘积形式转化为求和形式后再求导。
• 误认为样本方差 \( \frac{1}{n}\sum (X_i - \bar{X})^2 \) 不是最大似然估计的结果——实际上，这正是正态分布中方差的 MLE 形式，无需修正。
• 进行矩估计时使用了错误的矩阶数：单参数问题应匹配一阶矩，双参数问题通常需结合一阶与二阶矩。

结语

矩估计与最大似然估计堪称参数估计中的“双子星”。熟练掌握这两种方法，不仅有助于应对期末考试中的综合题型，也为后续学习统计推断、机器学习（例如逻辑回归中的参数估计依赖 MLE）打下坚实基础。

一句话口诀： “矩估匹配期望，似然求导最大；均匀分布要小心，MLE 是最大值！”

下一期内容将深入探讨“估计量的评价标准”，包括无偏性、有效性与一致性等核心概念，敬请期待。

复习建议

• 熟记常见分布（如正态、指数、均匀）的最大似然估计结果。
• 动手完成至少三道不同分布类型的大题练习，强化解题流程与计算能力。
• 注重书写规范，确保每一步推导清晰明了，完整呈现解题过程以争取更多步骤分。