摘要

本文提出一种新颖的知识迁移策略，旨在将预训练深度神经网络（DNN）中的知识进行提炼，并有效地转移至另一个目标DNN中。考虑到DNN通过多层非线性变换逐步将输入映射为输出，作者将所提炼的知识定义为“层间特征流动”，该流动通过计算相邻或指定层级之间特征图的内积来量化。实验结果显示，该方法在多个维度上取得显著成果：（1）采用此知识蒸馏方式训练的学生网络收敛速度明显快于传统从头训练的原始模型；（2）学生网络最终性能超越教师网络；（3）即使教师网络是在不同任务上训练所得，学生网络仍能有效吸收其蒸馏知识，并表现优于随机初始化训练的同类结构。

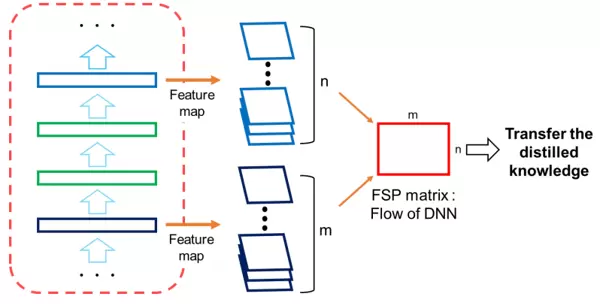
方法概述：基于求解流程的知识提炼

受真实教学过程中教师引导学生掌握解题思路的启发，作者认为，相较于仅传递中间结果，传授“问题解决流程”更能提升模型的泛化能力。在深度神经网络中，这一流程可被理解为各层特征之间的动态关系。由于DNN通过逐层抽象实现信息转换，因此层与层之间的特征关联蕴含了处理逻辑的线索。

为了捕捉这种关系，作者利用格拉姆矩阵（Gram Matrix）——即两个特征图通道间所有空间位置点乘之和所构成的矩阵，来表征特征间的方向性相关性，这与图像中的纹理统计特性相似。通过构建一系列层对之间的FSP（Flow of Solution Procedure）矩阵，实现了对整个网络推理路径的知识建模。

FSP矩阵的数学表达

设Gi,j(x;W)表示在输入x和参数W下，第一个特征层第i个通道与第二个特征层第j个通道之间的相关强度。

其中， 表示第一特征层（如前图中的n层）在空间坐标(s,t)处的第i通道激活值，s对应高度方向，t对应宽度方向。

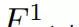
而h×w则代表特征图的空间维度大小，即高度h与宽度w。

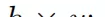
双重求和操作覆盖了两个特征层在全部空间位置上的逐点乘积运算，目的在于衡量两个通道在整个空间范围内的整体响应关联程度。

知识迁移中的损失函数设计

为实现知识的有效迁移，定义了一个基于FSP矩阵差异的损失函数：

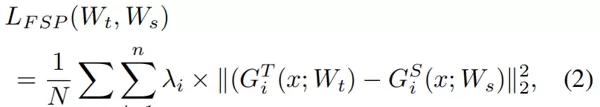
其中N为训练样本总数。

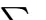
遍历每个输入样本x进行计算。

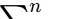
共选取n组不同的层对组合用于FSP矩阵生成（例如n层与m层构成一组）。

λi为第i组层对对应的权重系数，可根据特征重要性调整，关键层对赋予更高权重。

G_T^i(x) 和 G_S^i(x) 分别表示教师网络和学生网络对样本x在第i组层对上生成的FSP矩阵。

损失项采用L2范数的平方形式，即矩阵差值元素平方和，用以最小化师生网络在层间关系层面的差距。

网络结构设计与知识提取位置

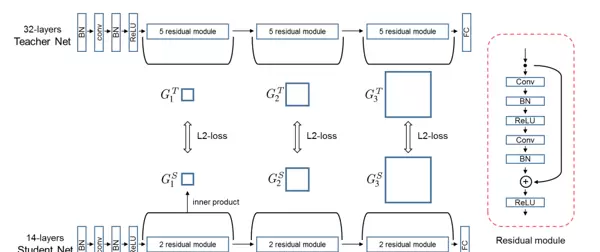
教师网络采用一个32层深的架构，起始部分由「BN → Conv → BN → ReLU」模块组成，随后连接三组“包含5个残差模块”的堆叠结构，最后通过全连接层完成任务输出。在这三组残差块的输入与输出端分别提取特征，生成三个教师端FSP矩阵，用以保存其内部的信息流动模式。

学生网络则为轻量化的14层结构，前端模块与教师一致，但每组残差结构仅包含2个残差模块（少于教师的5个），从而实现模型压缩。尽管结构简化，仍会在与教师相对应的位置提取三组输入-输出特征对，并生成对应的学生FSP矩阵。

值得注意的是，FSP矩阵的生成不依赖于组内残差模块的数量，而是仅需记录每组模块的输入层F1与输出层F2之间的特征关系。因此，无论组内有多少中间层，只要确定首尾两层即可构建相同的FSP表示。

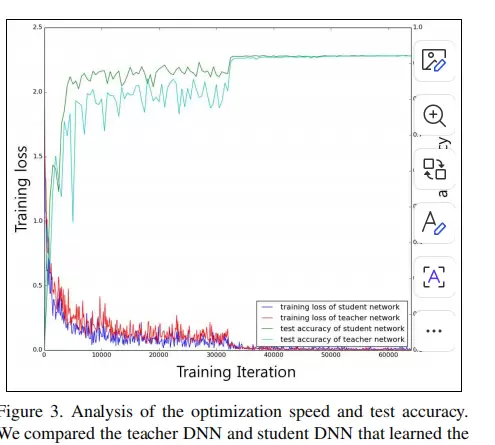
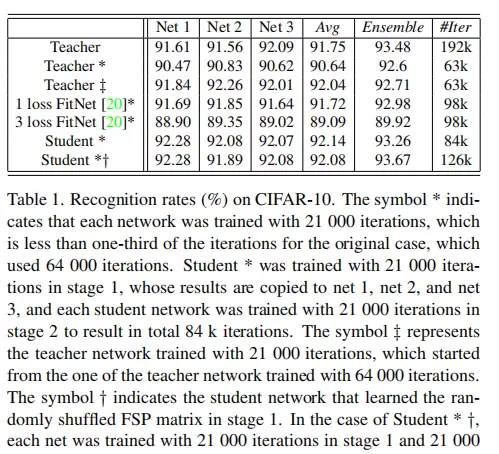
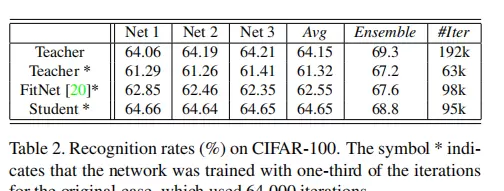
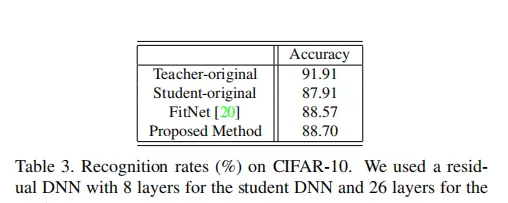
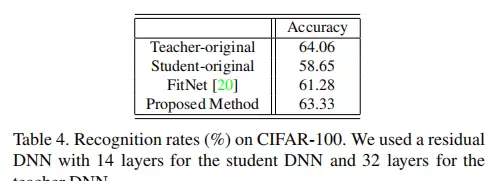
实验设置与可视化展示

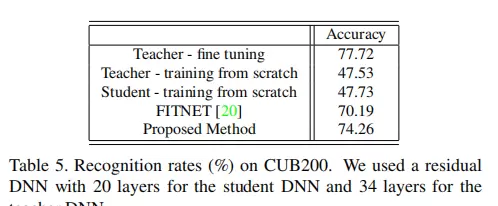
为验证所提方法的有效性，研究进行了多项对比实验，涵盖不同网络规模、任务类型及迁移场景。以下图像展示了实验过程中的关键配置、中间特征分布以及性能比较结果。

结论

本研究提出了一种全新的DNN知识提炼机制，将可迁移知识明确定义为“求解流程”的流动，具体通过FSP矩阵对层间特征关系进行建模。相比传统知识蒸馏方法，该方案更注重网络内部推理路径的复制而非单一输出模仿。实验证明，该方法在三个方面展现出优越性：一是加速学生网络的优化过程；二是提升最终模型性能；三是支持跨任务的知识迁移，即便教师与学生执行不同任务，也能实现有效的知识传递。综上，所提方法为高效、灵活的模型压缩与迁移学习提供了有力工具。