最近在探索八索并联绳索机器人的仿真建模，其基于Matlab的多种模型构建展现出极高的研究价值与技术挑战。本文将围绕该系统中的核心模型展开说明，涵盖运动学、正运动学、力分配以及动力学等方面。

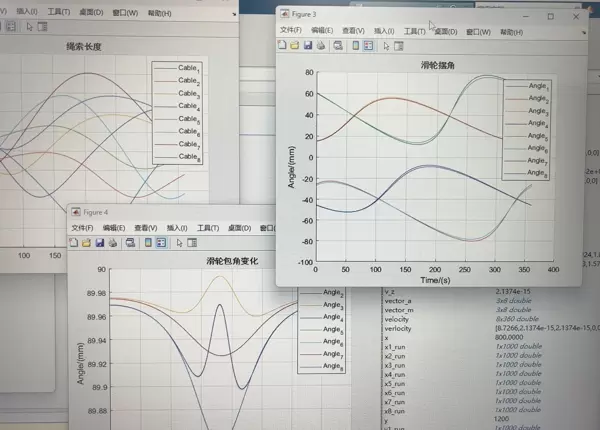
带出绳点滑轮摆动与俯仰的运动学模型是整个系统的基础之一。该模型重点描述滑轮在空间中因绳索牵引而产生的摆动和俯仰行为，这些微小但关键的运动直接影响末端执行器的定位精度。在Matlab环境中，可通过设定几何结构参数与角度变量，结合空间变换方程来实现建模。

% 定义初始参数
l1 = 1; % 某个连杆长度
theta1 = pi/4; % 初始角度

% 计算位置
x = l1 * cos(theta1);
y = l1 * sin(theta1);

例如，在一个简化的示例中，首先设定连杆长度作为结构基础，

l1

并赋予初始角度值，

theta1

然后利用三角函数关系推导出对应点在二维坐标系下的位置坐标，即

x

和

y

。尽管这只是理想化情况下的简单演示，实际应用中需考虑多自由度耦合、空间旋转矩阵及非线性因素，模型复杂度显著提升。

接下来是正运动学模型，它的作用是根据已知的各关节输入（如角度或位移），计算机器人末端的位置与姿态。换句话说，就是从“关节怎么动”推导出“手会去哪”。

% 假设机器人有3个关节，定义关节角度
q1 = pi/6;
q2 = pi/3;
q3 = pi/4;

% 定义连杆长度
a1 = 1;
a2 = 1;
a3 = 1;

% 计算末端执行器位置（这里是简化的2D示例）
x_end = a1 * cos(q1) + a2 * cos(q1 + q2) + a3 * cos(q1 + q2 + q3);
y_end = a1 * sin(q1) + a2 * sin(q1 + q2) + a3 * sin(q1 + q2 + q3);

在示例代码中，给定三个关节角度

q1

、

q2

、

q3

以及对应的连杆长度

a1

、

a2

、

a3

，通过三角运算得出末端在平面上的坐标

和

y

end

。对于八索系统而言，正运动学需处理三维空间中的绳索布局、约束条件和雅可比矩阵，因此通常依赖于更复杂的向量与矩阵运算。

力分配模型则关注如何将整体所需合力合理地分解到八根绳索上，确保每根绳索承担适当的张力，避免松弛或过载。合理的力分配直接关系到系统的稳定性与安全性。

% 假设已知合力F_total
F_total = [10; 5]; % 二维力向量

% 绳索数量
n = 8;

% 初始化力分配向量
F_distribution = zeros(n, 1);

% 简单的力分配算法示例（这里只是示例，实际更复杂）
for i = 1:n
    F_distribution(i) = F_total(1) / n + randn * 0.1; % 加入一些随机扰动模拟实际情况
end

假设总合力为

并初始化一个用于存储各绳索受力的向量

F

distribution

，通过循环结构将合力近似均分，并引入随机扰动以模拟真实工况下的波动。然而，实际建模过程中还需综合考虑绳索张力上下限、机械平衡条件、优化目标函数等因素，常采用线性规划或二次规划等方法求解最优分配方案。

动力学模型用于分析机器人在外部力和内部力矩作用下的加速度响应，揭示“力如何引起运动”的内在机制。它在控制器设计和轨迹跟踪中具有重要作用。

% 定义质量矩阵M
M = [5 0; 0 5];

% 定义科里奥利力和离心力矩阵C
C = [0 0; 0 0];

% 定义重力向量g
g = [0; -9.8];

% 定义关节力矩tau
tau = [10; 10];

% 动力学方程示例（简化的线性模型）
q_ddot = M \ (tau - C * q_dot - g);

在此类模型中，通常定义质量矩阵

M

、科里奥利力与离心力项构成的矩阵

C

、重力影响向量

g

以及施加的关节力矩

tau

，再通过矩阵求逆运算得到关节加速度

q_ddot

。由于八索系统存在柔性绳索、多体耦合和非完整约束等特点，其动力学建模需引入拉格朗日方程或牛顿-欧拉法进行精确推导，计算过程更为繁复。

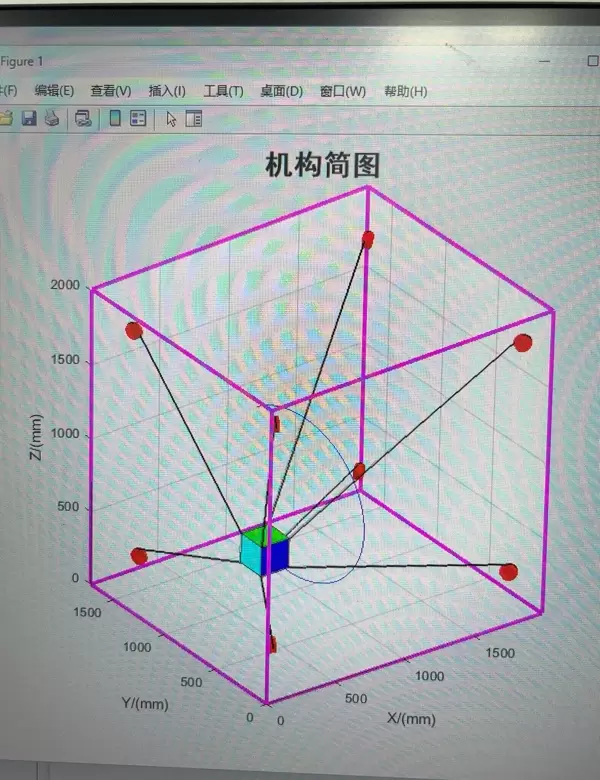
八索并联绳索机器人的Matlab仿真模型体系包含多个相互关联的子模型，每一个都在系统仿真与控制中扮演重要角色。无论是用于理论验证还是工程实践，这些模型共同构建了一个高度逼真的虚拟实验平台，为后续的结构优化、控制策略开发提供了坚实基础。