
立即打开

quantile()和fivenum()的本质差别在于,quantile()函数的算法是采用加权平均,fivenum()是算术平均。这么说可能不易理解,其实很简单的,下面举个例子说明就容易理解了。
例如,一组数据 x <- 11 : 18,则如下图,第一位是11,第二位是12,,,第8位是18,
 对于quantile()算法——加权平均,
0%位是第1位(1+(8-1)*0%=1),值为11;
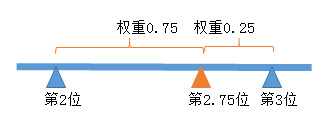
25%位是第2.75位(1+(8-1)*25%=2.75),第2.75位介于第2位和第3位之间,距离哪位较近,哪位数据的权重较大,所以第3位数据的权重是0.75,第2位数据是权重是0.25,则25%位的值=13*0.75+12*0.25=12.75;
对于quantile()算法——加权平均,
0%位是第1位(1+(8-1)*0%=1),值为11;
25%位是第2.75位(1+(8-1)*25%=2.75),第2.75位介于第2位和第3位之间,距离哪位较近,哪位数据的权重较大,所以第3位数据的权重是0.75,第2位数据是权重是0.25,则25%位的值=13*0.75+12*0.25=12.75;
 同理,50%位是第4.5位(1+(8-1)*50%=4.5),值=14*0.5+15*0.5=14.5;
75%位是第6.25位(1+(8-1)*75%=6.25),值=16*0.75+17*0.25=16.25;
100%位是第8位(1+(8-1)*100%=8),值为18;
对于fivenum()算法——算术平均,
同理,50%位是第4.5位(1+(8-1)*50%=4.5),值=14*0.5+15*0.5=14.5;
75%位是第6.25位(1+(8-1)*75%=6.25),值=16*0.75+17*0.25=16.25;
100%位是第8位(1+(8-1)*100%=8),值为18;
对于fivenum()算法——算术平均,
0%位是第1位(1+(8-1)*0%=1),值为11;
25%位是第2.75位(1+(8-1)*25%=2.75),第2.75位介于第2位和第3位之间,用算术平均法,则25%位的值=(13+12)/2=12.5;
同理,50%位是第4.5位(1+(8-1)*50%=4.5),值=(14+15)/2=14.5;
75%位是第6.25位(1+(8-1)*75%=6.25),值=(16+17)/2=16.5;
100%位是第8位(1+(8-1)*100%=8),值为18;
用r语言验证:

quantile()的代码
- x <- 1:100
- n <- length(x)
- probs = seq(0, 1, 0.25)
- index <- 1 + (n - 1) * probs
- lo <- floor(index)
- hi <- ceiling(index)
- x <- sort(x, partial = unique(c(lo, hi)))
- qs <- x[lo]
- i <- which(index > lo)
- h <- (index - lo)
- qs <- (1 - h) * qs + h * x[hi]
- qs
- quantile(x=1:100)
fivenum()的代码
- x <- 1:100
- n <- length(x)
- n4 <- floor((n + 3)/2)/2
- d <- c(1, n4, (n + 1)/2, n + 1 - n4, n)
- 0.5 * (x[floor(d)] + x[ceiling(d)])
- fivenum(x=1:100)
附件列表
![二维码]()
扫码加我 拉你入群
请注明:姓名-公司-职位
以便审核进群资格,未注明则拒绝
相关推荐
栏目导航
热门文章
推荐文章
 扫码加好友,拉您进群
扫码加好友,拉您进群

 扫码加好友,拉您进群
扫码加好友,拉您进群