微观粒子的自旋，纯粹是一个量子理论中才有的特有概念，没有经典对应物。尽管人们经 常将自旋类比于经典物理中的自转（比如地球），但这种比喻只在一定程度上可用。或者 说，自旋是微观粒子的内禀属性，不能用经典转动的图景来解释。除此之外，电子自旋还 有好些不符合经典规律的量子特征。

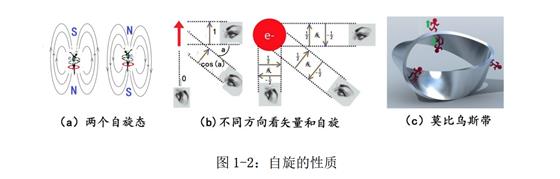
比如说，经典物理中的角动量（比如自转角动量）是三维空间的一个矢量。我们可以在不 同的方向观察这个矢量而得到不同的投影值。如图 1-2b 左图中朝上的红色经典矢量，当 我们从右边观察它时，它的大小是 1；从下面观察时，投影值为 0；而从某一个角度 a 来 观察的话，则得到从 0 到 1 之间随角度连续变化的 cos(a)的数值。

电子的自旋就不一样了。自旋角动量是量子化的，无论你从哪个角度来观察自旋，你都可 能得到、也只能得到两个数值中的一个：1/2，或-1/2，也就是所谓的‘上’，或‘下’。

我们将自旋的“上、下”两种状态叫做自旋的本征态。而大多数时候，电子是处于两种状 态并存的叠加态中。

电子自旋角动量可看作是二维复数空间的矢量。或者说，它的运算规律可以被归类为“旋 量”。旋量在某种意义上可以看成是“矢量的平方根”。不过，这句话听起来照样不好理 解，矢量哪来的平方根呢？

比如，一个二维空间的矢量可以与一个复数相对应，那么，我们或许可以从复数的平方根 来理解“矢量的平方根”。一个复数可以用它的绝对值大小（模）及幅角来表示，如果要 求这个复数的平方根，可将其模值求平方根、幅角减半而得到。因此，一个复数的平方根 的幅角是原来复数幅角的一半。所以，当一个复数（1，0）在复平面上绕着原点转一圈， 即 360 度之后回到它原来的数值时，它的平方根却只转了半圈（180 度），停留在与原来 矢量方向相反的位置上，只有当原复数绕着原点转两圈之后，其平方根复数才转回到原来 的位置。

电子的自旋也具有类似的性质。当自旋在空间中转一圈之后，不是回到原来的状态，而是 上变下，下变上，就像图 1-2c 中的小人在莫比乌斯带上移动一圈之后变成了头朝下的状 态一样。从图 1-2c 中也可以看出，如果那个头朝下的小人继续它的莫比乌斯带旅行，再 走一圈之后，就会变成头朝上而回到原来的状态了。由此可见，电子自旋的这个性质正好 与上面所描述的“矢量平方根”性质相类似。