我想要对3个非平稳的变量建立vecm模型,在此之前需要做协整检验、确定协整秩的个数,同时确定模型的形式是否带漂移项/趋势项(case2/case3/...)。在实际操作中,我用sas得出了如下结论,使用轨迹的协整秩检验和使用限制下的轨迹的协整秩检验给出了不同的秩的个数,请问我应该选择哪个case更好呢?
附1:sas给出的协整检验结果
| 使用轨迹的协整秩检验 |
H0:
Rank=r | H1:
Rank>r | 特征值 | 轨迹 | Pr > 轨迹 | ECM 中的漂移 | 正在进行的漂移 |
| 0 | 0 | 0.3677 | 33.4637 | 0.0182 | Constant | Linear |
| 1 | 1 | 0.2573 | 15.5840 | 0.0483 | | |
| 2 | 2 | 0.0971 | 3.9851 | 0.0459 | | |
[td]
| 使用限制下的轨迹的协整秩检验 |
H0:
Rank=r | H1:
Rank>r | 特征值 | 轨迹 | Pr > 轨迹 | ECM 中的漂移 | 正在进行的漂移 |
| 0 | 0 | 0.4182 | 36.8099 | 0.0326 | Constant | Constant |
| 1 | 1 | 0.2575 | 15.6851 | 0.1889 | | |
| 2 | 2 | 0.0992 | 4.0758 | 0.4014 | | |
[td]
| 限制假设 |
| 假设 | ECM 中的漂移 | 正在进行的漂移 |
| H0(Case 2) | Constant | Constant |
| H1(Case 3) | Constant | Linear |
[td]
| 限制的假设检验 |
| 秩 | 特征值 | 限定的
特征值 | 自由度 | 卡方 | Pr > 卡方 |
| 0 | 0.3677 | 0.4182 | 3 | 3.35 | 0.3413 |
| 1 | 0.2573 | 0.2575 | 2 | 0.10 | 0.9507 |
| 2 | 0.0971 | 0.0992 | 1 | 0.09 | 0.7633 |
附2:vecm的5种形式
Case 1: There is no separate drift in the VECM(p) form.
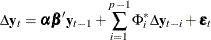
Case 2: There is no separate drift in the VECM(p) form, but a constant enters only via the error correction term.
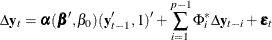
Case 3: There is a separate drift and no separate linear trend in the VECM(p) form.
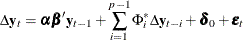
Case 4: There is a separate drift and no separate linear trend in the VECM(p) form, but a linear trend enters only via the error correction term.
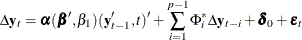
Case 5: There is a separate linear trend in the VECM(p) form.
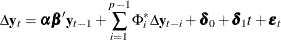

 扫码加好友,拉您进群
扫码加好友,拉您进群