当使用散点图观察自变量（X）和因变量（Y）之间的关系时，数据分布有时看起来像是曲线而不是直线。这种情况下，线性回归并不能很好拟合模型和预测数据，此时就需要对数据进行“改造”，通过各类转换变成线性关系，最终建立回归模型。

1 概念

曲线回归是指对于非线性关系的变量进行回归分析的方法。

曲线回归实际上是将数学关系表达式，转换成线性表达式，然后进行线性回归分析，SPSSAU默认给出转换后的模型结果。

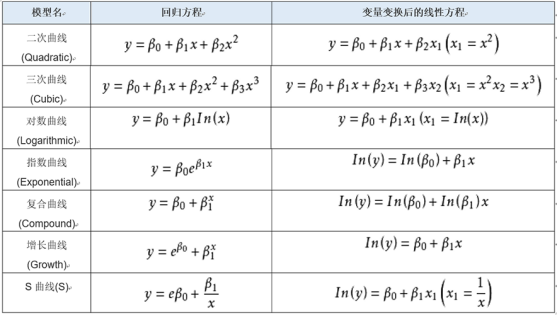
曲线回归方程

SPSSAU共提供其中7种，包括：二次函数、三次函数、对数曲线、指数曲线、复合曲线、增长曲线等。

2 分析步骤

首先第一步，分析前先用散点图确定数据形态；第二步：选择确认好的曲线种类，将变量拖拽到分析框中，点击分析即可。

3 案例分析

1、背景

根据研究要求，在不同温度下，对金属强度进行检测，并找出影响关系。

2、操作步骤

（1）首先通过用散点图确定数据形态。

操作路径：SPSSAU→可视化→散点图

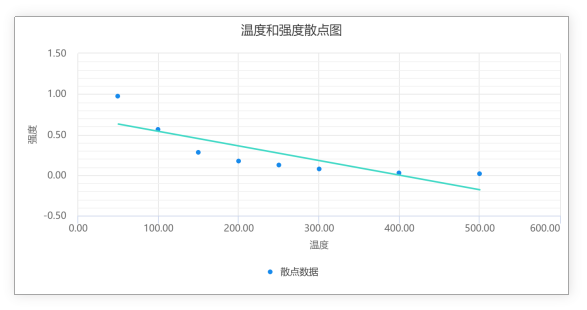
SPSSAU-散点图

可以看到拟合线与散点拟合情况较差，同时很明显的能看出，温度与强度之间存在某种曲线关联（可查看相关文献，得到两者具体关联情况）根据散点分布选择最佳拟合的非线性线。

同一组数据采用不同的曲线方程会得到不一样的拟合效果，如果可以通过文献得知X、Y之间是呈现哪种非线性关系，可直接选择该函数。如果不知道，需要用不同的函数进行分析，结合专业知识对比找出更适合，拟合情况更好的曲线函数。

（2）本例中，选择指数曲线进行拟合。将强度拖拽进“Y分析框”，将温度拖入“X分析框”，点击分析即可。

3、分析结果

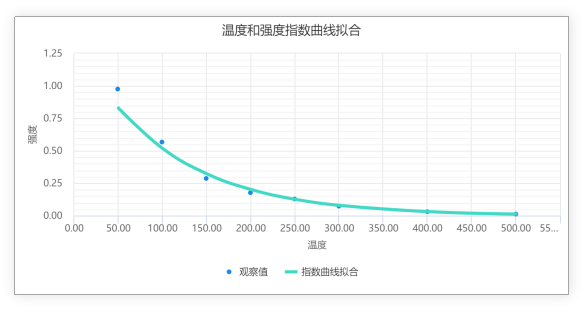
指数曲线拟合图

曲线拟合图直观展示出数据间的拟合关系，上图可以明显的看出，温度和强度之间确实呈现出指数拟合关系。因而也说明数据基本呈现出指数拟合。

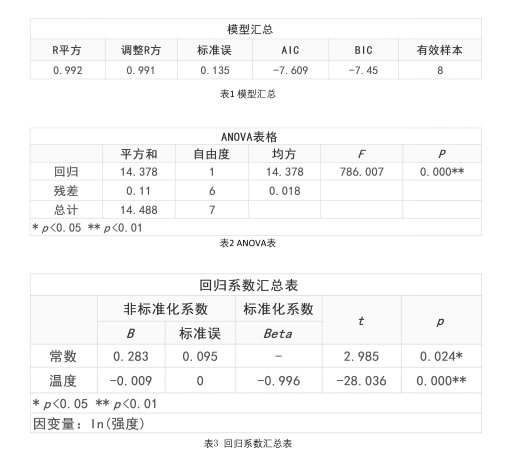
表1用于整体分析模型拟合情况，可以看出，模型R平方值为0.992，意味着模型拟合中有99.2%的数据基本都呈现出指数曲线拟合关系，说明模型拟合程度好。

• 如果需要拟合多种类型的曲线，对比哪个模型更优，可看AIC或BIC指标。AIC或BIC指标是模型对比时使用的常用指标，两个指标值越小越好。

表2是曲线回归ANOVA检验，用于判定模型是否有意义，本例中显示P值<0.05，说明模型有意义。

• 如果上表显示不通过F检验，可考虑使用线性回归或其它曲线类型拟合。

表3为回归系数结果，根据分析结果可知，模型公式为：ln(强度) = 0.283 - 0.009 * 温度

具体分析， 温度对于强度的影响情况来看，自变量时间呈现出0.01水平的显著性，意味着温度会对金属强度产生指数关系的影响，同时回归系数值为-0.009，也说明随着温度的上升，金属强度呈现出指数曲线下降。