交叉熵、相对熵（KL散度）、JS散度和Wasserstein距离（推土机距离）KevinCK Python数据科学信息量：任何事件都会承载着一定的信息量，包括已经发生的事件和未发生的事件，只是它们承载的信息量会有所不同。如昨天下雨这个已知事件，因为已经发生，既定事实，那么它的信息量就为 0。如明天会下雨这个事件，因为未有发生，那么这个事件的信息量就大。从上面例子可以看出信息量是一个与事件发生概率相关的概念，而且可以得出，事件发生的概率越小，其信息量越大。这也很好理解，狗咬人不算信息，人咬狗才叫信息嘛。我们已知某个事件的信息量是与它发生的概率有关，那我们可以通过如下公式计算信息量：假设  是一个离散型随机变量，其取值集合为 χ ,概率分布函数 χ ,则定义事件  的信息量为：  熵：我们知道：当一个事件发生的概率为  ，那么它的信息量是  。那么如果我们把这个事件的所有可能性罗列出来，就可以求得该事件信息量的期望，信息量的期望就是熵，所以熵的公式为：假设 事件  共有 n 种可能，发生  的概率为  ，那么该事件的熵  为：然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为 0-1 分布问题（二项分布的特例），对于这类问题，熵的计算方法可以简化为如下算式： 相对熵（KL 散度）：相对熵又称 KL 散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。在机器学习中，P 往往用来表示样本的真实分布，Q 用来表示模型所预测的分布，那么 KL 散度就可以计算两个分布的差异，也就是 Loss 损失值。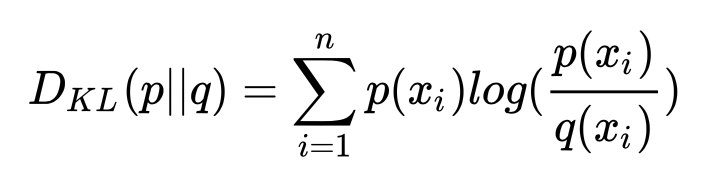从 KL 散度公式中可以看到 Q 的分布越接近 P（Q 分布越拟合 P），那么散度值越小，即损失值越小。因为对数函数是凸函数，所以 KL 散度的值为非负数。有时会将 KL 散度称为 KL 距离，但它并不满足距离的性质：

• KL 散度不是对称的；
• KL 散度不满足三角不等式。
  

交叉熵：我们将 KL 散度公式进行变形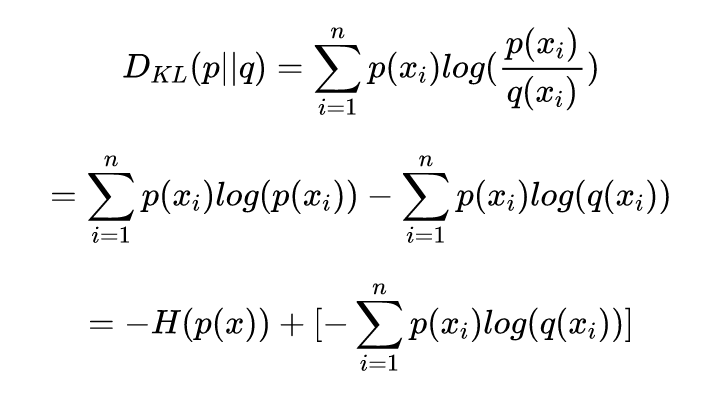：等式的前一部分恰巧就是 p 的熵，等式的后一部分，就是交叉熵：在机器学习中，我们需要评估 label 和 predicts 之间的差距，使用 KL 散度刚刚好，即  ，由于 KL 散度中的前一部分 −H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做 loss，评估模型。JS 散度：JS 散度度量了两个概率分布的相似度，基于 KL 散度的变体，解决了 KL 散度非对称的问题。一般地，JS 散度是对称的，其取值是 0 到 1 之间。定义如下：
Wasserstein 距离（该部分摘自KL 散度、JS 散度、Wasserstein 距离）：KL 散度和 JS 散度度量的问题：如果两个分配 P,Q 离得很远，完全没有重叠的时候，那么 KL 散度值是没有意义的，而 JS 散度值是一个常数。这在学习算法中是比较致命的，这就意味这这一点的梯度为 0。梯度消失了。Wasserstein 距离度量两个概率分布之间的距离，定义如下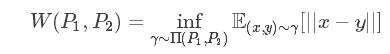Π(P1,P2)是 P1 和 P2 分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布 γ，可以从中采样(x,y)～γ 得到一个样本 x 和 y，并计算出这对样本的距离||x−y||，所以可以计算该联合分布 γ 下，样本对距离的期望值 E(x,y)～γ[||x−y||]。在所有可能的联合分布中能够对这个期望值取到的下界 infγ～Π(P1,P2)E(x,y)～γ[||x−y||]就是 Wasserstein 距离。直观上可以把 E(x,y)～γ[||x−y||]理解为在 γ 这个路径规划下把土堆 P1 挪到土堆 P2 所需要的消耗。而 Wasserstein 距离就是在最优路径规划下的最小消耗。所以 Wesserstein 距离又叫 Earth-Mover 距离。Wasserstein 距离相比 KL 散度、JS 散度的优越性在于，即便两个分布没有重叠，Wasserstein 距离仍然能够反映它们的远近；而 JS 散度在此情况下是常量，KL 散度可能无意义。WGAN 本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布  和  ，  在线段 AB 上均匀分布，  在线段 CD 上均匀分布，通过控制参数  可以控制着两个分布的距离远近。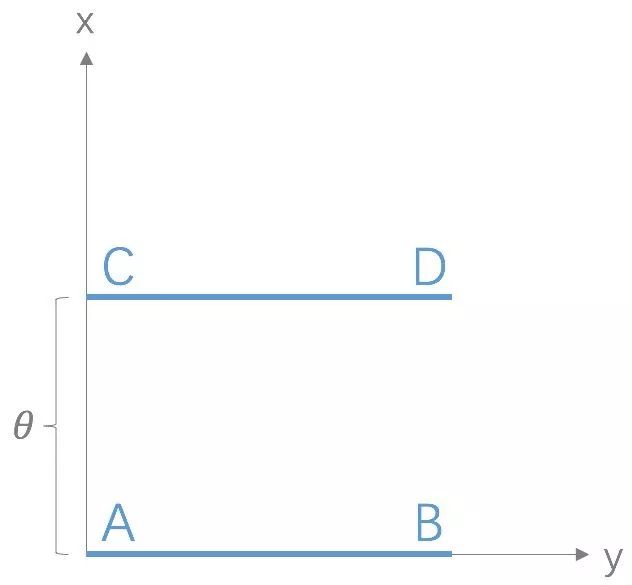此时容易得到（读者可自行验证） （突变） （突变） （平滑）KL散度和JS散度是突变的，要么最大要么最小，Wasserstein距离却是平滑的，如果我们要用梯度下降法优化  这个参数，前两者根本提供不了梯度，Wasserstein距离却可以。类似地，在高维空间中如果两个分布不重叠或者重叠部分可忽略，则KL和JS既反映不了远近，也提供不了梯度，但是Wasserstein却可以提供有意义的梯度。WGAN中对KL散度和JS散度的描述（摘自：郑华滨：令人拍案叫绝的Wasserstein GAN）假设  表示真实样本分布，  是由生成器产生的样本分布。原始GAN中：判别器损失函数：生成器损失函数：（公式）（公式）最优判别器：首先根据公式1，当生成器固定时，确定最优的判别器。对判别器进行求导，并令导数为0，则：化简得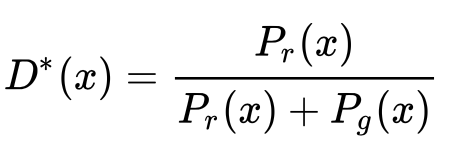：从上述公式也可以很容易看出最优判别器的特征：当  且  ，最优判别器可以给出概率值0，相反，最优判别器可以给出概率值1。生成器损失：普通的GAN在训练时会有一个明显问题，即如果判别器训练的太好，生成器就会完全学不动；那么当判别器为最优时，我们可以通过公式推导生成器的损失函数是怎样。生成器损失函数（1）（公式2）首先给公式2添加一个不依赖生成器的项（真实分布损失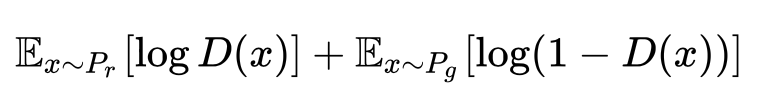：   ）：添加该项后，上式变成了公式1的反，即最小化生成器损失变为了最大化判别器损失。代入最优判别器即公式4，再进行简单的变换可以得到：根据JS散度的公式：于是公式5就可以继续写成：（公式7）公式7即为生产器损失函数1在判别器最优条件下的值。根据原始GAN定义的判别器loss，我们可以得到最优判别器的形式；而在最优判别器的下，我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布 与生成分布 之间的JS散度。我们越训练判别器，它就越接近最优，最小化生成器的loss也就会越近似于最小化 和 之间的JS散度。问题就出在这个JS散度上。我们会希望如果两个分布之间越接近它们的JS散度越小，我们通过优化JS散度就能将 “拉向” ，最终以假乱真。这个希望在两个分布有所重叠的时候是成立的，但是如果两个分布完全没有重叠的部分，或者它们重叠的部分可忽略，那它们的JS散度就变成了 。
换句话说，无论 跟 是远在天边，还是近在眼前，只要它们俩没有一点重叠或者重叠部分可忽略，JS散度就固定是常数 ，而这对于梯度下降方法意味着——梯度为0！此时对于最优判别器来说，生成器肯定是得不到一丁点梯度信息的；即使对于接近最优的判别器来说，生成器也有很大机会面临梯度消失的问题。
生成器损失函数（2）（公式3）上文推导已经得到在最优判别器 下（公式9）我们可以把KL散度（注意下面是先g后r）变换成含 的形式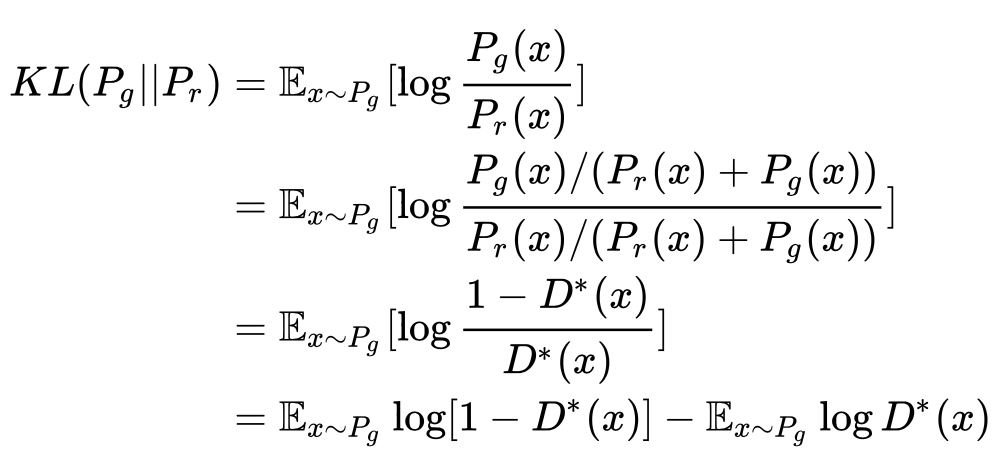：由公式3，9，10可得最小化目标的等价变形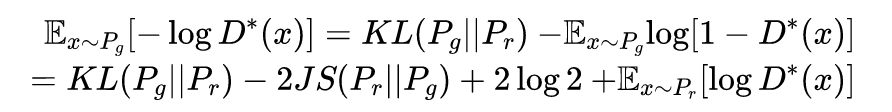注意上式最后两项不依赖于生成器G，最终得到最小化公式3等价于最小化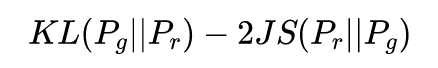这个等价最小化目标存在两个严重的问题。第一是它同时要最小化生成分布与真实分布的KL散度，却又要最大化两者的JS散度，一个要拉近，一个却要推远！这在直观上非常荒谬，在数值上则会导致梯度不稳定，这是后面那个JS散度项的毛病。