一、应用
TOPSIS法用于研究与理想方案相似性的顺序选优技术,通俗理解即为数据大小有优劣关系,数据越大越优,数据越小越劣,因此结合数据间的大小找出正负理想解以及正负理想解距离,并且在最终得到接近程序C值,并且结合C值排序得出优劣方案排序。
二、操作
SPSSAU操作
(1)点击SPSSAU综合评价里面的‘TOPSIS’按钮。如下图
(2)拖拽数据后点击开始分析
三、SPSSAU分析步骤

四、案例
有5个煤矿关于“粉尘浓度”,“二氧化硫量”和“肺病患病率”共3个指标数据;希望通过TOPSIS法对比5个煤矿的优劣性。(TOPSIS有两点需要特别注意,一是数据需要全部同趋势正向化,即数据一定需要越大代表越优(如果不是,则需要SPSSAU数据处理->生成变量功能的逆向化/倒数功能进行处理)数据如下:
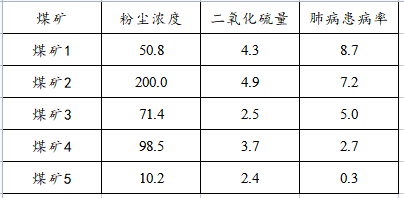
五、数据处理
- 准备好数据,并且进行同趋势化处理(PS:需要研究者自行处理)
- 数据归一化处理解决量纲问题(数据处理->生成变量)
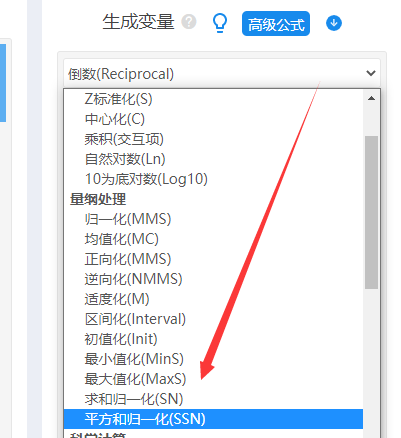
3.经SPSSAU处理后,结果如下
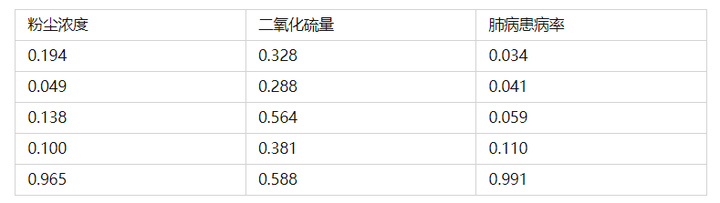
归一化处理后的矩阵为A,记作:

六、结果
SPSSAU生成的分析结果如下:
1.正负理想解

(1)正理想解A+
指标数据中最大值;例:粉尘浓度最大值为0.965;
(2)负理想解A-
指标数据中最大值;例:粉尘浓度最大值为0.049;
- TOPSIS评价计算结果
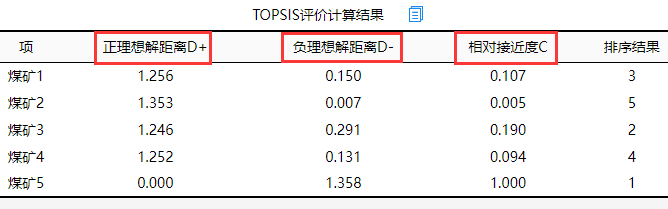
(1)正理想解距离D+
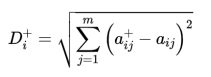
式中,最优方案 ![[公式]](https://www.zhihu.com/equation?tex=+%5Cmathbf%7BA%7D%5E%7B%2B%7D%3D%5Cleft%28a_%7Bi+1%7D%5E%7B%2B%7D%2C+a_%7Bi+2%7D%5E%7B%2B%7D%2C+%5Ccdots%2C+a_%7Bi+m%7D%5E%7B%2B%7D%5Cright%29%EF%BC%9Ba_%7Bi+j%7D) 为矩阵A中元素。
为矩阵A中元素。
(2)负理想解距离D-
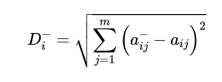
式中,最劣方案 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmathbf%7BA%7D%5E%7B-%7D%3D%5Cleft%28a_%7Bi+1%7D%5E%7B-%7D%2C+a_%7Bi+2%7D%5E%7B-%7D%2C+%5Ccdots%2C+a_%7Bi+m%7D%5E%7B-%7D%5Cright%29) ;
;
(3)相对接近度C
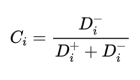
例:0.15/(0.15+1.256)=0.107;
七、总结
综上,针对3个指标(粉尘浓度,二氧化硫量, 肺病患病率),进行TOPSIS评价,同时评价对象为5个(样本量数量即为评价对象数量);
TOPSIS法首先找出评价指标的正负理想解(A+和A-),接着计算出各评价对象分别与正负理想解的距离值D+和D-。
根据D+和D-值,最终计算得出各评价对象与最优方案的接近程度(C值),并可针对C值进行排序。

 扫码加好友,拉您进群
扫码加好友,拉您进群