本期尝试复刻：

Global financial cycle and the predictability of oil market volatility: Evidence from a GARCH-MIDAS model

该研究使用GARCH-MIDAS框架，考察全球金融周期（GFCy）对石油市场波动性的预测能力。这种模型提供了一种适当采样机制，可以在日频的石油波动预测中纳入月频的数据——金融周期（GFCy），解决了宏观变量与金融数据不同频的问题。
该作者提供的代码与数据较为完整：

但是，有一些关键的步骤需要自己补充，还有一些小错误需要调整才能成功复刻。

第一，缺失关键函数——GARCH-MIDAS.m , 需要自备：

第二，缺失 Diebold and Mariano (1995) test的P值的计算方法

该文章比较GARCH-MIDAS-GFCy模型与GARCH-MIDAS-RV基准预测性能基于Diebold和Mariano（1995）测试统计量。

显著为负的测试统计量表明GARCH-MIDAS-GFCy模型优于GARCH-MIDAS-RV模型：

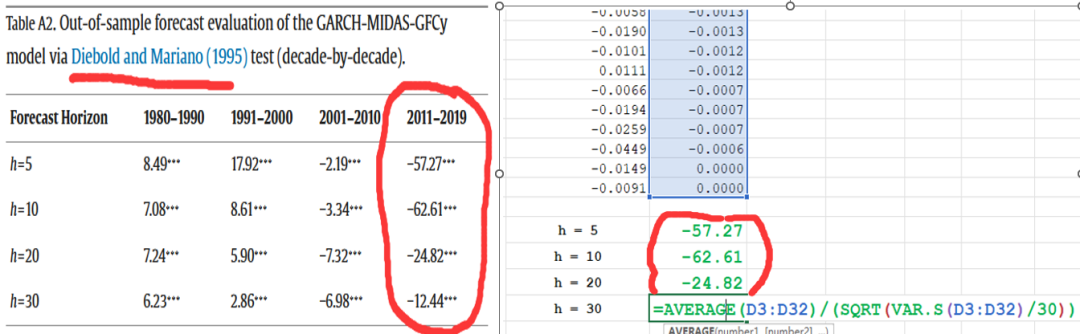
在作者提供的文件中，提供了DM统计量的计算方法，还需补充P值计算：

• 
  

from scipy import stats# 输入自由度和t统计量，以h=10为例df = 10  # 自由度，h值t_statistic = -62.61  # t 统计量# 计算双尾 P 值p_value = 2 * (1 - stats.t.cdf(abs(t_statistic), df))print("P 值:", p_value)

根据计算，使用给定的自由度和 t 统计量，双尾 P 值将会非常接近于零，因为 t 统计量的绝对值非常大。逐个套入不同的自由度与h的值，结论与原文一致。

第三，缺失样本外预测的代码，不熟悉该模型的读者可能会蒙圈

作者在代码中只提供了样本内预测的方法，样本外预测需要自己补充：

• 
  

% Adding out-of-sample forecast n=30outSampleForecast = 30;[estParams_out, EstParamCov_out, Variance_out, LongRunVar_out] = GarchMidas(wti, 'Period', period, 'NumLags', numLags, 'X', xDay, 'ThetaM', 1, 'RollWindow', 1, 'estSample', nobs - outSampleForecast);y_out = NaN(nobs, 1);for t = 1:nobs    if t > nobs - outSampleForecast        y_out(t) = estParams_out(1) + sqrt(Variance_out(t));    endendresidual_out_x = wti - y_out;
[estParams_out, EstParamCov_out, Variance_out, LongRunVar_out] = GarchMidas(wti, 'Period', period, 'NumLags', numLags,  'ThetaM', 1, 'RollWindow', 1, 'estSample', nobs - outSampleForecast);y_out = NaN(nobs, 1);for t = 1:nobs    if t > nobs - outSampleForecast        y_out(t) = estParams_out(1) + sqrt(Variance_out(t));    endendresidual_out = wti - y_out;
xlswrite('PAS_Oil_Gold_GFC_GECON_Residuals.xlsx', residual_out_x, 'DBDA', 'K1:K2104');xlswrite('PAS_Oil_Gold_GFC_GECON_Residuals.xlsx',residual_out,'DBDA','I1:I2104');

用该方法计算出来的数值与论文原文一致 (benchmark model小数点后五位数值有一点偏差，不知道什么原因)：

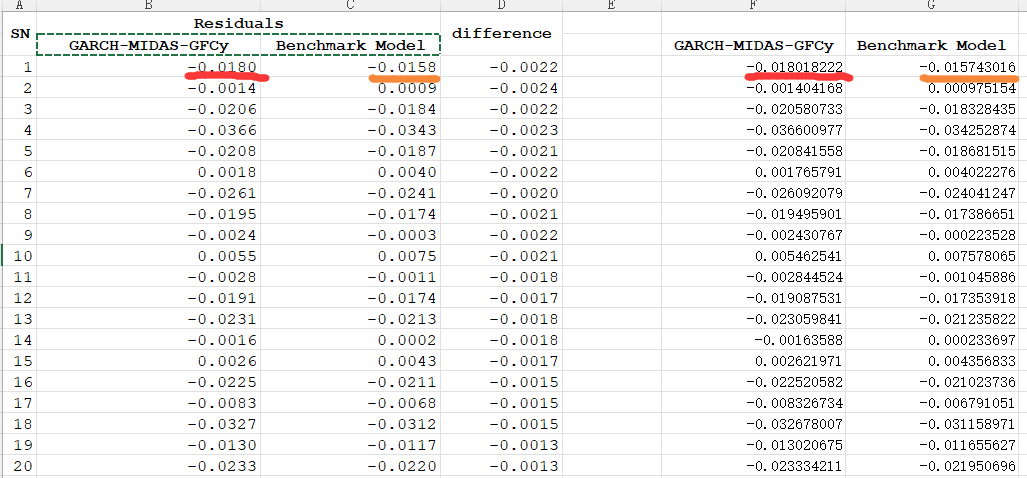
第四，需要解决一个小问题，可能是因为matlab 版本不同的原因引起（也有可能我的函数与作者设置不同）：

在这里把yDate的格式改为正常的 1980/1/17即可。

完成以上步骤，即可完整运行GARCH-MIDAS 样本内、外预测+多模型预测误差比较。

随机测试WTI & GFC 在 Full Sample Data的情况：

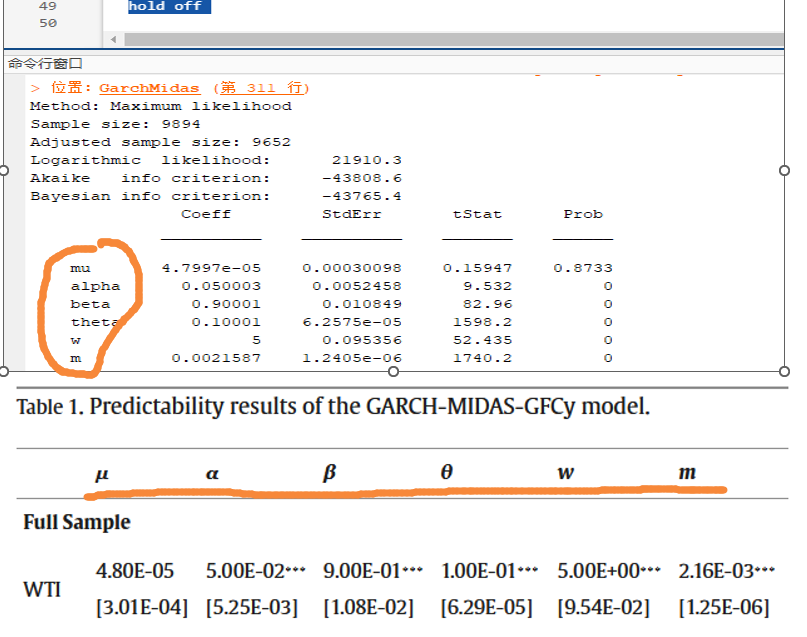
输出系数、显著性和原文没有差异。图片也对应没问题：

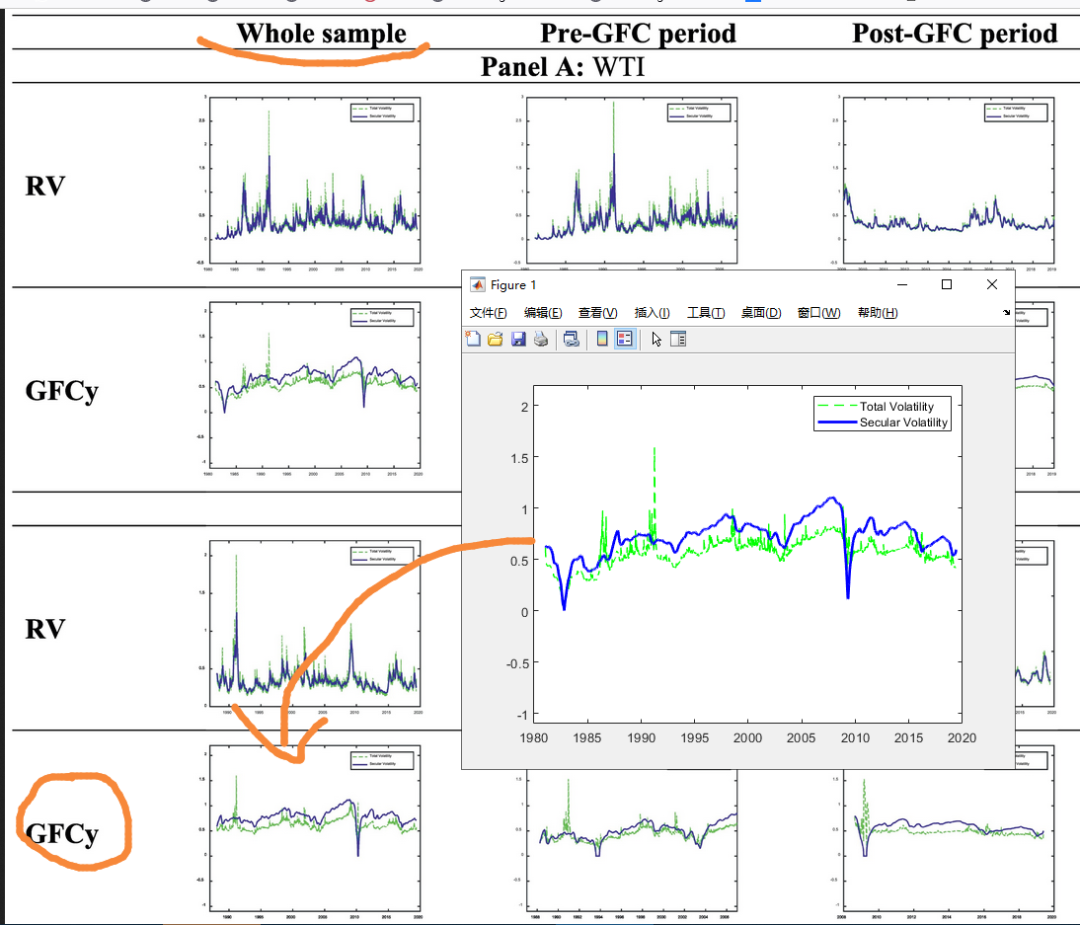
有兴趣的读者可以自行验证其他情况。