基于 Python 的声发射 RA-AF 裂纹模式分析

在材料科学研究领域，利用声发射信号来识别拉伸裂纹（Tensile Crack）与剪切裂纹（Shear Crack）是一项关键任务，RA - AF参数分析方法在此过程中被广泛采用。除了参数分析外，决策边界的可视化及支持向量的呈现，有助于更清晰地解读研究结果。下面，我们将使用Python来实现这一系列操作。

拉伸裂纹与剪切裂纹的识别

首先，我们需要加载必要的Python库。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC

假设我们已获取了一些声发射数据，并从中提取了RA（上升时间与幅值比率）和AF（平均频率）这两个特征参数，它们分别存储在ra_data和另一个数组中。同时，这些数据的标签（0代表拉伸裂纹，1代表剪切裂纹）则保存在另一个数组里。

af

data

labels

接下来，我们将RA和AF数据整合成一个二维数组，以便于后续处理。

# 假设的数据
ra_data = np.array([0.1, 0.3, 0.2, 0.5, 0.4, 0.6])
af_data = np.array([100, 200, 150, 300, 250, 350])
labels = np.array([0, 0, 1, 1, 0, 1])

data = np.column_stack((ra_data, af_data))

data

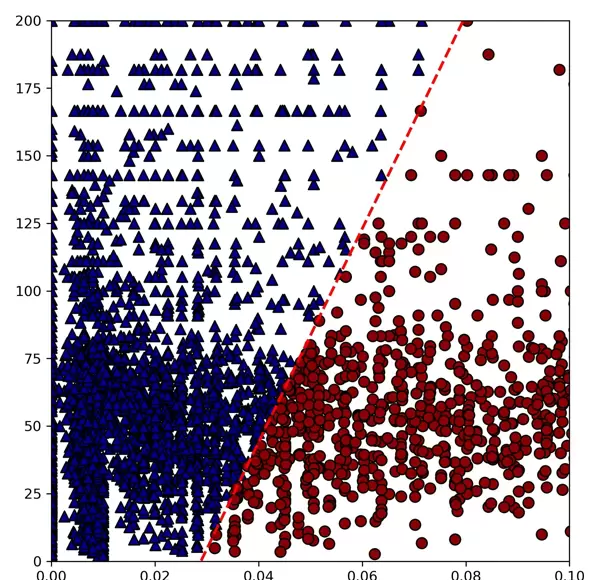
随后，通过支持向量机（SVM）算法对数据进行分类，以达到区分拉伸裂纹与剪切裂纹的目的。

svm_model = SVC(kernel='linear')
svm_model.fit(data, labels)

上述代码片段中，我们建立了一个线性核的支持向量机模型，并利用RA - AF数据集对其进行训练。训练完成后，该模型可用于预测未知数据点属于哪种类型的裂纹。

决策边界与支持向量的可视化

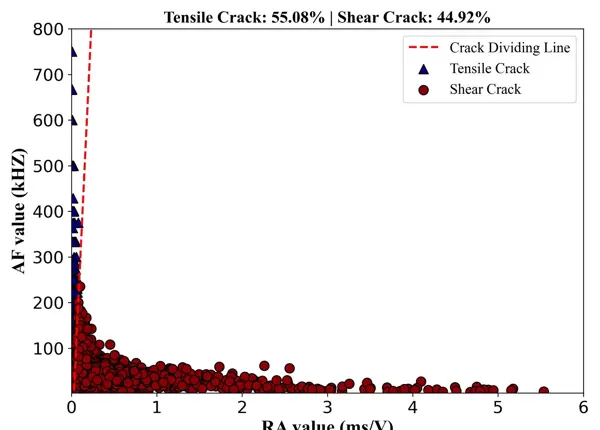
在完成模型训练之后，我们可以进一步对决策边界和支持向量进行可视化处理。

h =.02  # 网格步长
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = svm_model.predict(np.c_[xx.ravel(), yy.ravel()])

Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)

plt.scatter(data[:, 0], data[:, 1], c=labels, cmap=plt.cm.coolwarm)

# 绘制支持向量
sv = svm_model.support_vectors_
plt.scatter(sv[:, 0], sv[:, 1], s=100, facecolors='none', edgecolors='k')

plt.xlabel('RA Parameter')
plt.ylabel('AF Parameter')
plt.title('RA - AF Crack Mode Classification with Decision Boundary')
plt.show()

此部分代码首先设定了一个较小的网格间距，用于构建覆盖整个二维数据空间的网格。接着，利用np.meshgrid函数生成网格坐标。然后，应用训练好的SVM模型对网格中的每一个点进行分类预测，预测结果存储在一个变量中。

h

np.meshgrid

xx

yy

Z

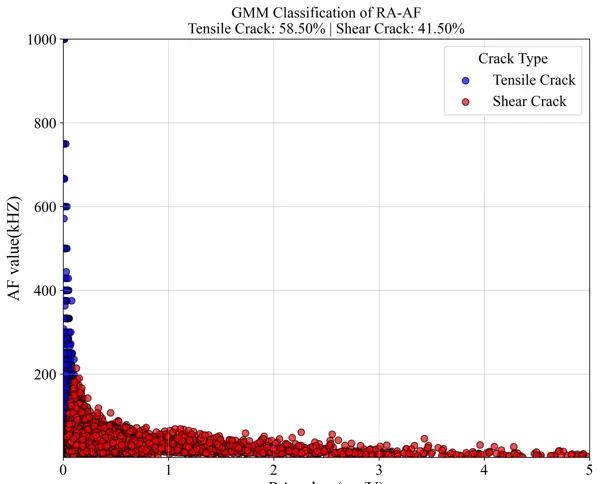
plot_decision_regions函数负责绘制决策边界，不同颜色的区域表示不同的预测结果。

plt.contourf

plt.scatter函数首先用来显示原始的数据点，点的颜色依据其对应的裂纹类型来决定。之后，同样使用plt.scatter来高亮显示支持向量，即那些对决策边界形成起关键作用的数据点。最后，我们为图表添加了坐标轴标签和标题，使其更加完整和易于理解。

plt.scatter

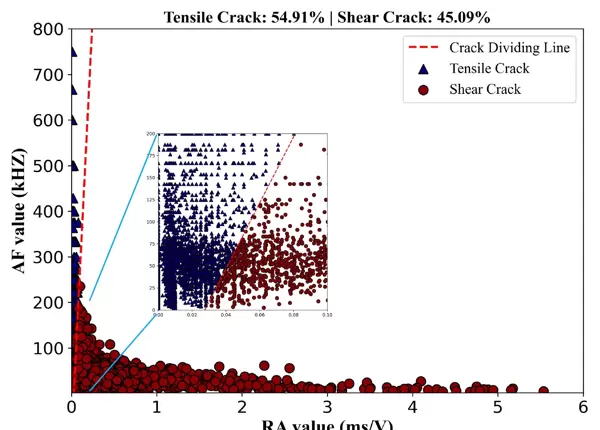
综上所述，借助Python编程语言及其相关库，我们不仅能够有效地区分拉伸裂纹与剪切裂纹，还能通过可视化技术直观展现决策边界和支持向量，从而为深入探讨材料裂纹特性提供了强有力的工具。