目录

序章：鸟群飞舞的启示

夕阳西下，成群的候鸟在天空中划出美丽的弧线。它们没有统一的指挥，却能默契地调整飞行方向，共同寻找温暖的栖息地。这种自然界中群体协作寻找目标的场景，正是粒子群优化算法（Particle Swarm Optimization, PSO）的灵感来源。

技术是桥梁，使计算机能够学会群体协作的智慧。在复杂的问题空间中寻找最优解时，PSO算法就像一群协同工作的智能体，通过个体经验与集体智慧的平衡，在广大的搜索空间中高效地找到那片“最优的栖息地”。

问题之源：优化困境与自然启示

生活中的优化难题

想象你在一片广阔的山丘中寻找最高点，但浓雾弥漫，视野受限。你只能依靠脚下坡度的感受和与同伴的沟通来做出决策。每个人既参考自己发现的最高位置的记忆，又关注群体中找到的最高点，通过这样的协作，整个群体能快速锁定目标。

这正是PSO要解决的核心问题：在高维、非线性、多峰值的复杂搜索空间中，如何高效地找到全局最优解。

传统优化方法的局限

传统的梯度下降法像一个人在浓雾中独自摸索，容易陷入局部最优的“小山坡”而错过真正的“最高峰”。遗传算法虽然引入了群体概念，但操作复杂，需要交叉、变异等生物进化机制。PSO的优雅之处在于其简洁性：仅通过位置和速度的更新，就能实现高效的全局搜索。

算法核心：群体智慧的数学表达

粒子群的基本概念

每个“粒子”代表一个潜在的解决方案，它们在搜索空间中飞行，通过两个关键因素调整自己的轨迹：个体认知（粒子自身找到的历史最优位置）和社会认知（整个群体找到的全局最优位置）。

数学原理的通俗解读

速度更新公式： 新速度 = 惯性 × 原速度 + 个体学习 × (个体最优 - 当前位置) + 社会学习 × (全局最优 - 当前位置)

用生活类比理解：
- 惯性项：保持原有飞行方向的“习惯势力”，避免急转弯。
- 个体认知项：基于个人经验的“怀旧情绪”，趋向自己找到的好位置。
- 社会认知项：向优秀同伴学习的“从众心理”，趋向群体找到的最佳位置。

位置更新公式： 新位置 = 原位置 + 新速度

这就像鸟群中每只鸟根据自己经验和群体信息，调整飞行方向和速度。

参数艺术：平衡探索与利用

关键参数的意义

惯性权重ω：平衡全局探索与局部开发
- ω较大：粒子飞行速度快，全局探索能力强
- ω较小：局部精细搜索，收敛精度高

学习因子c1、c2：平衡个体经验与群体智慧
- c1 > c2：粒子更相信自己的经验
- c2 > c1：粒子更倾向于跟随群体

参数调节的哲学

优秀的PSO调参如同指挥交响乐团，需要在探索（寻找新区域）和利用（精细搜索已知好区域）之间找到完美平衡。太强的探索可能导致收敛慢，太强的利用可能陷入局部最优。

实践落地：MATLAB实现与可视化

下面我们通过完整的MATLAB脚本来实现粒子群算法，并可视化优化过程。

%% 粒子群算法（PSO）MATLAB实现 - 多维函数优化
% 功能说明：本代码实现标准粒子群算法，用于求解多维函数最小值问题
% 以Rastrigin函数为例，展示PSO的优化过程和收敛特性
% 运行后将生成粒子运动轨迹动画和收敛曲线

clear; close all; clc;

%% 参数设置
n_particles = 30;      % 粒子数量
max_iter = 100;        % 最大迭代次数
dim = 2;               % 问题维度（2维便于可视化）

% PSO参数
w = 0.729;             % 惯性权重
c1 = 1.49445;          % 个体学习因子
c2 = 1.49445;          % 社会学习因子

% 搜索空间范围
x_min = -5.12;
x_max = 5.12;
v_max = (x_max - x_min) * 0.2;  % 速度限制

%% 初始化粒子群
% 位置初始化
positions = x_min + (x_max - x_min) * rand(n_particles, dim);
% 速度初始化
velocities = -v_max + 2 * v_max * rand(n_particles, dim);
% 个体最优位置
pbest_positions = positions;
% 个体最优适应度
pbest_values = inf(n_particles, 1);
% 全局最优位置和适应度
gbest_position = zeros(1, dim);
gbest_value = inf;

%% 初始化适应度计算
% 目标函数：Rastrigin函数（多峰值测试函数）
for i = 1:n_particles
    current_value = rastrigin(positions(i, :));
    
    % 更新个体最优
    if current_value < pbest_values(i)
        pbest_values(i) = current_value;
        pbest_positions(i, :) = positions(i, :);
    end
    
    % 更新全局最优
    if current_value < gbest_value
        gbest_value = current_value;
        gbest_position = positions(i, :);
    end
end

%% 记录收敛过程
convergence_curve = zeros(max_iter, 1);
particle_history = zeros(n_particles, dim, max_iter);

%% PSO主循环
figure('Position', [100, 100, 1200, 500]);
for iter = 1:max_iter
    % 记录当前粒子位置
    particle_history(:, :, iter) = positions;
    
    for i = 1:n_particles
        % 计算随机因子
        r1 = rand(1, dim);
        r2 = rand(1, dim);
        
        % 速度更新公式
        velocities(i, :) = w * velocities(i, :) + ...
                          c1 * r1 .* (pbest_positions(i, :) - positions(i, :)) + ...
                          c2 * r2 .* (gbest_position - positions(i, :));
        
        % 速度边界处理
        velocities(i, :) = max(min(velocities(i, :), v_max), -v_max);
        
        % 位置更新
        positions(i, :) = positions(i, :) + velocities(i, :);
        
        % 位置边界处理
        positions(i, :) = max(min(positions(i, :), x_max), x_min);
        
        % 计算新适应度
        current_value = rastrigin(positions(i, :));
        
        % 更新个体最优
        if current_value < pbest_values(i)
            pbest_values(i) = current_value;
            pbest_positions(i, :) = positions(i, :);
        end
    end
    
    % 更新全局最优
    for i = 1:n_particles
        if pbest_values(i) < gbest_value
            gbest_value = pbest_values(i);
            gbest_position = pbest_positions(i, :);
        end
    end
    
    % 记录收敛曲线
    convergence_curve(iter) = gbest_value;
    
    %% 实时可视化
    subplot(1, 2, 1);
    plot_optimization_process(positions, gbest_position, x_min, x_max, iter);
    
    subplot(1, 2, 2);
    semilogy(1:iter, convergence_curve(1:iter), 'b-', 'LineWidth', 2);
    xlabel('迭代次数');
    ylabel('最优适应度(对数尺度)');
    title('收敛曲线');
    grid on;
    
    drawnow;
    
    % 显示迭代信息
    fprintf('迭代 %d/%d, 最优值: %.6f\n', iter, max_iter, gbest_value);
    
    % 收敛判断
    if iter > 10 && abs(convergence_curve(iter) - convergence_curve(iter-1)) < 1e-6
        fprintf('算法已收敛于第 %d 代\n', iter);
        break;
    end
end

%% 最终结果展示
fprintf('\n=== 优化结果 ===\n');
fprintf('全局最优位置: [%.6f, %.6f]\n', gbest_position);
fprintf('全局最优值: %.6f\n', gbest_value);
fprintf('理论最优值: 0.000000\n');

%% 参数对比实验
figure('Position', [100, 100, 1000, 800]);
compare_parameters();

%% Rastrigin函数定义
function value = rastrigin(x)
    % Rastrigin函数：多峰值测试函数，全局最小值在原点，值为0
    % 公式：f(x) = 10n + Σ[x_i^2 - 10cos(2πx_i)]
    A = 10;
    n = length(x);
    value = A * n + sum(x.^2 - A * cos(2 * pi * x));
end

%% 优化过程可视化函数
function plot_optimization_process(positions, gbest, x_min, x_max, iter)
    % 绘制搜索空间和粒子位置
    [X, Y] = meshgrid(linspace(x_min, x_max, 100));
    Z = zeros(size(X));
    for i = 1:size(X, 1)
        for j = 1:size(X, 2)
            Z(i, j) = rastrigin([X(i, j), Y(i, j)]);
        end
    end
    
    contourf(X, Y, Z, 50, 'LineStyle', 'none');
    colormap(jet);
    colorbar;
    hold on;
    
    % 绘制粒子
    scatter(positions(:, 1), positions(:, 2), 40, 'white', 'filled', ...
            'MarkerEdgeColor', 'black', 'LineWidth', 1);
    
    % 标记全局最优
    scatter(gbest(1), gbest(2), 100, 'red', 'filled', 'pentagram', ...
            'MarkerEdgeColor', 'yellow', 'LineWidth', 2);
    
    hold off;
    title(sprintf('粒子群优化过程 (迭代: %d)', iter));
    xlabel('x1');
    ylabel('x2');
    axis([x_min, x_max, x_min, x_max]);
end

%% 参数对比函数
function compare_parameters()
    % 对比不同参数设置对PSO性能的影响
    
    test_cases = {
        {'高惯性权重', 0.9, 1.2, 1.2},    % w较大，探索性强
        {'低惯性权重', 0.4, 1.2, 1.2},    % w较小，开发性强  
        {'个体导向', 0.729, 2.0, 0.5},    % c1较大，重视个体经验
        {'社会导向', 0.729, 0.5, 2.0},    % c2较大，重视群体经验
        {'平衡参数', 0.729, 1.494, 1.494} % 标准参数
    };
    
    max_iter = 100;
    n_particles = 50;
    dim = 2;
    x_min = -5.12;
    x_max = 5.12;
    
    for case_idx = 1:length(test_cases)
        case_info = test_cases{case_idx};
        case_name = case_info{1};
        w = case_info{2};
        c1 = case_info{3};
        c2 = case_info{4};
        
        % 初始化
        positions = x_min + (x_max - x_min) * rand(n_particles, dim);
        velocities = zeros(n_particles, dim);
        pbest_positions = positions;
        pbest_values = inf(n_particles, 1);
        gbest_position = zeros(1, dim);
        gbest_value = inf;
        
        % 计算初始适应度
        for i = 1:n_particles
            current_value = rastrigin(positions(i, :));
            if current_value < pbest_values(i)
                pbest_values(i) = current_value;
                pbest_positions(i, :) = positions(i, :);
            end
            if current_value < gbest_value
                gbest_value = current_value;
                gbest_position = positions(i, :);
            end
        end
        
        convergence = zeros(max_iter, 1);
        
        % PSO迭代
        for iter = 1:max_iter
            for i = 1:n_particles
                r1 = rand(1, dim);
                r2 = rand(1, dim);
                
                velocities(i, :) = w * velocities(i, :) + ...
                                  c1 * r1 .* (pbest_positions(i, :) - positions(i, :)) + ...
                                  c2 * r2 .* (gbest_position - positions(i, :));
                
                velocities(i, :) = max(min(velocities(i, :), 1), -1);
                positions(i, :) = positions(i, :) + velocities(i, :);
                positions(i, :) = max(min(positions(i, :), x_max), x_min);
                
                current_value = rastrigin(positions(i, :));
                
                if current_value < pbest_values(i)
                    pbest_values(i) = current_value;
                    pbest_positions(i, :) = positions(i, :);
                end
            end
            
            % 更新全局最优
            for i = 1:n_particles
                if pbest_values(i) < gbest_value
                    gbest_value = pbest_values(i);
                    gbest_position = pbest_positions(i, :);
                end
            end
            
            convergence(iter) = gbest_value;
        end
        
        % 绘制收敛曲线
        subplot(2, 3, case_idx);
        semilogy(1:max_iter, convergence, 'LineWidth', 2);
        title(sprintf('%s\nw=%.3f, c1=%.3f, c2=%.3f', case_name, w, c1, c2));
        xlabel('迭代次数');
        ylabel('适应度');
        grid on;
    end
    
    sgtitle('不同PSO参数设置的性能对比');
end

运行说明：
- 将代码保存为

pso_optimization.m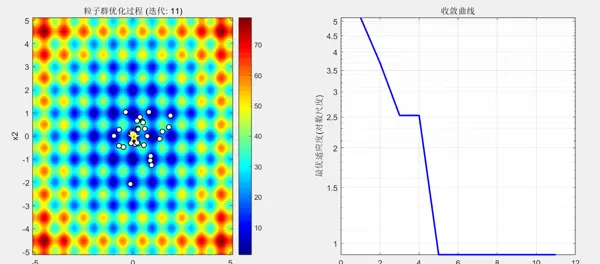

结果解读与技术价值

可视化结果的意义

粒子运动轨迹图： 白色圆点代表各个粒子在搜索空间中的位置；红色五角星标记当前找到的全局最优解；背景等高线显示目标函数的地形特征。从动画中可以观察到，粒子群最初随机分布，随后逐渐向全局最优点（原点附近）聚集，体现了群体智能的涌现行为。

收敛曲线： 显示算法随迭代次数增加，最优适应度持续下降，最终趋近于理论最优值0，验证了PSO的有效性。

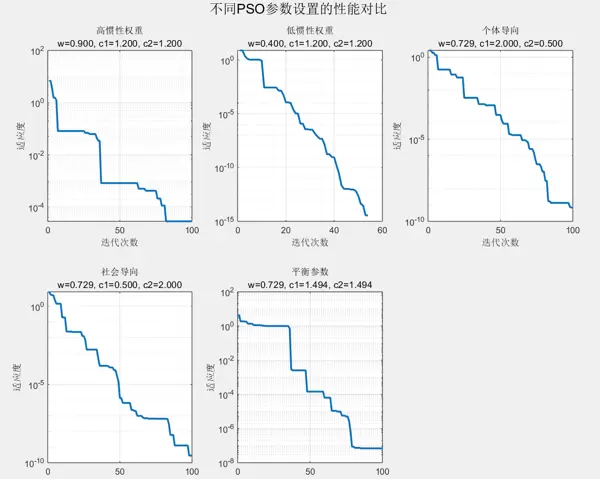
参数对比图： 揭示了不同参数设置对算法性能的影响：
- 高惯性权重收敛慢但探索能力强
- 低惯性权重收敛快但可能陷入局部最优
- 平衡的参数设置能在探索和开发间取得最佳平衡

应用场景与扩展思考

实际工程应用

PSO算法已成功应用于：
- 电力系统优化：机组组合、负荷分配
- 神经网络训练：权重优化，避免梯度消失
- 机器人路径规划：在多障碍环境中寻找最优路径
- 图像处理：图像分割参数优化

算法哲学思考

粒子群算法体现了个体与集体的辩证统一。每个粒子既保持个性（个体认知），又融入集体（社会认知），这种平衡正是算法成功的关键。如同人类社会的发展，个人创新与集体智慧的有机结合推动着文明进步。

结语：智能优化的诗意远方

从鸟群飞舞的自然现象到数学模型的精妙构建，粒子群算法向我们展示了简单规则如何涌现出复杂的智能。