作为深度学习的初学者，初次接触“线性回归”“Logistic 回归”“梯度下降”这些术语时，可能会觉得抽象难懂。但其实，它们背后的逻辑非常贴近生活——本质上不过是“画直线”“分水果”这类日常行为的数学表达。接下来，我会用通俗的生活类比，结合四个核心方法：线性回归、多项式回归、Logistic 回归和梯度下降，帮你理清思路，并能顺利跑通代码。

一、先搞清楚：两类任务，两种模型

在深入细节前，必须明确一个基本区分，避免后续概念混淆： - **回归问题**：目标是预测连续数值，例如根据房屋面积估算价格，或通过身高推测体重。这类问题通常使用「线性回归」和「多项式回归」来处理； - **分类问题**：目标是给数据打标签，比如判断一封邮件是否为垃圾邮件，或者区分苹果和橘子。这类任务中，「Logistic 回归」是一种专门用于二分类的经典方法。 明确了这一点后，我们从最基础的模型开始讲起。

二、线性回归：就像用尺子画一条最贴合点的直线

线性回归是许多机器学习模型的起点，它的思想很简单：找到一条直线，让它尽可能穿过所有数据点，实现最佳拟合。举个例子，如果我们想根据小朋友的身高预测体重，就可以借助这种方法。

1. 生活案例：从身高推测体重

假设我们收集了三个孩子的数据： | 身高（cm） | 体重（kg） | |------------|-----------| | 120 | 25 | | 130 | 30 | | 140 | 35 | 现在有一个新孩子，身高125cm，该怎么估计他的体重？我们可以尝试画一条“最贴合已有数据”的直线来进行预测。

2. 实现步骤：三步走策略

第一步：把数据可视化（画在纸上）
拿出一张坐标纸，横轴表示身高（x），纵轴表示体重（y），将上述三组数据标成散点。这一步的作用是直观观察数据分布趋势，在代码中对应如下操作：

plt.plot(x_train, y_train, 'bo')

第二步：先随意画一条直线（初始化模型）
一开始我们并不知道最优直线是什么样子，所以可以先“猜”一条。比如假设直线方程为：

y = 0.5x - 35

其中

x

表示身高，

y

是预测的体重。 代入计算： - 当身高为120cm时，预测体重 =

0.5×120 - 35 = 25kg

（与真实值一致）； - 130cm →

0.5×130 - 35 = 30kg

（也正确）； - 140cm →

0.5×140 - 35 = 35kg

（完全吻合！） 这种情况属于“完美拟合”，但在现实中几乎不可能一次猜准。更常见的是我们初始猜测为：

y = 0.4x - 20

此时： - 120cm 预测结果为

0.4×120 - 20 = 28kg

，而实际是25kg，差了3kg。 这种“预测值与真实值之间的差异”就是所谓的「误差」。在程序中，通常使用如下函数来衡量误差大小：

get_loss

其公式为“预测值减去真实值的平方再求平均”，即均方误差（MSE）。误差越小，说明直线越贴近真实数据。 第三步：不断调整直线以减小误差（梯度下降）
如果当前直线误差较大，该如何优化？这就引入了「梯度下降」算法——可以理解为沿着误差下降的方向微调直线参数。 例如： - 如果发现所有预测值都偏高，就把直线整体下移； - 若普遍偏低，则上移； - 每次移动的“步长”称为「学习率」（如0.01），它不能太大（否则会震荡不收敛），也不能太小（收敛速度极慢）。 在代码中的关键流程如下（简化版）：

# 1. 导入工具包
import torch
import numpy as np
import matplotlib.pyplot as plt

# 2. 准备真实数据（身高-体重）
x_train = np.array([[120], [130], [140]], dtype=np.float32)  # 身高
y_train = np.array([[25], [30], [35]], dtype=np.float32)  # 体重
# 转成PyTorch能处理的Tensor
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)

# 3. 定义初始直线（w是斜率，b是截距）
w = torch.randn(1, requires_grad=True)  # 初始随机斜率
b = torch.zeros(1, requires_grad=True)   # 初始截距0

# 4. 直线公式（模型）
def linear_model(x):
    return x * w + b

# 5. 计算误差（误差越小越好）
def get_loss(y_pred, y_true):
    return torch.mean((y_pred - y_true) ** 2)

# 6. 重复调整10次（梯度下降）
for e in range(10):
    # 用模型预测体重
    y_pred = linear_model(x_train)
    # 算误差
    loss = get_loss(y_pred, y_train)
    # 清空之前的调整记录
    if w.grad is not None:
        w.grad.zero_()
    if b.grad is not None:
        b.grad.zero_()
    # 自动算“该怎么调”（梯度）
    loss.backward()
    # 按梯度调整w和b（学习率0.00003）
    w.data = w.data - 0.00003 * w.grad.data
    b.data = b.data - 0.00003 * b.grad.data
    # 打印每次调整的误差
    print(f"第{e+1}次调整，误差：{loss.data:.4f}")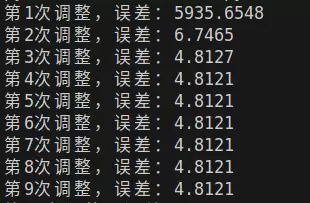

关于学习率的选择建议： - 误差逐渐趋近于0 → 学习率合适； - 误差上下剧烈波动 → 学习率过大； - 误差几乎不变 → 学习率过小。 运行这段代码可以看到：误差从几千逐步下降到接近零——这意味着模型正在一点点逼近最优解。 第四步：利用训练好的直线做预测
当误差足够小时，假设最终得到的直线是：

y = 0.5x - 35

那么对于身高125cm的孩子，代入公式得：

0.5×125 - 35 = 27.5kg

这就是线性回归的核心目的：建立一个能泛化到新数据的预测模型。

三、多项式回归：让直线变曲线，应对更复杂的关系

线性回归只适用于数据呈线性分布的情况。然而现实中有许多非线性关系，例如“学习时间”与“考试分数”之间并非匀速增长：刚开始每多学一小时提升明显，但学到一定程度后进步越来越慢。 这时就需要「多项式回归」出场了——它通过增加高阶项，把直线变成曲线，从而更好地拟合弯曲的数据模式。

1. 生活场景：学习时间与考试成绩的关系

设想目标函数是一条S型曲线：

y = 0.9 + 0.5x + 3x? + 2.4x?

其中 x 代表学习时间，y 是得分。数据呈现出“先缓慢上升，随后加速，最后趋于平缓”的趋势。显然，一条直线无法有效拟合这样的分布，必须改用曲线。

2. 核心原理：给线性公式加“弯曲项”

多项式回归的本质是在原始线性公式：

y = wx + b

的基础上加入更高次幂的项，如 x、x 等，使模型具备弯曲能力。 常见的形式包括： - 二次多项式：

y = w1x + w2x? + b

（形成抛物线）； - 三次多项式：

y = w1x + w2x? + w3x? + b

（可拟合更复杂的波浪形）。 在代码中定义此类模型的方式如下：

# 导入工具包
import torch
import numpy as np
import matplotlib.pyplot as plt


# 准备数据：x是学习时间，x_train包含x、x?、x?（高次项）
x_sample = np.arange(-3, 3.1, 0.1)  # 学习时间范围
# 构建特征：[x, x?, x?]（给模型提供“弯曲”的依据）
x_train = np.stack([x_sample ** i for i in range(1, 4)], axis=1)
x_train = torch.from_numpy(x_train).float()
# 真实分数（用目标曲线生成）
y_true = 0.9 + 0.5*x_sample + 3*x_sample**2 + 2.4*x_sample**3
y_true = torch.from_numpy(y_true).float().unsqueeze(1)

# 定义三次多项式模型（w有3个参数，对应x、x?、x?的权重）
w = torch.randn(3, 1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)

def poly_model(x):
    # 模型：y = w1x + w2x? + w3x? + b
    return torch.mm(x, w) + b

def get_loss(y_pred, y_true):
    # 均方误差：衡量预测曲线和真实曲线的差距（和线性回归逻辑一样）
    return torch.mean((y_pred - y_true) ** 2)

# 6. 重复调整20次（梯度下降）
for e in range(20):
    # 用模型预测体重
    y_pred = poly_model(x_train)
    # 算误差
    loss = get_loss(y_pred, y_true)
    # 清空之前的调整记录
    if w.grad is not None:
        w.grad.zero_()
    if b.grad is not None:
        b.grad.zero_()
    # 自动算“该怎么调”（梯度）
    loss.backward()
    # 按梯度调整w和b（学习率0.00003）
    w.data = w.data - 0.005 * w.grad.data
    b.data = b.data - 0.005* b.grad.data
    # 打印每次调整的误差
    print(f"第{e+1}次调整，误差：{loss.data:.4f}")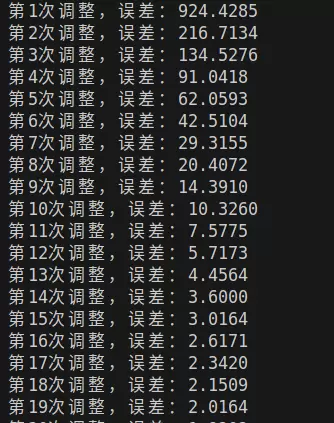

运行后你会发现：初始阶段误差较大，曲线偏离严重；但经过约20轮调整后，预测曲线与真实分布几乎重合。这正是多项式回归的优势所在——能够捕捉非线性规律。

四、Logistic 回归：像用粉笔划线分水果，解决分类问题

前面提到的线性与多项式回归主要用于数值预测，而 Logistic 回归则专注于“分类”任务。比如帮助水果摊阿姨区分苹果和橘子，关键是找到一条“决策边界”，将两类样本分开。

1. 生活场景：依据颜色和甜度判断水果种类

假设我们有两种水果：苹果偏红且较甜，橘子偏橙且略酸。我们采集了一批样本，每个样本有两个特征：颜色深浅和甜度值。目标是建立一个规则，自动判断新来的水果是哪一类。 这个问题就属于典型的二分类任务，适合使用 Logistic 回归建模。

2. 基本思路：寻找分割两类的“分界线”

Logistic 回归并不是真的做“回归”，而是利用类似回归的方式输出一个介于0到1之间的概率值，再设定阈值（如0.5）进行分类。 例如： - 输出0.8 → 判定为苹果； - 输出0.2 → 判定为橘子。 这个过程就像是在二维平面上画一条线（或曲面），使得苹果集中在一侧，橘子在另一侧。虽然内部计算涉及sigmoid函数和对数似然，但从功能上看，它就是在“找一条最好的分界线”。 尽管没有显式的图像标记在此部分，但若原内容有相关图示位置，应按顺序保留并标注，例如后续若有图形插入需求，应保持结构一致性。

假设有一个水果篮，里面有4个水果，每个水果都有两个特征：颜色深浅（0-10）和甜度（0-10）。标签表示水果类别：“苹果 = 1”，“橘子 = 0”：

• 颜色深浅：8，甜度：7，标签：1
• 颜色深浅：9，甜度：8，标签：1
• 颜色深浅：3，甜度：4，标签：0
• 颜色深浅：2，甜度：3，标签：0

现在出现一个新水果，颜色为6，甜度为5。如何判断它是苹果还是橘子？解决方法是引入一条“分界线”来进行分类。

核心思路：三步确定最优分界线

第一步：使用 Sigmoid 函数将输出转化为概率

在分类任务中，我们更关注“可能性”而非绝对判断。例如，“有80%的概率是苹果”比“一定是苹果”更具灵活性。Sigmoid 函数的作用正是将任意数值映射到0到1之间，适合作为概率输出。

规则如下：

• 若输出 ≥ 0.5，则判定为类别1（苹果）；
• 若输出 < 0.5，则判定为类别0（橘子）。

Sigmoid 函数的形态如下（无需记忆公式，理解其功能即可）：

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

第二步：设定初始分界线（即初始模型）

首先可以随意画一条直线作为初步的分类边界。例如：

颜色 + 甜度 = 10

设定规则：

• 直线上方（颜色 + 甜度 > 10）→ 判定为苹果；
• 直线下方（颜色 + 甜度 < 10）→ 判定为橘子。

在此情况下，原始的4个样本全部被正确分类。但在实际应用中，初始分界线往往不够准确。比如如果分界线画成这样：

颜色 + 甜度 = 15

所有样本都落在下方区域，会被统一归类为橘子，导致较大的分类误差。

第三步：通过梯度下降优化分界线，减少错误

与回归问题不同，分类任务采用“对数损失”来衡量误差——分对时损失小，分错时损失大。该过程对应代码中的关键步骤：

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 1. 导入PyTorch工具（用优化器自动调整参数）
import torch
import numpy as np
import torch.nn.functional as F
from torch import nn
from torch.optim import SGD


# 2. 准备数据（颜色、甜度、标签）
data = [(8,7,1), (9,8,1), (3,4,0), (2,3,0)]
np_data = np.array(data, dtype=np.float32)
x_train = torch.from_numpy(np_data[:, 0:2])  # 特征：颜色、甜度
y_train = torch.from_numpy(np_data[:, -1]).unsqueeze(1)  # 标签：0或1



# 3. 定义模型（线性分界线 + Sigmoid概率）
w = nn.Parameter(torch.randn(2, 1))  # 2个参数：颜色权重、甜度权重
b = nn.Parameter(torch.zeros(1))

def logistic_model(x):
    # 先算线性分界线，再用Sigmoid转成概率
    return F.sigmoid(torch.mm(x, w) + b)

# 4. 分类误差计算（对数损失）
def binary_loss(y_pred, y_true):
    # 防止log(0)出错，用clamp限制范围
    y_pred = y_pred.clamp(1e-12, 1 - 1e-12)
    return -torch.mean(y_true * torch.log(y_pred) + (1 - y_true) * torch.log(1 - y_pred))

# 5. 用优化器自动调整（比手动调更方便）
optimizer = SGD([w, b], lr=0.1)  # 学习率0.1

# 6. 重复调整1000次（分类需要更多迭代）
for e in range(1000):
    # 预测概率
    y_pred = logistic_model(x_train)
    # 算误差
    loss = binary_loss(y_pred, y_train)
    # 清空之前的调整记录
    optimizer.zero_grad()
    # 自动算梯度
    loss.backward()
    # 自动调整参数
    optimizer.step()
    # 每200次看一次正确率
    if (e + 1) % 200 == 0:
        # 概率≥0.5算1类，否则0类
        mask = y_pred.ge(0.5).float()
        # 正确率=对的数量/总数量
        acc = (mask == y_train).sum().data / y_train.shape[0]
        print(f"第{e+1}次调整，误差：{loss.data:.5f}，正确率：{acc:.5f}")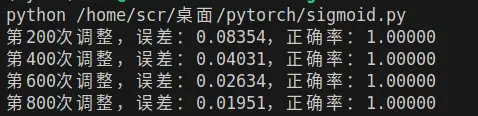

运行程序后可观察到，模型的正确率逐步上升，最终达到100%。这意味着分界线不断调整，逐渐逼近最佳位置，成功将苹果和橘子完全区分开。

第四步：利用训练好的模型判断新样本

对于新水果（颜色6，甜度5），将其代入已训练的模型进行预测：

• 若输出概率为0.8 → 表示80%可能是苹果，判定为类别1；
• 若输出概率为0.2 → 表示80%可能是橘子，判定为类别0。

核心总结：四种关键模型/算法对比

模型/算法	解决的问题	核心逻辑
线性回归	预测连续值（如体重、房价）	拟合一条直线贴近数据点，用以预测新样本
多项式回归	处理非线性分布的连续值预测	引入高次项（如x、x），使直线变为曲线，更好地贴合复杂数据
Logistic 回归	二分类问题（如苹果/橘子、0/1）	通过画分界线分离两类样本，并结合 Sigmoid 函数计算归属概率
梯度下降	优化各类模型的参数	从随机初始值开始，根据误差不断微调参数，直至误差最小化

实践建议

1. 先运行线性回归代码：观察误差随迭代逐步减小的过程，直观感受“模型学习”的机制；
2. 再尝试多项式回归：比较直线与曲线的拟合效果，深入理解高次项在捕捉非线性关系中的作用；
3. 最后实践 Logistic 回归：关注分类正确率的变化，体会“分界线”是如何一步步调整至最优状态的；
4. 避免死记硬背公式：优先掌握背后的“生活化逻辑”，再与代码中的函数相对应。例如，“计算误差”对应的是：

get_loss

而“调整参数”的过程则体现在以下图示中：

loss.backward()

optimizer.step()

深度学习的真正入门门槛，并不在于复杂的数学推导，而在于能否将抽象的算法逻辑与现实生活场景建立联系。