一、复变函数在某点可导性的极限判定方法

在实变函数中，判断一个函数在某点是否可导，通常只需考察该点左右两侧的极限是否存在且相等。由于变量仅沿实轴（x轴）方向变化，逼近路径唯一，因此只要左极限等于右极限，并满足连续性条件，即可断定可导。

然而，在复变函数中，自变量是复数 $ z = x + iy $，其趋近于某点 $ z_0 $ 的方式是二维平面上任意路径的逼近——可以沿实轴、虚轴，也可以沿任意斜线甚至曲线接近。因此，复变函数在某点可导的前提是：无论从哪个方向逼近该点，极限值都必须相同。

为了验证这一点，常用的方法是设定逼近路径为 $ y - y_0 = k(x - x_0) $，即令 $ \Delta y = k\Delta x $，代入导数的极限定义式中进行化简。若最终结果与参数 $ k $ 无关，则说明所有方向的极限一致，函数在该点可导；反之，若结果仍含有 $ k $，则表明不同方向的极限不一致，函数在该点不可导。

实践中，这种方法更多用于证明某点不可导，而非可导。

二、解析函数及其判别准则

（1）解析性的定义：邻域内处处可导

一个复变函数在某点“解析”，意味着它不仅在该点可导，而且在该点的某个邻域内每一点都可导。换句话说，解析性比单纯某点可导更强，要求局部范围内整体可导。

（2）柯西-黎曼方程：可导的充要条件

虽然理论上需验证所有路径极限的一致性来判断可导性，但实际操作困难。于是我们转而考虑两个特殊方向的偏导数：沿实轴和虚轴方向的逼近。

设复变函数 $ f(z) = u(x, y) + iv(x, y) $，其中 $ z = x + iy $，$ u $ 和 $ v $ 分别为实部和虚部函数。当函数在某点可导时，其实部和虚部的偏导数需满足以下关系：

$$ \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x} $$

这组等式称为柯西-黎曼方程（Cauchy-Riemann equations）。它是复变函数在某点可导的必要条件。也就是说，如果函数在某点可导，那么必定满足该方程；反过来，若不满足，则一定不可导。

进一步地，在适当的光滑性条件下（如偏导数连续），柯西-黎曼方程也是充分条件。因此对于工程数学应用而言，可以直接将其视为可导的充要条件使用。

此外，由于可导意味着所有方向极限相同，因此求导时可任选一种简便路径计算，例如直接利用对 $ x $ 的偏导或结合虚部对 $ y $ 的偏导得出导数值。

三、初等函数在复数域中的推广与特性分析

掌握柯西-黎曼方程后，我们可以将其应用于常见初等函数，分析它们在复平面上的可导性、多值性及其他性质，为后续学习提供基础工具支持。

（1）指数函数

复指数函数是所有复初等函数中最重要且形式最优雅的一个，必须熟练掌握。

关于复指数函数的主要特性总结如下：

• 任意复数均可通过欧拉公式表示为指数形式 $ re^{i\theta} $，这种形式本质上是一个旋转缩放变换器。
• 实部控制缩放比例，虚部决定旋转角度；周期性体现在 $ e^{z + 2k\pi i} = e^z $，即每隔 $ 2\pi i $ 重复一次。
• 函数 $ f(z) = e^z $ 在整个复平面满足柯西-黎曼方程，因而处处可导、处处解析。
• 其导数仍为 $ e^z $，与实变函数情形一致。
• 每个输入 $ z $ 对应唯一的输出值，故为单值函数。

（2）对数函数

在复变函数中，为区分普通对数，常将复对数记作大写形式（如 $ \text{Ln}\,z $），以强调其多值性特征。

复对数函数的基本性质包括：

• 它是多值函数，因为幅角 $ \arg z $ 可加任意 $ 2k\pi $（$ k \in \mathbb{Z} $），导致同一个 $ z $ 对应无穷多个对数值。
• 通常取主值分支（主幅角 $ -\pi < \theta \leq \pi $）进行分析。
• 仍然保留 $ 2k\pi i $ 的周期结构，与指数函数互为反函数关系。
• 求导规则与实函数相同：$ (\text{Ln}\,z)' = 1/z $。

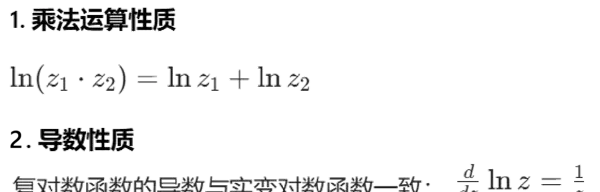
（3）幂函数

复幂函数的形式为 $ z^\alpha $，其中底数 $ z $ 是变量，指数 $ \alpha $ 为复常数。其定义依赖于对数函数：

$$ z^\alpha = e^{\alpha \ln z} $$

由此可见，幂函数实际上是通过对数再取指数的方式构造而成，属于复合函数结构。

关键特性如下：

• 由于依赖于对数函数 $ \ln z $，而后者为多值函数，因此 $ z^\alpha $ 一般也为多值函数。
• 分析方法与对数函数类似，需注意分支选取问题。

（4）三角函数

复三角函数可通过指数函数线性组合定义，例如：

$$ \sin z = \frac{e^{iz} - e^{-iz}}{2i}, \quad \cos z = \frac{e^{iz} + e^{-iz}}{2} $$

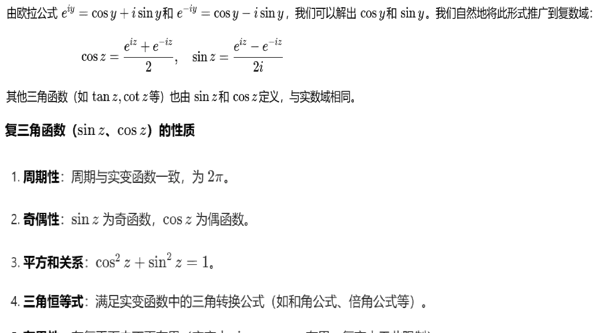
主要特点归纳如下：

• 本质是指数函数的代数组合，因此许多性质可由指数函数推导而来。
• 不再具有有界性：例如 $ |\sin z| $ 和 $ |\cos z| $ 在复平面上可以趋于无穷大。
• 其余代数性质（如周期性、恒等式等）与实数域下保持一致。

（5）规律总结

面对复变函数中各类初等函数复杂多样的行为，为便于理解和记忆，特总结如下通用规律：

• 每一类复初等函数在其对应的实变函数基础上，引入了新的特性，如多值性、无界性、周期性增强或几何解释深化（如旋转缩放）。
• 这些新增特性大多源于复数本身的二维结构以及幅角的多值本质。
• 大多数函数的求导规则仍延续实变函数形式，便于工程应用中的快速迁移。

在复变函数中，许多原本在实数域中不具备周期性的函数引入了虚周期性。例如，指数函数和对数函数在复平面上表现出周期性特征，其周期为2Kπi；对数函数还具有多值性，这是由于复数幅角的不确定性所导致的。三角函数虽然在实数域中已有周期性，但在复数域中失去了有界性，呈现出无界的特点。幂函数由对数函数衍生而来，因此也继承了多值性；至于其周期性，则需根据具体情况进行分析，较为复杂。

关于解析域的问题，复变函数的解析范围通常与对应实变函数的定义域相对应。指数函数在实数域中的定义域为x∈（-∞，+∞），将其推广到复平面后，即以z代替x，该函数在整个复平面上解析。对数函数在实数域中定义于x∈（0，+∞），推广至复数域后，其解析区域为除去原点及负实轴的整个复平面（尽管从实数定义域推导，似乎第二、三象限都应排除，但此处作为特例记忆即可）。幂函数因基于对数函数构建，故其解析域与对数函数一致。三角函数在实数域中定义域为全体实数，在复数域中同样在整个复平面上解析。

周期性的变化是复变函数的重要特性之一：原本在实数域中不具周期性的函数，在复数域中获得了虚周期2Kπi；而原本具有周期性的三角函数等，则保留了实数域中的周期规律。然而，幂函数作为指数与对数的复合形式，其周期性表现更为复杂，目前尚无统一简洁的总结方式，需具体情况具体分析。

此外，复变函数延续了实变函数的诸多运算规则。诸如求导法则、四则运算以及各类恒等式等，在复数域中依然成立，且形式保持不变。这使得许多在实数范围内适用的数学工具可以顺利推广至复数情形。