技术实践观察地址：Calculator Game

摘要：

24点等数字计算类游戏是计算机科学中一个经典问题，对回溯搜索（Backtracking）算法、表达式解析器（Parser）设计以及浮点数精度控制提出了较高要求。本文深入探讨如何通过回溯法实现所有可能运算路径的完整遍历，分析在表达式求值过程中如何借助中缀转后缀（RPN）机制高效处理括号优先级，并解决除法操作中的整除性判断与浮点误差问题。

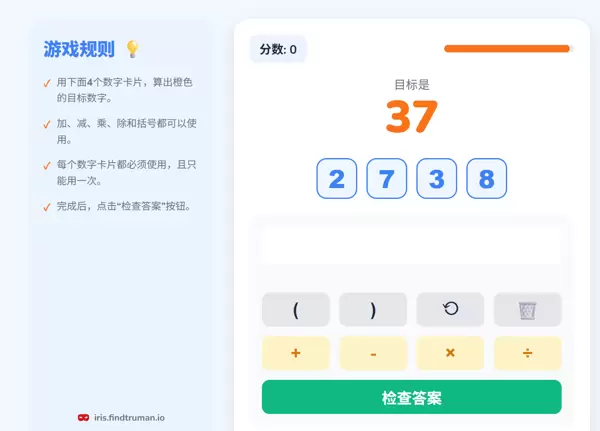
一、24点问题的算法完备性挑战

24点游戏规则限定使用4个数字，每个数字必须且仅能使用一次，这使得解空间虽有限但规模庞大。构建高效求解器的核心难点在于确保算法具备完备性（Completeness）——即：若有解则必能找到；若无解则可明确判定。

为实现这一目标，需穷尽以下三方面组合：

• 数字排列（Permutations）：4个不同数字共有 $4! = 24$ 种排列方式。
• 运算符组合（Combinations）：三次运算每次可选加、减、乘、除四种操作，共 $4^3 = 64$ 种组合。
• 运算结构（括号顺序）：不同的括号嵌套对应不同的运算优先级，其基本结构数量由卡特兰数决定，$C_3 = 5$ 种。

因此，总的运算序列组合数为 $24 \times 64 \times 5 = 7680$，均需被系统化地搜索与验证。

二、核心技术实现：回溯搜索与表达式解析

高效的24点求解通常基于状态空间上的回溯搜索框架，结合递归策略统一处理数字顺序与运算结构。

基于递归的回溯搜索机制

状态定义：当前剩余可用数字的集合 $S$。

回溯流程：递归函数接收集合 $S$，从中任取两个数 $a$ 和 $b$，执行四则运算（+、、×、÷），将结果 $r$ 与剩余数字 $S \setminus \{a, b\}$ 构成新集合 $S'$，递归进入下一层。

终止条件：当集合中仅剩一个数值时，判断其是否接近目标值（如24）。若满足条件，则当前路径对应的表达式即为有效解。

该方法巧妙融合了数字排列与括号结构的枚举，避免显式构造所有括号形式。

表达式解析与求值：从中缀到后缀

用户输入通常为人类易读的中缀表达式（例如：(3 + 5) × 3），而计算机更适合处理无括号的后缀表达式（Postfix / RPN）。

解析器设计：内置基于调度场算法（Shunting-Yard Algorithm）的解析模块。该算法利用运算符栈，动态管理优先级和括号层级，将中缀表达式准确转换为RPN序列。

求值优化：RPN表达式可通过单一操作数栈完成求值，逻辑简洁、效率高，适用于实时输入校验场景。

(8 * (7 - 2)) - 3

浮点数精度与整除性控制

除法引入两大关键问题：

• 整除性剪枝：部分24点变种要求中间结果必须为整数。求解器可在每次除法后加入整除判断，剔除非整路径，显著减少无效搜索。
• 浮点误差容忍：由于浮点运算存在精度损失，在判断最终结果 $Result$ 是否等于目标值 $T$ 时，应采用容差比较：$|Result - T| < \epsilon$，而非直接使用等号判断。

Result == T

三、应用场景与技术价值体现

将复杂的回溯逻辑与高性能表达式解析集成至直观的Web界面，极大增强了工具的实用性与教学意义。

以名为Calculator Game的Web应用为例，其提供按钮式输入与“检查答案”功能，背后依托严谨的算法引擎支撑。该类工具的价值体现在：

• 验证解的存在性：快速判断任意给定数字组合是否存在合法解。
• 展示工程级解析能力：用户在输入表达式时，实质上正与一个基于调度场算法的工业级解析器进行交互。

四、总结与未来展望

数字计算游戏的自动求解是对基础算法能力的综合考验。通过结合回溯搜索保障解空间的完整性，运用RPN转换提升表达式求值效率，并细致处理浮点精度与整除约束，可构建出兼具准确性与性能的求解系统。

此类工具不仅具有娱乐属性，更为学习者理解组合优化、递归搜索、栈的应用等核心算法思想提供了直观的学习平台，具备良好的教育拓展潜力。