Allan方差这个工具，怎么把它用的更顺手？（附Allan方差、动态Allan方差代码）

234

收藏 2025-11-26

前言

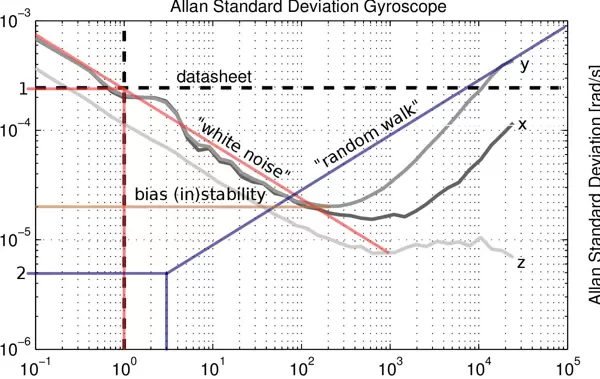
Allan方差由美国国家标准局的David Allan在20世纪60年代提出，最初用于分析振荡器的频率稳定性。该方法具备良好的统计特性辨识能力，能够有效区分多种误差源。在惯性器件领域，Allan方差被广泛应用于陀螺仪的噪声分析，可识别五类典型误差：量化噪声、角度随机游走（角速率白噪声）、零偏不稳定性、角速率随机游走（角加速度白噪声）以及速率斜坡（角速率趋势项）。

一、Allan方差的基本原理

假设以固定采样间隔 τ 对陀螺输出的角速率数据进行采集，共获得 N 个样本点。将这些数据划分为 K 组，每组包含 m 个连续采样值，即：

ω, ω, ..., ω （第1组），...，ω_Nm+1, ω_Nm+2, ..., ω_N （第K组）

此时，相关时间定义为 τ = mτ。每一组的平均角速率可表示为：

Ω_k = (1/m) Σ^m_i=1 ω_(k1)m+i，其中 k = 1, 2, ..., K

经典Allan方差的表达式如下：

σ_A(τ) = 1/[2(K1)] Σ^K1_k=1 (Ω_k+1 Ω_k)

其中符号表示总体均值操作。通过改变相关时间 τ 的大小，可以获得不同尺度下的方差估计，进而绘制出 σ_A(τ) 随 τ 变化的曲线，其双对数坐标图即为Allan方差图。

从理论角度看，Allan方差是一种基于时域的随机过程分析工具。但由于实际中只能获取有限长度的数据序列，因此该方法本质上是对真实方差的一种估计，具有一定的统计偏差。研究指出，Allan标准差估计值 σ_A(τ) 的相对均方误差可近似为：

E_A(τ) = |σ_A(τ) σ_A(τ)| / σ_A(τ) ≈ 1/√[2(N/m 1)] × 100%

其中 N 为总采样数，N/m 即为分组数量。由此可见，当分组数减少时，估计误差增大，因此需在分辨率与精度之间权衡。

二、动态Allan方差的核心思想

传统Allan方差适用于平稳信号的分析，但在实际应用中，陀螺信号常因环境扰动而表现出非平稳特性，其误差成分可能随时间发生显著变化。为此，动态Allan方差（DAVAR）被提出以应对这一挑战。

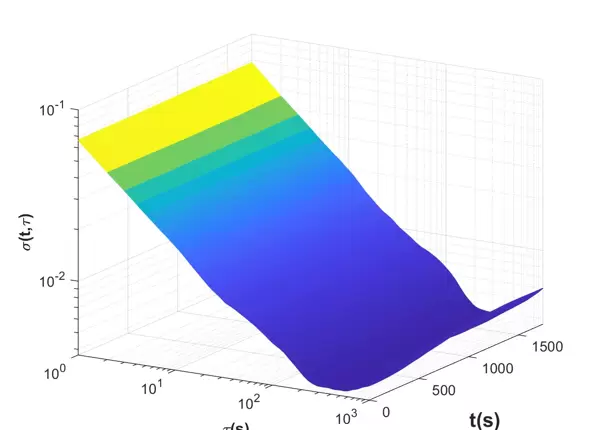
其核心思路是：将整个信号分割为多个时间窗口，在每个窗口内独立计算Allan方差，最终将所有结果整合成一个三维图谱——两个横轴分别为时间与相关时间 τ，纵轴为方差值。这样不仅保留了传统Allan分析的多尺度特性，还引入了时间维度，使误差行为的时变特征得以可视化呈现。

三、快速DAVAR的实现原理

3.1 递归算法设计

为了提升计算效率，快速DAVAR采用递归方式更新各时间段内的均值和方差，避免重复遍历数据。通过对前一状态的结果进行迭代修正，大幅降低运算复杂度，特别适合处理长序列数据。

3.2 相关时间选择策略

在计算过程中，并非所有相关时间都需要参与运算。通常选取满足 τ = n×τ 的离散值集合，且遵循对数分布规律（如每倍频程取若干点），以保证在宽时间范围内有足够分辨率的同时控制计算量。

四、关键代码结构解析

4.1 快速动态Allan方差主函数

主函数负责整体流程调度：读取输入数据、划分滑动时间窗、调用子函数完成局部Allan方差计算，并组织输出三维结果矩阵。通过设置步长与窗口长度参数，实现时间-尺度-方差的立体映射。

4.2 子函数1：局部Allan方差计算模块

该模块针对某一时间窗口内的数据执行标准Allan方差运算。输入为一段角速率序列，输出为其在多个相关时间下的方差值。内部实现包括数据分组、均值序列生成及差分平方求和等步骤。

4.3 子函数2：递归均值与方差更新单元

用于支持高效滑动窗口处理。利用递推公式动态维护当前窗口的统计量，减少冗余计算，提高整体运行速度，尤其适用于实时或近实时分析场景。

总结

Allan方差作为惯性传感器误差建模的重要工具，能够有效分离多种噪声类型。而动态Allan方差进一步拓展了其适用范围，使其可用于非平稳信号分析。结合快速算法与合理的时间尺度选择策略，可在保证精度的前提下显著提升计算效率，适用于工程实践中对长时间运行陀螺性能的监测与评估。

以光纤陀螺为例，其输出通常表现为角增量形式。因此，Allan方差可采用角增量的形式进行表达：

σ_A²(τ) = (1/2)(Ω_k+m Ω_k)² = 1/(2mτ) × 1/(N2m) × ∑_n=0^N2m1 [θ[n+2m] 2θ[n+m] + θ[n]]

其中，θ[n] 表示在第 n 个时刻所测得的角度值。

DAVAR（动态Allan方差）的定义如下：针对具有时变特性的随机信号 θ(t)，可在不同时间段内重复估计其Allan方差。具体而言，在时间点 t 处，利用长度为 N_w 的矩形窗对信号 θ(t) 进行截断，并计算该片段的Allan方差。通过在每个时间点 t 上执行相同操作，并汇总所有区间内的Allan方差结果，即可获得完整的DAVAR表示。

Allan方差通过绘制 σ_A²(τ) 与相关时间 τ 的二维关系曲线来描述信号的误差特性；而DAVAR则引入时间维度 t，构建出一个关于时间 t 和相关时间 τ 的三维图形，从而反映随机信号误差随时间演变的特征。因此，DAVAR可被定义为一组随时间变化的Allan方差曲线簇：

σ_A²[n, m] = 1/(2mτ) × 1/(N_w2m) × ∑_{k = nN_w/2}^n+N_w/22m1 [θ[k+2m] 2θ[k+m] + θ[k]]

式中，N_w 表示所选滑动窗口的长度，m 取值范围为 m = 1, 2, ..., N_w/2 1。

三、快速DAVAR的原理

DAVAR是一种基于逐点计算Allan方差的方法，用于定性分析信号中各类误差成分随时间的变化情况。由于需要在多个时间点上重复计算Allan方差，传统方法存在数据处理量大、运算效率低等问题。为此，本文介绍两种加速计算的策略，其中第二种方法尤其适用于Allan方差的高效求解，实际应用效果显著。

3.1 递归算法

DAVAR的核心思想是将长度为 N_w 的矩形窗沿信号 θ(t) 滑动，每次移动一个采样点。值得注意的是，相邻两个窗口之间有 (N_w1) 个数据点是重叠的。这意味着当前时刻的Allan方差可以在前一时刻计算结果的基础上进行更新，而无需完全重新计算。

为此，可将DAVAR公式重写为以下形式：

σ_A²[n, m] = 1/(2mτ) × 1/(N_w2m) × ∑_{k = nN_w/2}^n+N_w/22m1 Δ_m²[k]

其中，Δ_m[k] = θ[k+2m] 2θ[k+m] + θ[k]，表示二阶差分项。

定义差分序列如下：

Δ[k] = θ[k + 2m] 2θ[k + m] + θ[k]

基于此，下一时刻的动态Allan方差（DAVAR）可表示为：

σ[n + 1, m] = (1 / (2mτ)) × (1 / (N_w 2m)) × [∑_{k = n N_w/2}^{n + N_w/2 2m 1} Δ[k] + Δ[n + N_w/2 2m] Δ[n N_w/2]]

由上述表达式可进一步推导出递归形式的计算公式：

σ[n + 1, m] = σ[n, m] + (1 / (2mτ)) × (1 / (N_w 2m)) × (Δ[n + N_w/2 2m] Δ[n N_w/2])

由此可见，在从时间点 n 更新至 n+1 的过程中，只需在原有 σ[n, m] 的基础上，减去旧采样点 θ[n N_w/2] 对应的贡献项，并加入新进入窗口的采样点 θ[n + N_w/2 2m] 所带来的增量。该方法避免了重复全量计算，显著降低了 DAVAR 的运算复杂度。

关于相关时间 τ 的选取策略，通常设定为 τ = mτ，即在原始线性尺度下等间隔采样。然而，由于 Allan 方差图常采用双对数坐标（log-log），若 τ 仍保持线性分布，则在对数轴上其分布将变得密集，尤其在大 τ 区间内，导致计算资源浪费且对图形趋势描绘贡献有限。

考虑到 DAVAR 主要用于定性分析信号随时间变化的趋势，在不牺牲估计精度的前提下，可优化 τ 序列的选择方式，使其在对数域中近似均匀分布，从而减少不必要的计算量。

为此，引入指数函数构造 τ 序列：

τ(i) = τ_con × τ_gⁱ¹，其中 i = 1, 2, 3, …

当 τ_g 固定时，随着 i 线性增长，τ(i) 在对数坐标系中呈现均匀分布特性。结合 Allan 方差的精度要求，设定估计误差不超过 25%，根据误差分析理论，需满足最小分组数条件：N / m_max ≥ 9，其中 m_max 表示最大延迟因子对应每组的样本数量。

由此可得最大相关时间约束：

τ_max = m_maxτ ≤ Nτ / 9

代入具体参数：N = 10000，τ_con = 1，i = 100，τ = 1s，解得 τ_g ≈ 1.073。该比值确保了 τ 序列在对数空间中的合理分布，兼顾计算效率与分析精度。

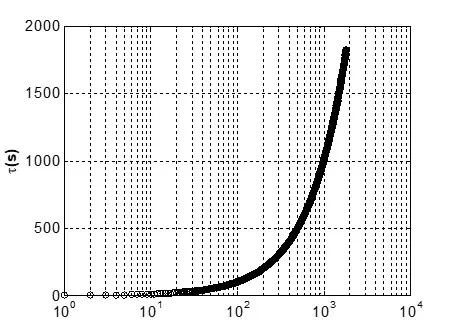
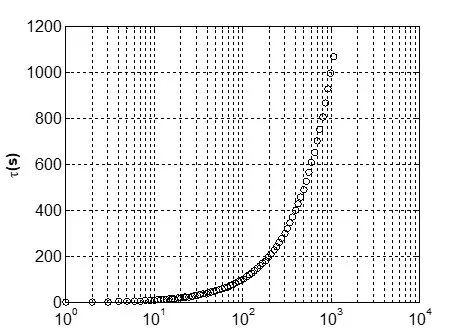
在对数坐标系中，序列

τ(i) = 1.073ⁱ¹（其中 i = 1, 2, 3, …, 99）

的分布情况如下图所示。可以看出，相关时间 τ 在对数尺度下呈现出较为均匀的分布特性。这种均匀性显著减少了 Allan 方差计算过程中的运算负担，尤其对于需要处理多组动态 Allan 方差（DAVAR）的应用场景，整体计算效率得以大幅提升。

四、相关代码实现

4.1 快速动态 Allan 算法主程序

tic
clear all
close all
h = waitbar(0, '正在运行->>>>>>');
N = 5555;
Half = floor(N / 2);
tau0 = 1;
flag = 1;
source = load('D:\XXX');
X = source.data;
nnn = length(X);
x = cumsum(X(1:nnn-1)');
t = 1:nnn-1;
Nx = length(x);
Nt = length(t);

if ~mod(N, 2)
    error('N must be odd');
end

% 参数初始化
Kmin = 5;          % 最小分组数量
i_max = 100;
temp_tau1 = zeros(i_max, 1);
Tr = nthroot(N / Kmin, i_max - 1);  % 计算根值

for i = 1:i_max
    temp_tau1(i) = floor(tau0 * Tr^(i - 1));
end

temp_tau2 = zeros(i_max, 1);
j = 1;
temp_tau2(1) = temp_tau1(1);

for i = 2:i_max
    if temp_tau1(i) ~= temp_tau1(i-1)
        j = j + 1;
        temp_tau2(j) = temp_tau1(i);
    end
end

nn = j;
tau = zeros(nn, 1);

for i = 1:nn
    tau(i) = temp_tau2(i);   % 确定最终的时间间隔序列
end

% 初始化输出变量
min2 = zeros(nn, 1);
max2 = zeros(nn, 1);
sigma2 = zeros(nn, 1);
S = zeros(nn, Nt - N);

% 滑动窗口计算 Allan 方差
for n = Half + 1 : Nt - Half
    xN = x(n - Half : n + Half);
    
    if (n - Half) == 1
        [S(:, n - Half), sigma2, min2] = allan_use_for_fast_fast(xN, tau);
    else
        next_sigma2 = sigma2;
        next_min2 = min2;
        [S(:, n - Half), sigma2, min2] = allan_fast_fast(xN, next_sigma2, next_min2, tau);
    end
    
    waitbar((n - Half) / (Nt - N), h);
end

% 可视化结果
if flag && Nt > 1
    figure;
    mesh(t(Half+1:Nt-Half)-2778, tau, S);
    set(gca, 'YDir', 'reverse', 'YScale', 'log', 'ZScale', 'log');
    V = [0, 1744, 0, 1000, 3.706317630769962e-003, 0.1];
    axis(V);
    xlabel('t(s)', 'fontweight', 'bold'); set(get(gca,'Xlabel'), 'FontSize', 12);
    ylabel('\tau(s)', 'fontweight', 'bold'); set(get(gca,'Ylabel'), 'FontSize', 14);
    zlabel('\sigma(t,\tau)', 'fontweight', 'bold'); set(get(gca,'Zlabel'), 'FontSize', 14);
    hidden off;
    view(-73, 28);
    close(h);
end

figure;
plot(X(Half+1:Nt-Half)); grid on;
set(gca, 'FontSize', 12);
xlabel('time(s)', 'fontweight', 'bold'); set(get(gca,'Xlabel'), 'FontSize', 12);
ylabel('random error((°)/h)', 'fontweight', 'bold'); set(get(gca,'Ylabel'), 'FontSize', 12);
toc

4.2 子函数一：Allan 偏差基础计算函数

该子函数用于初始状态下的 Allan 偏差计算，主要完成累加和统计量的初始化工作。

% Allan Deviation
function [sigma, temp_sigma2, temp_min2] = allan_use_for_fast_fast(x, tau)

N = length(x);
taumax = length(tau);
temp_sigma2 = zeros(taumax, 1);
sigma = zeros(taumax, 1);
temp_min2 = zeros(taumax, 1);

for k = 1:taumax
    n = 1;
    temp_min2(k) = (x(n + 2*tau(k)) - 2*x(n + tau(k)) + x(n))^2;
    
    for n = 1:N - 2*tau(k)
        temp_sigma2(k) = temp_sigma2(k) + (x(n + 2*tau(k)) - 2*x(n + tau(k)) + x(n))^2;
    end
    
    temp_sigma2(k) = 1/(2*tau(k)^2) * 1/(N - 2*tau(k)) * temp_sigma2(k);
    temp_min2(k) = 1/(2*tau(k)^2) * 1/(N - 2*tau(k)) * temp_min2(k);
    sigma(k) = sqrt(temp_sigma2(k));
end

sigma = sigma';

4.3 子函数2

function [sigma, temp_sigma2, temp_min2] = allan_fast_fast(x, sigma2, min2, tau)

N = length(x);
taumax = length(tau);
temp_min2 = zeros(taumax, 1);
max2 = zeros(taumax, 1);
sigma = zeros(taumax, 1);
temp_sigma2 = zeros(taumax, 1);

for k = 1:taumax
    n = 1;
    temp_min2(k) = (x(n + 2*tau(k)) - 2*x(n + tau(k)) + x(n))^2;
    
    n = N - 2*tau(k);
    max2(k) = (x(n + 2*tau(k)) - 2*x(n + tau(k)) + x(n))^2;
    
    temp_min2(k) = 1/(2*tau(k)^2) * 1/(N - 2*tau(k)) * temp_min2(k);
    max2(k) = 1/(2*tau(k)^2) * 1/(N - 2*tau(k)) * max2(k);
    
    temp_sigma2(k) = sigma2(k) - min2(k) + max2(k);
    sigma(k) = sqrt(temp_sigma2(k));
end

sigma = sigma';

总结

DAVAR 方法在分析陀螺输出数据方面具有较强的直观性和有效性，能够有效识别并分离信号中包含的主要随机误差成分，从而对陀螺仪的性能进行客观评估。然而，由于该方法需要对信号在各个时间点上的 Allan 方差进行估计，导致整体计算量较大，运算耗时较长。

为解决这一问题，本文引入了递推算法以及基于选择特定相关时间的优化策略，显著提升了计算效率，大幅缩短了 DAVAR 的运算时间。这种改进后的方案在处理大规模数据时表现优异，同时适用于计算资源和电源受限的移动设备，具备良好的应用潜力与推广价值。

扫码加我拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

前言