1、前提条件

确保已配置好 Python 开发环境，并安装后续实验所需的相关库，包括但不限于：numpy、scikit-learn、Keras、TensorFlow、PyTorch、matplotlib 以及 OpenCV 等常用科学计算与深度学习工具包。

2、可视化预测图展示

3、结果分析

本实验利用一个结构简单的神经网络完成对非线性函数的拟合任务，通过图表全面展现训练过程及最终拟合效果。以下是对图中关键元素和核心逻辑的详细解析：

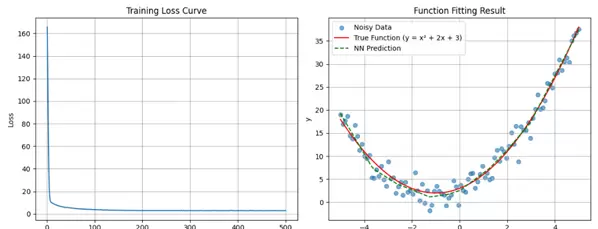
左侧：训练损失曲线（Training Loss Curve）
横轴“Epoch”表示训练过程中迭代的轮次，范围为0到500；纵轴“Loss”反映模型预测值与真实值之间的误差程度。初始阶段损失值较高，随着训练推进迅速下降，在约50个训练周期后趋于接近零并保持稳定。这一趋势清晰地表明模型已逐步收敛——在反向传播机制驱动下，网络参数不断优化，有效学习到了数据中的潜在规律。

右侧：函数拟合效果图（Function Fitting Result）
图中包含三类关键标识：
- 蓝色圆点标记为“NOISY DATA”，代表含有随机噪声的训练样本，由真实函数叠加扰动生成；
- 红色实线标注为“True Function”，对应目标函数表达式 \( y = x^2 + 2x + 3 \)，是一条标准的二次抛物线，体现典型的非线性关系；
- 绿色虚线显示为“NN Prediction”，即神经网络输出的预测结果。该曲线与红色真实函数几乎完全重合，且良好覆盖了带噪声的数据点，说明模型具备出色的去噪能力和泛化性能。

尽管所用神经网络结构简洁，但其展现出强大的非线性拟合能力。训练过程中损失快速下降，验证了参数更新策略的有效性；在预测阶段，模型能精准还原二次函数的整体形态，即使输入数据存在干扰，依然能够剥离噪声、逼近真实函数的本质规律。

整幅可视化图表设计清晰直观，采用“训练轮次-损失变化”与“数据样本-真实函数-预测输出”的双维度呈现方式，完整验证了简单神经网络在学习输入与输出之间复杂映射关系方面的基本原理与实际效能。

4、实现代码

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader

# 设置随机种子，保证结果可复现
np.random.seed(42)
torch.manual_seed(42)

# 1. 生成一元二次函数数据 y = x? + 2x + 3 + 噪声
# 生成-5到5之间的100个数据点
x = np.linspace(-5, 5, 100)
# 真实函数关系
y_true = x ** 2 + 2 * x + 3
# 添加高斯噪声，使数据更接近真实场景
noise = np.random.normal(0, 2, size=y_true.shape)  # 均值0，标准差2的噪声
y = y_true + noise

# 转换为PyTorch张量，并添加批次维度
x_tensor = torch.FloatTensor(x).view(-1, 1)  # 形状变为(100, 1)
y_tensor = torch.FloatTensor(y).view(-1, 1)  # 形状变为(100, 1)

# 创建数据集和数据加载器
dataset = TensorDataset(x_tensor, y_tensor)
dataloader = DataLoader(dataset, batch_size=10, shuffle=True)  # 批次大小10，打乱数据


# 2. 定义神经网络模型
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        # 定义两层神经网络：输入层(1) -> 隐藏层(16) -> 输出层(1)
        self.layers = nn.Sequential(
            nn.Linear(1, 16),  # 输入层到隐藏层
            nn.ReLU(),  # 激活函数，增加非线性能力
            nn.Linear(16, 1)  # 隐藏层到输出层
        )

    def forward(self, x):
        return self.layers(x)


# 3. 初始化模型、损失函数和优化器
model = SimpleNN()
criterion = nn.MSELoss()  # 均方误差损失，适合回归问题
optimizer = optim.Adam(model.parameters(), lr=0.01)  # Adam优化器，学习率0.01

# 4. 训练模型
epochs = 500  # 训练轮数
losses = []  # 记录每轮的损失值

for epoch in range(epochs):
    model.train()  # 设置为训练模式
    total_loss = 0

    for batch_x, batch_y in dataloader:
        # 前向传播：计算模型预测值
        outputs = model(batch_x)
        # 计算损失
        loss = criterion(outputs, batch_y)

        # 反向传播和优化
        optimizer.zero_grad()  # 清空上一轮的梯度
        loss.backward()  # 计算梯度
        optimizer.step()  # 更新参数

        total_loss += loss.item()

    # 计算平均损失并记录
    avg_loss = total_loss / len(dataloader)
    losses.append(avg_loss)

    # 每50轮打印一次训练信息
    if (epoch + 1) % 50 == 0:
        print(f'Epoch [{epoch + 1}/{epochs}], Loss: {avg_loss:.4f}')

# 5. 可视化训练过程
plt.figure(figsize=(12, 5))

# 绘制损失曲线
plt.subplot(1, 2, 1)
plt.plot(range(1, epochs + 1), losses)
plt.title('Training Loss Curve')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.grid(True)

# 6. 模型预测与结果可视化
model.eval()  # 设置为评估模式
with torch.no_grad():  # 不计算梯度，节省计算资源
    y_pred = model(x_tensor).numpy()  # 模型预测值

# 绘制拟合结果
plt.subplot(1, 2, 2)
plt.scatter(x, y, label='Noisy Data', alpha=0.6)  # 带噪声的数据点
plt.plot(x, y_true, 'r-', label='True Function (y = x? + 2x + 3)')  # 真实函数曲线
plt.plot(x, y_pred, 'g--', label='NN Prediction')  # 神经网络预测曲线
plt.title('Function Fitting Result')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

# 7. 结果分析
print("\n===== 结果分析 =====")
# 计算最终的均方误差
final_mse = criterion(torch.FloatTensor(y_pred), y_tensor).item()
print(f"最终均方误差: {final_mse:.4f}")

# 分析模型能力
if final_mse < 5:
    print("模型拟合效果良好，能够较好地捕捉二次函数的非线性关系")
elif final_mse < 10:
    print("模型有一定拟合能力，但精度还有提升空间")
else:
    print("模型拟合效果不佳，可能需要调整网络结构或训练参数")

# 分析过拟合情况
# 在这个简单问题中，我们通过观察拟合曲线与真实曲线的一致性来判断
print("\n模型能够较好地拟合二次函数的弯曲特性，说明神经网络的非线性能力发挥了作用")
print("隐藏层的ReLU激活函数帮助模型学习了非线性关系，使简单的两层网络能够拟合二次函数")